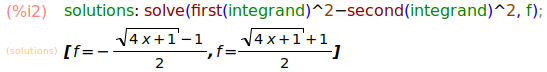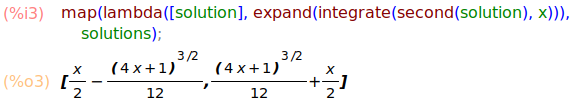Maxima 手習い（Maxima で積分）

ずっと以前から数式処理ソフトには憧れがあったのですが面倒臭そうなイメージがあってあまり調べてはいませんでした。
もう微分積分の計算方法を忘れつつあるので、せめて計算機で積分を計算できるように、やりかたを調べておこうと思いました。

お題はこんな積分です。

\int \sqrt{x + \sqrt{x + \sqrt{x + ...}}} dx

被積分関数を f とすると、上記の ... の部分もまた f と同じになるので

f = \sqrt{x + f}

と書けるはずです。Maxima でも同じく被積分関数を定義してみます:

integrand: f = sqrt(x + f);

wxMaxima で実行すると、数式を綺麗に表示してくれます。

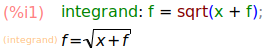
根号があると気持ち良くないので、この両辺を二乗して全体を ... = 0 の形の式に直すと:

f^2 - x - f

と変形できます。maxima 上でも、被積分関数の左辺 first(integrand) と 右辺 second(integrand) それぞれの二乗の差をとる式変形を以下のように書けます:

first(integrand)^2-second(integrand)^2

soluve を使って、この二次方程式の解を得ることができます。これで非積分関数 f を x の関数として得ることができました。

solutions: solve(first(integrand)^2-second(integrand)^2, f);

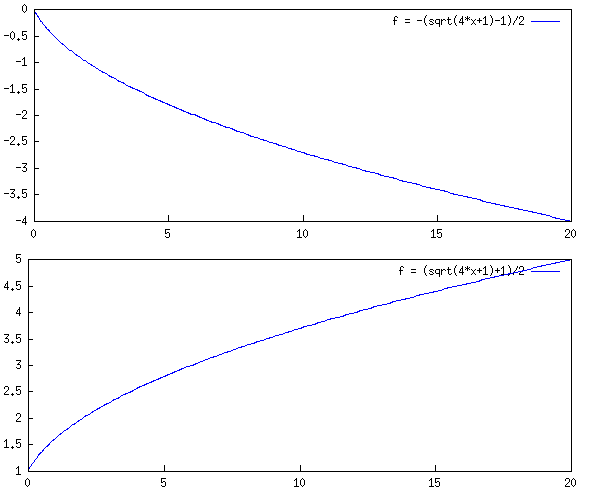
ラベルを solutions と複数形にしているのは、二次方程式の２つの解が結果として得られるためです。以下のようにプロットして見ると一方は x > 0 のときに負の値をとるので前者は不適格なのだろうと思うことができますが、リスト上から不適格な解を取り除く方法を知らない Maxima 初心者なのでこのまま計算を進めることにします...

draw(map(lambda([solution], gr2d(key=string(solution), explicit(second(solution), x, 0, 20))),
         solutions));

得られた２つの解それぞれを x で積分してみます。

map(lambda([solution], expand(integrate(second(solution), x))),
    solutions);

後者の結果が求めたい計算結果となりました。

手順をまとめて書くと、以下です:

integrand: f = sqrt(x + f);
solutions: solve(first(integrand)^2-second(integrand)^2, f);
map(lambda([solution], expand(integrate(second(solution), x))),
    solutions);