ライフゲームの連続値化の試み

はじめに

ライフゲーム（以下、LIFE と略）は培養基の中のバクテリアのような生命の増殖パターンを模して作られました。

過疎・過密だと死滅、適当な数の生存セルに隣接していると生存し続けられる、あるいは新たな生命が誕生する、というルールです。

「生」・「死」というのは一つのセルに一つの生命がある、という考え方ですが、これを「0」から「1」までの連続値にすれば集団の過密・過疎の興亡を表現できるかもしれないと思いました。

そこで、セルの値を「0」、「1」から「0」から「1」までの連続値にしたセル・オートマトンに拡張してみます。また、パラメータを変えることでコンウェイの LIFE を再現可能にできるようにもします。

離散ルールを元にした連続ルールの作成

コンウェイの LIFE 更新ルール

まず、コンウェイの LIFE の更新ルールを表に書き直してみます。

生きているセルの値を 1、死んでいるセルの値を 0、とするなら、
隣接する生きたセルの数＝隣接セルの値の総和
とすることができます。

隣接セルの値の和	0	1	2	3	4	5	6	7	8
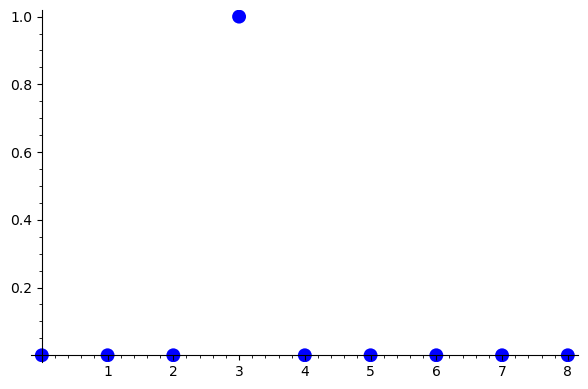
死んでいる(0)セルの次ステップでの状態	0	0	0	1	0	0	0	0	0
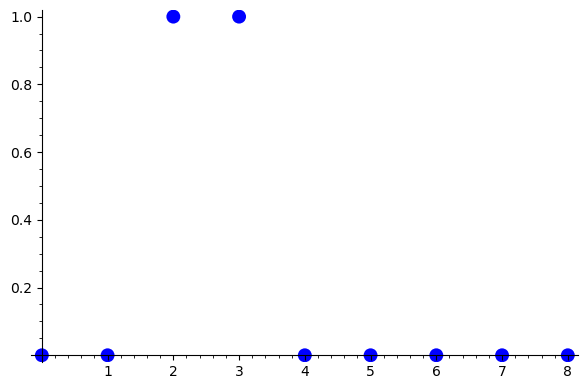
生きている(1)セルの次ステップでの状態	0	0	1	1	0	0	0	0	0

隣接セル値の和を x 軸に、次ステップでの状態を y 軸にして上記ルールをプロットすると：

関数を使った LIFE ルールの表現

まずは、上記ルールを関数で表現することを考えます。

まず、以下のような階段形状の関数（符号関数） $f$ があるものとします:

$$
f(x) = \begin{cases}
1 & (x > 0) \\
-1 & (x < 0)
\end{cases}
$$

（少なくともここでの議論では、x = 0 のときの値は -1 から 1 までの間にあればなんでも構いません）。

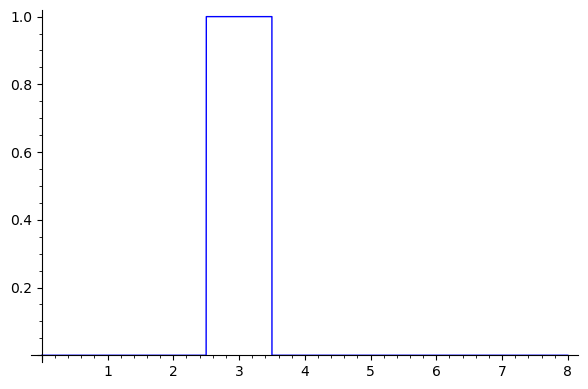
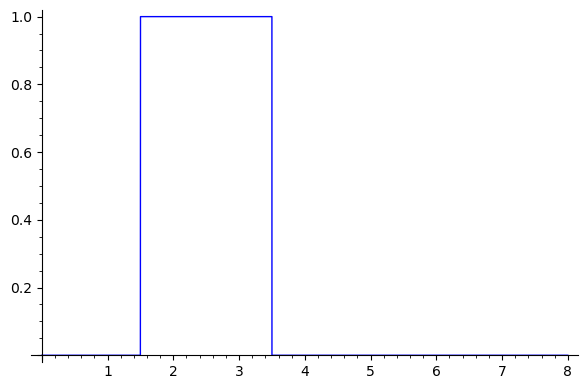
このような関数 $f$ があるなら、上記の矩形を以下のように書くことができます。

$$
C_{次} = \frac{1}{2} \times [ f(x - a) \times f(b - x) + 1 ]
$$

ここで、

• $x$ は隣接セルの値の和
• $C_{次}$ は当該セルの次ステップの値
• $a$ は当該セルの値に応じて 1 から 2 までの間、あるいは 2 から 3 までの間の適当な値を取る
• $b$ は 3 から 4 までの間の適当な値

ここで、「1 から 2 まで」などといったあいまいな書き方をしているのは、LIFE のルールはあくまで整数に対してのみ与えられているために恣意性があるためです。あまり深く考えていないのですが、中点の値でよいと思っています。

例えば、$a$ が 1.5（値 1 と 2 の間の中点）あるいは 2.5（値 2 と 3 の間の中点）を取るとするならば、当該セルの値 $C_{現在}$ （0 から 1 までの値をとる）に対して

$a = 2.5 - C_{現在}$

とすることができます。

これで、LIFE の次ステップセル値を決定する関数を得ることができました。

関数の鈍化による連続値 LIFE ルール

上記関数に使っている符号関数 $f$ を滑らかな関数で置き換えることを考えます。

• 単調増加である
• $x > 0$ のときに $f(x)$ の値は +1 以下の正の値である
• $x < 0$ のときに $f(x)$ の値は -1 以上の負の値である
• $x \rightarrow \infty $ のときの $f(x)$ の極限値は +1 である
• $x \rightarrow \infty $ のときの $f(x)$ の極限値は -1 である

ような関数がよいでしょう。

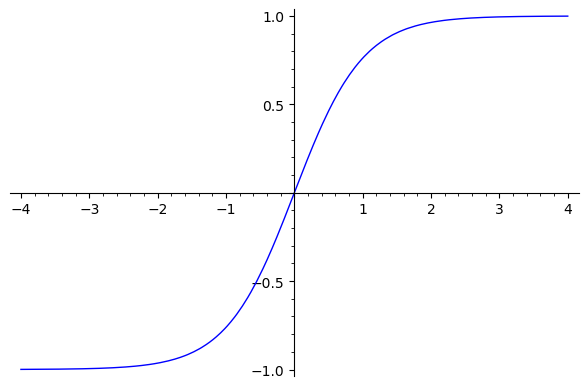
シグモイドとしては、Python の math モジュールにもあって使いやすかった $\tanh$ を使うことにします。

さらに、$f(x)$ に、どのくらい矩形に近いか（シャープか）を表すパラメータ $s$ を付与した関数 $f_s(x)$ を以下のように定義します:

$$
f_s(x) = \tanh (s x)
$$

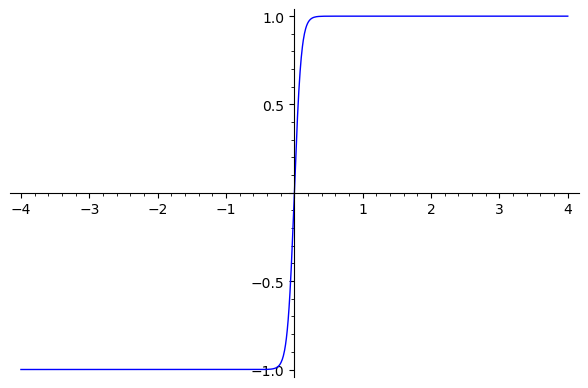
$s$ →∞ の極限で、$f_s(x)$ は階段関数 $f(x)$ とほぼ同じになります。

$s=10$ のときの $f_s(x)$ をプロットしてみると、こんな感じです:

上に書いたルールでの $f(x)$ を単純に $f_s(x)$ に置き換えると、ルールがどの程度 LIFE に近いか・遠いかをパラメータ $s$ で操作できるルールを得ることができます:

$$
C_{次} = \frac{1}{2} \times [ f_s(x - a) \times f_s(b - x) + 1]
$$

$$
\begin{array}{l}
a = 2.5 - C_{現在} \\
b = 3.5 \\
x は隣接セル上の値 C_{現在} の和
\end{array}
$$

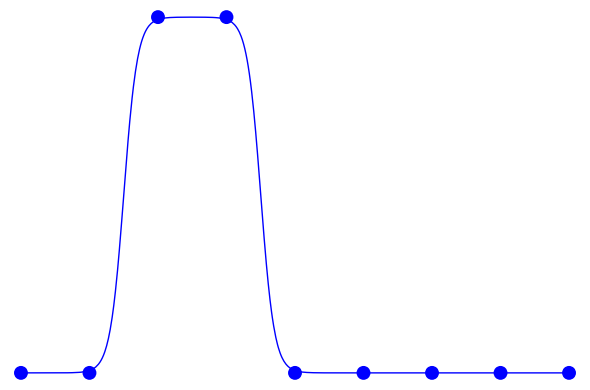
$ s \rightarrow \infty $　のときはオリジナルの LIFE のルールの矩形を再現します。

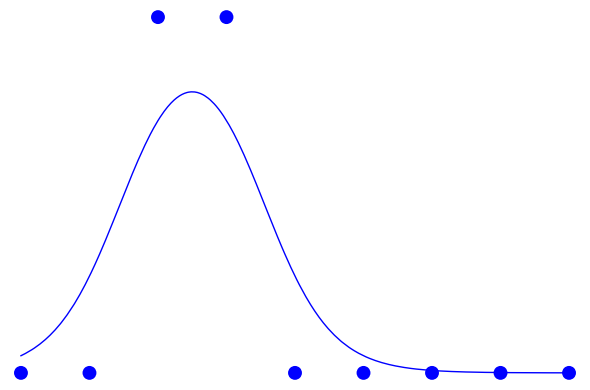
$s=5$ の場合を、オリジナルの LIFE のルール（ドットで示した部分）と比較するとこんな感じです:

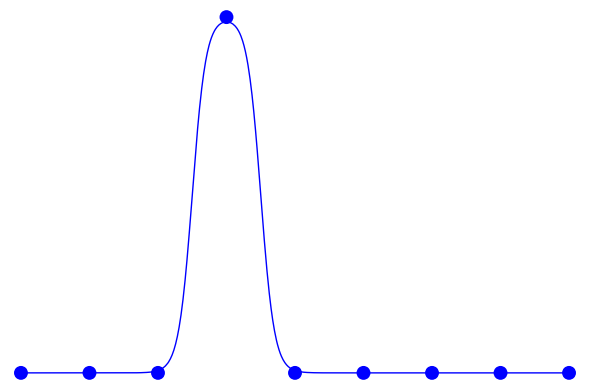
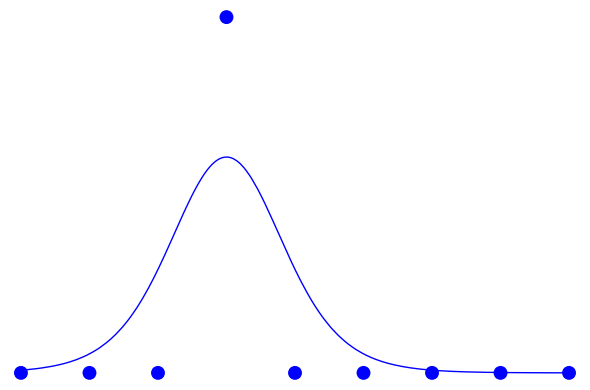
$s=1$ だとかなりなまってきて:

と、オリジナルの LIFE に比べるとピークの位置が下がってきます。下がってくる、というのはつまりこのルールではセルの値は 0 から 1 までの範囲より狭い範囲の値しかとらない、ということです。全体に適当な数を乗算してピークの位置を 1 に戻す、ということも考えられますが、これ以上ルールを複雑化するのもどうかと思われるのでこのままにしておきます。

実際シミュレーションを実行してみるとそれほど結果に違和感はありませんでした。

真空

空間を満たす全セルの値が同一かつ恒久的に変わらないとき、その状態を「真空」と呼ぶことにします。

通常の LIFE では真空状態のセルの値は０（死）です。パターンの変化を考えている以外の空間については全セルの値は 0 と考えることができます。

それに対し、上記で与えたルールでは全セルの値 0 は安定した状態ではないため、パターンの変化を考えている以外の空間の値を単純に 0 とおくことができません。

具体的には、全セルが

$
C_{真空} = \frac{1}{2} \times [ f_s(8 C_{真空} - (2.5 - C_{真空})) \times f_s(b - 8 C_{真空}) + 1]
$

を満たす値 $C_{真空}$ を取るときに安定します。
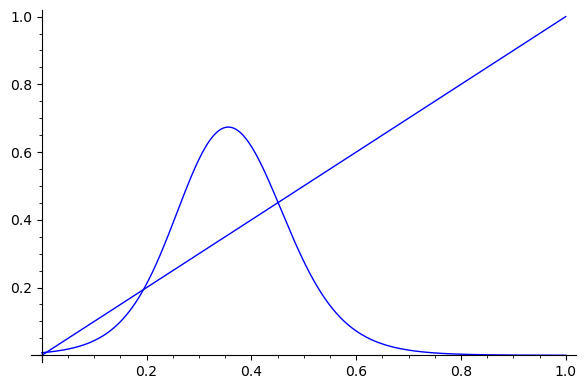
この値は「連続化したルールのもとでは、過疎にも過密にもならない密度が存在する」ということを示しています。

上のグラフのとおり、真空状態の候補（グラフの交点）は複数ありますが、最も値の小さい、最も 0 に近い値を「なにもない空間でのセルの値」として用いるのが一番扱いやすいだろうと思います。また、今回のルールでは最小の値のみが吸引的不動点で、それ以外は不安定で真空状態として扱うには不適当でした。

シミュレーションでは、予め真空状態のセルの値を計算しておくことで、真空セルの塊に関する次状態の計算を避ける、といった使い方が可能です。

シミュレーション

今回作成した連続化ルールについてパラメータ $s$ を下げていってみると、こんな感じの挙動でした:

• $s > 5$ : コンウェイの LIFE と全く同じ
• $s \sim 4$ : 一見 LIFE と同じ挙動に見えるが、誤差があるような微妙に違う動きをする
• $s \sim 3$ : グライダーの自然発生が滅多に見られなくなる、絶え間なく移動する紐状のものの集団が成長していく
• $s \sim 2$ : 絶え間なく移動する紐状のものの集団が成長していく
• $s \sim 1$ : LIFE の面影が完全になくなり、変化し続けるまだら模様の丸い塊が成長していく

どんぐり(Acorn)を初期状態として 100 ステップ計算したあとの状態を、それぞれの $s$ について示すと以下です：

$s = 5$

$s = 4$

$s = 3$

$s = 2$

$s = 1$

紐状のものはおそらく「過疎・過密」による淘汰に起因するドーナツ化現象が重なり合いつつ起きることで見えているのだと思います。
$s \sim 1$ でのまだら模様は、紐が更に平滑化された結果と思われます。

面白いのは、紐状の構造は必ずループとなっていることです。$s \sim 3$ で挙動を見ていると、点状の塊がドーナツ化し、そのドーナツが大きくなってループ状になり、ループがある程度成長したところで壊死による切れ目ができて複数の点状の塊あるいは新しい小さいループができる、といった感じに見えます。

ループが成長する様子は簡単にそのまま大きくなるわけでなく、部分的に大きくなったり小さくなったり消えていったりと非常に複雑です。この複雑さは LIFE っぽさを感じます。しかし、大局的には紐状のものが空間全体を覆い尽くしていく感じで LIFE に比べると面白くなくなった感じがあります。

まとめ

コンウェイの LIFE を元に、連続値を持つセル・オートマトンを作りました。

単一パラメータ操作により、コンウェイの LIFE を再現することも可能としました。

おまけ

シミュレーションの核となる部分を Python で書きました。
cells は座標 (x, y) を表すタプルをキーとして、その座標の float セル値を値として持つ辞書です。

def sig(x: float) -> float:
    u'''シグモイド'''
    return np.tanh(x)

def rect(sharpness: float, a: float, b: float, x: float) -> float:
    u'''a < x < b のときに 1 に近い値を、それ以外のときに 0 に近い値を返す'''
    return 0.5 * (sig(sharpness * (x - a)) * sig(sharpness * (b - x)) + 1)

def sum_neighbours(cells: Dict[Tuple[int, int], float],
                   point: Tuple[int, int],
                   vaccum_value: float) -> float:
    u'''隣接セルの和'''
    (x, y) = point
    return sum([cells.get(p, vaccum_value)
                for p in [(x + i, y + j)
                          for i in range(-1, 2)
                          for j in range(-1, 2)
                          if i != 0 or j != 0]])

def next_cell_value(cells: Dict[Tuple[int, int], float],
                    sharpness: float,
                    point: Tuple[int, int],
                    vaccum_value: float) -> float:
    u'''位置 point における次ステップのセルの値を返す'''
    sum = sum_neighbours(cells, point, vaccum_value)
    a = 2.5 - cells.get(point, vaccum_value)
    b = 3.5
    return rect(sharpness, a, b, sum)

def estimate_vaccum_value(sharpness: float, loop: int = 100) -> float:
    u'''真空セルの値を返す'''
    v = 0.0
    for i in range(loop):
        a = 2.5 - v
        b = 3.5
        v = rect(sharpness, a, b, 8 * v)
    return v

def life(cells: Dict[Tuple[int, int], float],
         sharpness: float,
         vaccum_value: float,
         epsilon: float) -> Dict[Tuple[int, int], float]:
    u'''全セルの次ステップ状態を返す'''
    return dict([
        (p, v)
        for (p, v) in [
                (point, next_cell_value(cells, sharpness, point, vaccum_value))
                for point in set([(x + i, y + j)
                                  for (x, y) in cells.keys()
                                  for i in range(-1, 2)
                                  for j in range(-1, 2)])]
        if (v > vaccum_value + epsilon or
            v < vaccum_value - epsilon)])