ベイズ推論(解析的手法)を用いたベルヌーイ分布の学習と予測

はじめに

当記事は講談社発行の「ベイズ推論による機械学習入門」のP.76からの例題を理解するためにPythonでコーディングしたものです

詳しく知りたい方はぜひ同書籍を購入してみてください

通常は・・・

こういったベイズ推論はStan、Edwardなどの確率的プログラミング言語を用い、MCMCを使って推論することが一般的かと思います

ここではそういった手法を使わず、ベイズ推論を理解するため数式ベースの解析的手法でこれを解いてみようかと思います

問題

ベルヌーイ分布、つまり０，１をとる確率分布の事後分布を予測したいと思います
ベルヌーイ分布は下記のようにコインの裏表をあらわすような、２値の値をとる確率分布ですね
ここでいう予測というのはデータXを与えて、μを推測することになります

x \in \{ 0, 1 \}　　\\
p(x | μ) = Bern(x | μ)

パラメータの学習

数式による解説

※簡易的な説明のみになります。詳しい内容は是非書籍をお買い求め下さい
※途中の数式は難しいですし（間違っているかもしれませんので）、pythonコードは非常に簡単なので、数式が苦手な方はコードだけ読んで下さい

予測したいパラメータμは０〜１の値が候補となります。
そのためμは、同じく０〜１を生成する確率分布であるベータ分布に従うことが予想されます

μ \in ( 0, 1 )　\\
p(μ) = Beta(μ | a, b)

ベルヌーイ分布とベータ分布をベイズ推論に当てはめて変換していきましょう
ちなみに総乗がベルヌーイ分布で、右側がベータ分布にあたります

\begin{eqnarray}
p(μ| X) &=& \frac{p(Y | X) p(X)}{p(Y)} \\
&\propto& \{\prod_{n=1}^{N} p(x|μ) \}p(μ)
\end{eqnarray}

このままでは計算しにくいので対数を取ります

\begin{eqnarray}
\ln{p(μ| X)} &=& \sum_{n=1}^{N}\ln{p(x|μ)} + \ln{p(μ)} + const.
\end{eqnarray}

この数式にベルヌーイ分布とベータ分布の対数変換したものを代入します
それぞれ対数をとると以下のように変換できるかと思います

\begin{eqnarray}
\ln{Bern(x | μ)} &=& x \ln{μ} + (1-x)\ln{(1-μ)} \\
\ln{Beta(μ | a, b)} &=& (a-1)\ln{μ} + (b-1)\ln{(1-μ)} + const.
\end{eqnarray}

これを代入して整理すると以下のようになります

\begin{eqnarray}
\ln{p(μ| X)} &=&  \sum_{n=1}^{N} x_n \ln{μ} + \sum_{n=1}^{N}(1-x_n)\ln{(1-μ)} + (a-1)\ln{μ} + (b-1)\ln{(1-μ)} + const. \\
 &=&  (\sum_{n=1}^{N}x_n + a - 1)\ln{μ} + (N -
 \sum_{n=1}^{N}x_n + b - 1)\ln{(1-μ)} + const.
\end{eqnarray}

この数式と、その上にあるベータ分布の数式を比較すると同じ構成していますね。
つまりここで取得できる事後分布はベータ分布となることがわかります
いわゆる共役事前分布というやつでベルヌーイ分布とベータ分布をかけると、ベータ分布になるという例のアレです

以上からベルヌーイ分布のμを表すベータ分布を予測する、つまりベータ分布のハイパーパラメータa,bを予測するためには以下でできることがわかります

\begin{eqnarray}
\hat{a} &=& \sum_{n=1}^{N}x_n + a \\
\hat{b} &=& N - \sum_{n=1}^{N}x_n + b \\
\end{eqnarray}

データXは今まで試行したもののち１が出た回数が格納されています
つまり推測とはいっても単に１が出た回数を保存しているだけになっています

pythonによる実装

さて長々と数式を書いてはきていましたが、やはりこれではわかりにくいのでpythonコードに落としていきましょう

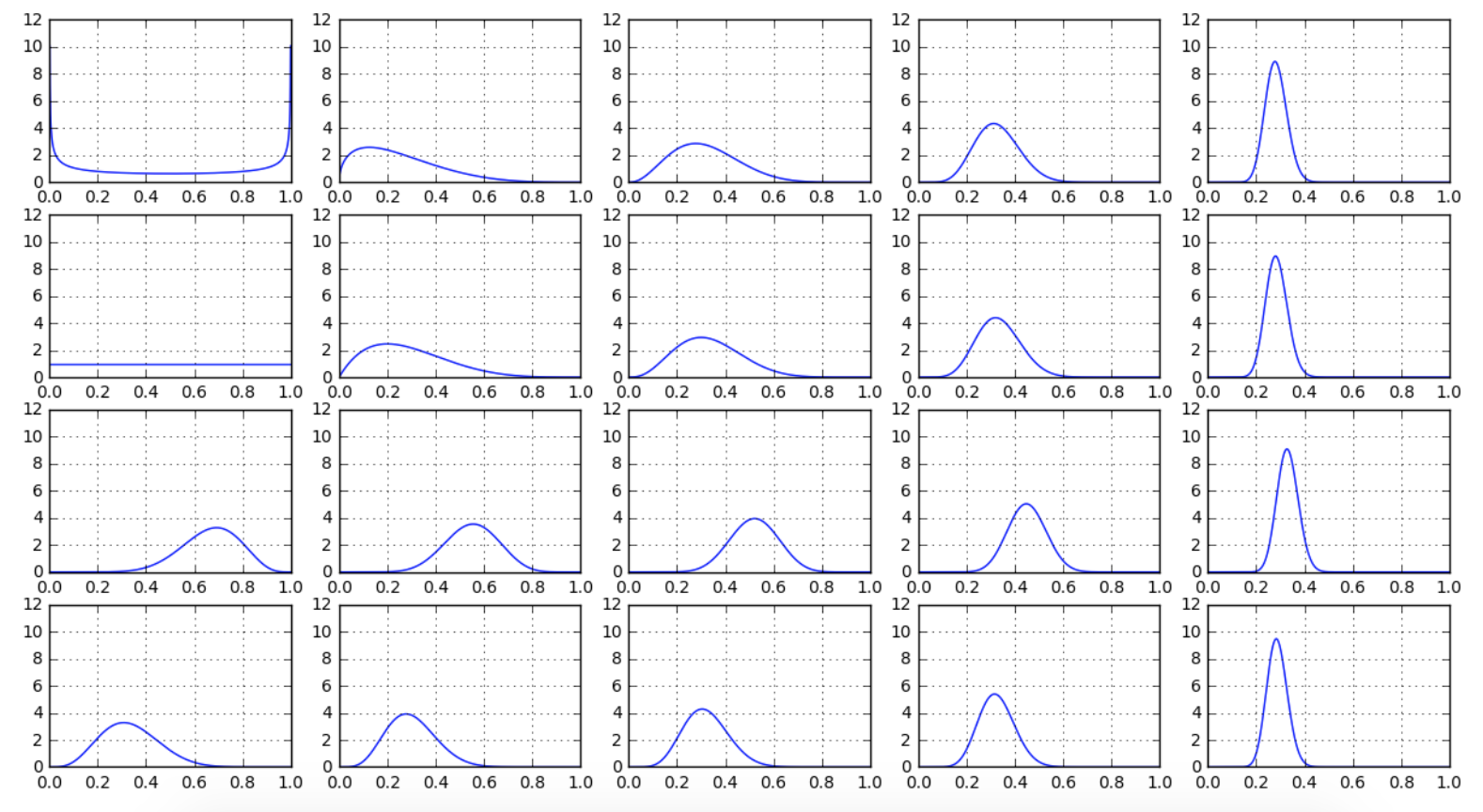
ここでは複数のベータ分布の初期パラメータから、0,5,10,25,100回試行した場合にこれがどうなるか見てみます

import numpy as np
import scipy.stats
from matplotlib import pyplot as plt

# ベルヌーイ分布に基づいた乱数発生（5,10,25,100回試行）
# 0が出た回数だけカウントする
b_5 = sum(filter(lambda n:n%2==1, bernoulli.rvs(0.25, size=5)))
b_10 = sum(filter(lambda n:n%2==1, bernoulli.rvs(0.25, size=10)))
b_25 = sum(filter(lambda n:n%2==1, bernoulli.rvs(0.25, size=25)))
b_100 = sum(filter(lambda n:n%2==1, bernoulli.rvs(0.25, size=100)))

# ベータ分布の初期値リスト
init_params = [ 
                   [0.5, 0.5]
                  ,[1.0, 1.0]
                  ,[10.0, 5.0]
                  ,[5.0, 10.0]
                 ]

# ベータ分布に与える事後確率用のa,bの値
params = [ 
                   [0, 0]
                  ,[b_5, 5-b_5]
                  ,[b_10, 10-b_10]
                  ,[b_25, 25-b_25]
                  ,[b_100, 100-b_100]
                 ]

# グラフ設定
# 　　　初期化
x = np.linspace(0, 1, 1000)
y_vals = []
# 　　　subplot設定
nrows = len(init_params)
ncols = len(params)
fig, axes = plt.subplots(nrows, ncols, figsize=(3*ncols, 2*nrows))

# 事後分布取得
# 初期値+回数ごとの事後確率値
for init_param in init_params:
    for param in params:
        rv = scipy.stats.beta(param[0]+init_param[0] ,param[1]+init_param[1])
        y = rv.pdf(x)
        y_vals.append(y)

# 表示
for ax, y in zip(axes.flat, y_vals):
    ax.set_ylim([0,12])
    ax.plot(x,y)
    ax.grid(True)

plt.show()

学習と呼ばれる部分は以下の足し算の箇所だけです

rv = scipy.stats.beta(param[0]+init_param[0] ,param[1]+init_param[1])

さて実行した結果は以下の通りとなります
どのパラメータから初めても結果がほぼ同じになり、学習機能が効果的に動いていることがわかりますね

予測

数式による解説

さてでは未知のデータを学習させて、ベルヌーイ分布μを予測してみましょう
予測の数式は途中課程がガンマ関数が乱発しており、非常にわかりにくいので詳しくは参考書籍を購入してご覧ください

予測自体は以下の数式で可能となります
ここで出て来るa,bは上記学習欄に出てくるベータ分布のa,bになります

\begin{eqnarray}
p (x_*|X) &=& Bern(x_* | \frac{\hat{a}}{\hat{a} + \hat{b}}) \\
&=& Bern(x_* | \frac{\sum_{n=1}^{N}x_n + a}{N + a + b})
\end{eqnarray}

pythonによる実装

さて実装です。
こでは複数のベータ分布の初期パラメータを使い、１０００回試行してそれぞれの場合のベルヌーイ分布のパラメータμを推測したいと思います

# ベルヌーイ分布にもとづき１０００回試行
b_1000 = sum(filter(lambda n:n%2==1, bernoulli.rvs(0.25, size=1000)))

# ベータ分布の初期値リスト
init_params = [ 
                   [0.5, 0.5]
                  ,[1.0, 1.0]
                  ,[10.0, 5.0]
                  ,[5.0, 10.0]
                 ]

# ベータ分布に与える事後確率用のa,bの値
param = [b_1000, 1000-b_1000]

# ベルヌーイ分布のパラメータμの推定
for init_param in init_params:
    mu = (param[0]+init_param[0] ) / (param[0]+init_param[0] + param[1]+init_param[1])
    print("ベータ分布の初期値: %s" % (init_param))
    print("       %s　 \n" % (mu))

結果は以下の通りとなります
想定値の０．２５にすべて近くなっており正しく予測できていることがわかります

ベータ分布の初期値: [0.5, 0.5]
       0.233266733267　 

ベータ分布の初期値: [1.0, 1.0]
       0.233532934132　 

ベータ分布の初期値: [10.0, 5.0]
       0.239408866995　 

ベータ分布の初期値: [5.0, 10.0]
       0.234482758621

最後に

次はポワソン分布で同じ事をしようかと