LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@tackey

論文まとめ：Distributed Representations of Web Browsing Sequences for Ad Targeting

Last updated at Posted at 2020-01-31
Page 1 of 30

はじめに

  • 元論文

  • PV-DM（doc2vec）をサイト内行動に応用している。のでPV-DMをわかってないとキツそう…

  • サイト内行動に関するドメイン知識をもとに改善している

    • データはYahoo!JAPAN。Yahoo!内でのユーザー行動ではある一連の行動において、ユーザーの興味関心は後半に色濃く出る（前半はYahoo!トップなど。それだけではユーザーの興味はわからない）。
    • そのドメイン知識を元に、後半のユーザー行動を重視するような手法にしている

  • PV-DMをサイト内行動に応用するにあたり、ページ来訪データとWikipediaのデータの分布の比較を行っている

  • 以下、論文のまとめです。なお、図等は原論文から引用させていただきました。

Abstract

あるユーザーの一連のURL遷移とURL1つをそれぞれ、パラグラフと単語と捉えて、ユーザーのページ来訪の流れを要約する。
（ユーザーの一連のURL遷移が文章（パラグラフ）、セッションが一文、URLが単語という位置付け）

ユーザー単位で要約したものは、ユーザー関連の予測タスクに用いることができる。
Paragrah Vectorの改善版、Backward PV-DMを紹介する。

1. Introduction

Paragraph Vector(doc2vec)

ユーザーのページ来訪について、ユーザーをパラグラフ、URLを単語と捉え、ベクトルモデルを当てはめた。

しかし、ページ来訪データは自然言語データと同様に扱っていいのだろうか。ページ来訪データとWikipediaデータ(English)の分布を比較する。

Main Contributions

  • ページ来訪とwikipediaの頻度分布における共通点と違いを述べる
  • 分析を元に、Backward PV-DMを提案する
  • 2つのY!データを元に、Backward PVDMや既存手法の評価を行う

2. User Activities on the Web

ユーザーごとのページ来訪をURL単位で見る。

$$(a_{i,1}, a_{i,2},..., a_{i,T_i})$$

↑ユーザーiのt番目の来訪ページが$a_{i,t}$

URLはハッシュ化されていても良いため、他企業からデータをもらった場合でも可能。（具体的なURLがわからなくても大丈夫ということだと思う）

URL以外にも、検索クエリや広告クリックにも拡張可能。

2.1 Data Analysis on Web Page Visits

Y!データの紹介

  • 2014年7月22日のデータ
  • アクセスログにはスマホ・タブレットアプリのログも含んでいる
  • 10ページから1000ページ来訪したユーザーに絞っている
  • 5回以上現れなかったURLは削除した
  • 30分以上間隔が空いた場合は別セッションとした
  • ユーザーごとのページ来訪はパラグラフないしdocument。その中の1sessionは1sentenceに該当する。（そして1URLはword）
  • 387万URL、10億ページ来訪。

wikipediaと比較した結果

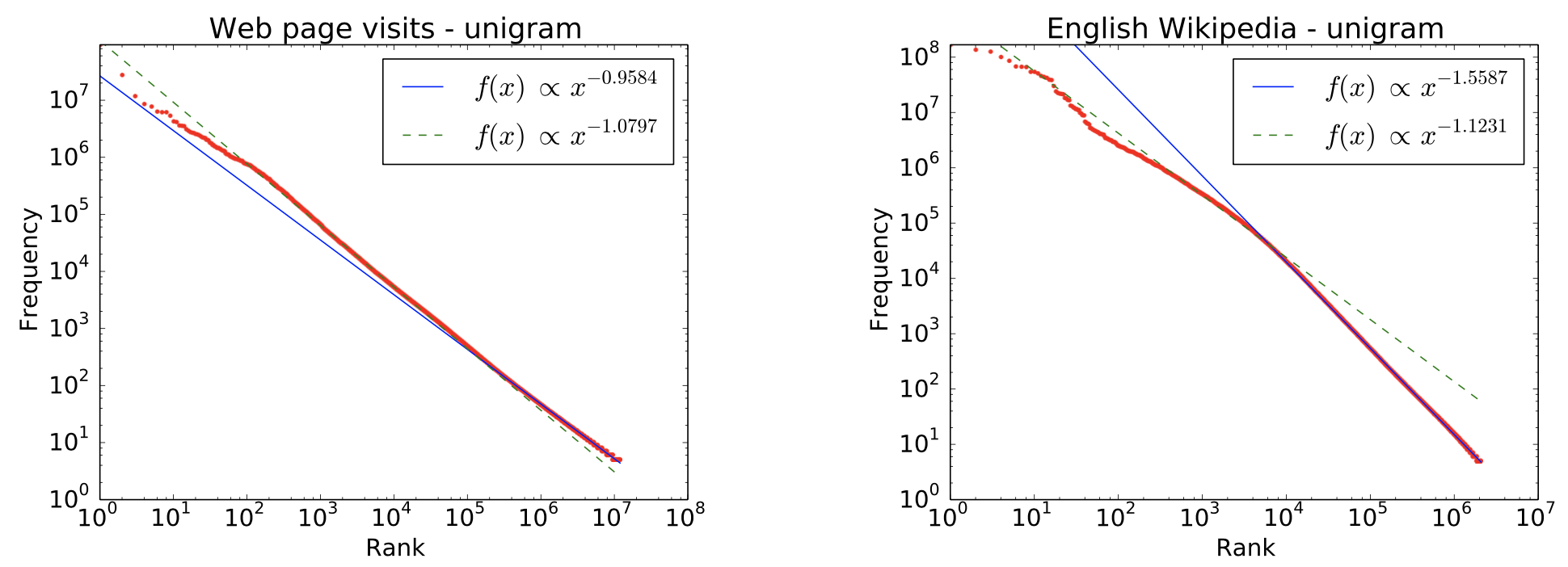
  • Y!データのURLごとの出現頻度はpower-law分布(冪乗則)。wikipediaも同様。
  • session(sentence)単位での相対位置に着目すると、Y!とwikipediaは大きく異なった。（あるURLがsessionの中での出やすい位置に傾向があるのに対し、ある単語は文章のなかで出やすい位置に傾向は）

出現頻度

  • log-log plotを見ると、概ね直線的。

image.png

  • 両方ともpower lawにしたがっていると言えるが、ページ来訪の方がtail（グラフの右の方）が太っている。（ページ来訪のURLの方がランキングが低いものでも出現回数が比較的多い）

相対位置の出現頻度

  • Y!データ：1sessionにおける後方のURL(ユーザーが1session中で最後の方に見たURL)はtailのURL(全体の中で件数が少ないURL)である。1sessionにおける前方のURLはheadのURL（全体の中で件数が多いURL）である。
  • wikipedia：1sentenceにおける出現頻度は概ね均等
  • Y!データはトップページから流入し、ハイパーリンクを辿って各ページにすすむ。ハイパーリンクか検索を使って興味あるページへすすむ。
  • ユーザーの興味関心を掴むには、sessionの後半に現れる、tail URL（出現頻度の少ないURL）が重要ということがわかった。
  • この分析のために用いた数式とそのグラフ
    $$\log \left(\frac{\operatorname{freq}\left(a_{i, t+k}\right)}{\operatorname{freq}\left(a_{i, t}\right)}\right)$$

image.png

  • この数式は下記のような計算だと思います
  • 例えば
    • 全ユーザーの全session中、URLのAが100回、Bが20回、Cが1回出現したとする
    • ある1セッションでA→B→Cと辿っていたとする。
    • $k=1$ (relative position)の時、
      • A→Bは $\log \left(\frac{\operatorname{freq}\left(B\right)}{\operatorname{freq}\left(A\right)}\right) = \log \frac{20}{100}$
      • B→Cは $\log \left(\frac{\operatorname{freq}\left(C\right)}{\operatorname{freq}\left(B\right)}\right) = \log \frac{1}{20}$
      • つまり$k=1$ のときは、出現回数が多いURLがセッションの中で初めの方に現れている時に負の値を取りやすくなる。

3. Existing Vector Models

既存手法のParagraph Vectorsやword2vecを用いた場合について紹介する。

Paragraph Vectors

  • PV-DM
  • PV-DBoW

word2vec

  • CBoW
  • Skip-gram

3.1 PV-DM(Distributed Memory Model of Paragraph Vectors)

  • ベクトルモデルの目的関数（下記を最大化したい）

$$\sum_{t} \log p\left(a_{i, t} | a_{i, t-1}, \ldots, a_{i, t-s}, u_{i}\right)$$

  • sessionごとに、「過去の」来訪URLとそのユーザー情報を元に、t時点の来訪URLを予測する。
  • sはcontext window(直近いくつ分の来訪URLを参照するか)
  • 予測はマルチクラスなので、softmaxを用いる

image.png

  • $w_{a_{i,t}}$ はoutput vector。
    • $v_I$ はinput vectorで、それまでの来訪URLとユーザー情報。
  • PV-DMはn-gramモデルとトピックモデルの組み合わせと考えられる
  • user vectorはuser-relatedな予測タスク（広告クリック予測）などの特徴量に用いることができる

3.2 PV-DBoW

Distributed Bag of Words version of Paragraph Vector

下記を最大化したい。

$$\sum_{t} \log p\left(a_{i, t} | u_{i}\right)$$

image.png

context-windowが0の、単純化されたPV-DMと言える

3.3 CBoW and Skip-gram

word vectorモデルについても触れる。

Paragraph Vectorと同様、log probabilitiesを最大化する点は同じ。

ただこれは行動（来訪URL）の表現を得ることができるが、userの表現を直接得ることができない。

CBOW

$$\sum_{t} \log p\left(a_{i, t} | a_{i, t-s}, \ldots, a_{i, t-1}, a_{i, t+1}, \ldots, a_{i, t+s}\right)$$

image.png

t時点の来訪URLを前後の来訪URLから予測する。

$V_I$はcontext vectorの平均。PV-DMとは異なる

Skip-gram

$$\sum_{t} \sum_{-s \leq k \leq s, k \neq 0} \log p\left(a_{i, t+k} | a_{i, t}\right)$$

ある時点の来訪URLを元に、前後の来訪URLを予測するように学習する。

Directed Skip-gram modelは、ある時点の来訪URLを元に未来の来訪URLを予測するモデル。(kが0より大きい値のみになっている)

$$\sum_{t} \sum_{0<k \leq s} \log p\left(a_{i, t+k} | a_{i, t}\right)$$

4. Proposed Method

今回の論文で提案するのはBackward PV-DM

4.1 Backward PV-DM

ここではPV-DMの修正版として

  • Reverse PV-DM
  • Backward PV-DM

の2つを紹介する。

image.png

PV-DMとの違いはcontext window。Reverse PV-DMとBackward PV-DMの条件つき確率は下記で一緒

$$\sum_{t} \log p\left(a_{i, t} | a_{i, t+1}, \ldots, a_{i, t+s}, u_{i}\right)$$

ある時点 t より未来の時点の来訪URLから、t時点の来訪URLを予測する。

Reverse PV-DMとBackward PV-DMの違い

Reverse PV-DMとBackward PV-DMの違いはcontext windowのSlidingする方向。

slidingする方向は最大化する目的関数を変えない。ただこの目的関数はbilinear formなのでconcave(凹)でない。(わからない…)
そのためslidingする方向を変えることで、より良い目的関数の最大となる場所を見つけることができる。（4.2で説明する）

slidingする方向（inputの順序）はuser vectorの質に影響を与える。

セッションの後方の来訪URLは有益なので、最後にinputすべき。

4.2 Learning the vector models

activityの種類数（URLの種類数）が大きいため、ここまでの式、一次導関数の計算が非現実的。

そこで、negative samplingのアプローチをとった。
(softmaxの代わりに用いる手法。多値分類だと計算コストがかかるため二値分類に変換する。)

目的関数

$$\log p\left(a_{i, t} | a_{i, t-1}, \dots, a_{i, t-s}, u_{i}\right)$$

の代替は式2（1か？）に伴い下記と定義される

image.png

  • σはシグモイド関数
  • kはランダムにサンプリングされたnegative instanceの数
  • $p_n(a)$ はnegative instanceを生成するnoise distribution
    • "unigram" distributionを用いた[10]
  • modelの学習には asynchronous SGDを用いた[13]。AdaGrad[7]も用いた。

新規ユーザーの推論(user vector $v_u$)をする際には、activityのinput vector $v_a$（各URLのベクトル）とoutput vector $w_a$（推論時に用いる行列）は固定する。

5. Experiments

実験にはY!JAPANのウェブサービスの2つのリアルデータを用いた

まとめると、

  • ある日のY!内での遷移を元に、翌日の広告クリック、広告主サイト来訪を予測するというタスクだと思う
  • 今回の提案手法等で特徴量を作成し、その特徴量を元にロジスティックリグレッションで上記タスクを解く
  • 評価はAUC
  • 正例はクリックした人・サイト来訪した人だと思うが、負例はどうやって選んだのかわからない…

5.1 Data sets

AdClicker : 5つの広告キャンペーンのコンテンツ連動型広告をクリックしたユーザーのデータ（Y!内での遷移？）
SiteVisitor : 5つの広告主のウェブサイトの来訪ユーザーからなるデータ（Y!内での遷移？）
(クリックした人よりサイト来訪者の方が多くなるのはそれはそう。)

image.png

※ Featuresは5回以上データセットに現れたURLの件数。

TrainとValidationデータは2014/7/22,23のデータを用いた。
22日のURL履歴から23日の特定の行動を予測する。（22日のデータがfeatureで、23日のデータがラベル）

Testには7/23,24のデータを用いた。
Y!Jのログは、ユーザーのウェブ上での行動での一部分に過ぎない。
featureには広告主サイトの来訪は含まれてない。それはSiteVisitorデータのラベルになっている。

5.2 Evaluation settings

AdClickerとSiteVisitorデータセットはマルチラベル。
あるユーザーは複数の広告をクリックするし、様々な広告主のサイトに訪れるから。
（なので、予測するのは「どの広告をクリックするか」と「どの広告主のサイトに来訪するか」かな）

このマルチラベルタスクを、二値分類タスクに変換している。（広告キャンペーン5つそれぞれの二値分類と、広告主5つそれぞれの二値分類）

二値分類タスクにはロジスティックリグレッションを用いている。評価はAUC。

5.3 Proposed methods and baselines

試した手法は大きく4つに分けられる

  • ベースライン
  • ベクトルモデル（word2vec, PV-DM）
  • PV-DM系 ＋ URLベクトルの単純平均（both）
  • PV-DM ＋ skipgram

ベースライン

Bin : ユーザーの各ページごとに来訪したかどうか
Freq : ユーザーの各ページごとの来訪回数

ベクトルモデル

word2vec系とPV-DM系

クリック、ページ来訪の予測に用いる特徴量は、それぞれ下記

  • word2vec: ユーザー表現にURLベクトルの単純平均
  • PV-DM: ユーザー表現にユーザーベクトル

PV-DM ＋ URLベクトルの単純平均

PV-DM系の一部に、

  • ユーザーベクトル
  • URLベクトルの単純平均
    を結合したものを特徴量としている。（bothとついてるもの）

PV-DM + skipgram

PV-DMとskipgramを結合したものを特徴量とする

5.4 Results

image.png

図の見方

  • 太字：ベストパフォーマンス
  • 下線：word2vecとPV-DMのもののみでのベスト（both等は含まない）

気づき

  • データセットの違いによって良い手法は異なった
  • URLをそのまま使う（Bin, Freq）のはよくない
  • Backward PV-DMがPV-DM, Reverse PV-DMと比べてよかった。違いはcontext windowのスライドする方向だけ（言い換えるとSGDの入力の順番）
    • セッションの後ろの方にユーザーの興味の情報があるため
  • bothの方がよかった。

6. Related Work

  • HCRFモデル
  • RNN
  • LSTM

7. Conclusion and Future Work

Backward PV-DMについて提案した。
今後の研究は3つの方向性がありそうだ。

  1. 検索クエリやサイトコンテンツを用いること（URLだけだとsimleでスケーラビリティがあるのが良い）
  2. ユーザー表現を得るための手法として、半教師、マルチラベル、マルチタスクを調査したい
  3. LSTM,RNNに興味がある
0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?