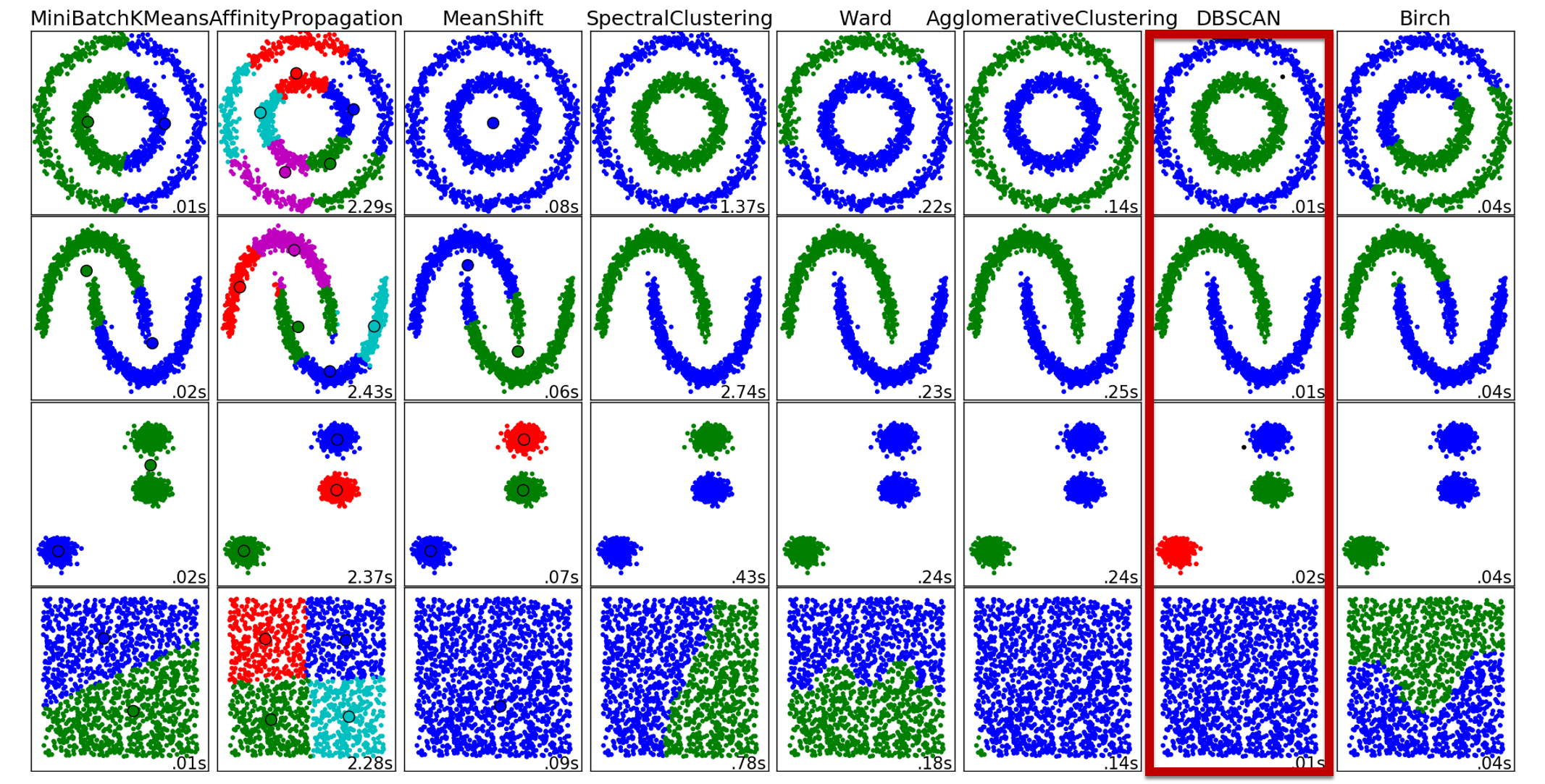
DBSCANは"密度ベース"のクラスタリング手法である。
DBSCANが提案された論文は
Martin Ester,Hans-Peter Kriegel,Jorg Sander,Xiaowei Xu. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. Proccrdings of 2ndInternational Conference on Knowledge Discovery and Data Mining (KDD-96),1996.
で、scikit-learnにもこの論文のアルゴリズムが提案されている。
DBSCANのアルゴリズムはWikiには以下のように記載されている。
DBSCAN requires two parameters: ε (eps) and the minimum number of points required to form a dense region[a] (minPts). It starts with an arbitrary starting point that has not been visited. This point's ε-neighborhood is retrieved, and if it contains sufficiently many points........ (http://en.wikipedia.org/wiki/DBSCAN)
これを私なりに解釈してみる。
半径εの中に点がいくつあるかでその領域をクラスタとして判断している.さらに近傍の密度がある閾値を超えている限り,クラスタを成長させ続けることができるので,近傍付近全体を領域としてみなすことができる
図にしてみるとこんな感じ。
この動画を見ればDBSCANの事がよーーく分かる(と思います)。
http://www.youtube.com/watch?v=5E097ZLE9Sg
メリット
①Mean-shiftとは違い、クラスタ数を設定しなくてもよい
②クラスタが再帰的に計算されるので、outlierに対して頑健である。
デメリット
①計算コストが高く、リアルタイム性のアプリケーションには実装しにくい
最後にソースコードを記載する。
epsで探索する範囲(ある点Xから点がいくつあるか)、min_samplesでepsの中にいくつ点が存在していたらクラスタだとみなすかを決める。
def (eps,min_samples):
db = DBSCAN(eps, min_samples).fit(point_data)
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
print('Estimated number of clusters: %d' % n_clusters_)