はじめに
確率論や統計学の勉強をしていると
\int_{a}^{b}{x\hspace{1pt}dF(x)}
みたいな形の積分に遭遇することがあります。初見では「$dx$なら分かるけど$dF(x)$ってなんやねん???」となると思います。この積分はスティルチェス積分と呼ばれているやつなのですが、確率や統計の勉強中に出くわしたときに詰まないように、この記事では大まかなところをまとめておくことにします。
この記事の結論
$X$を累積分布関数$F(x)$を持つ確率変数とします。このとき、$h(X)$の期待値$\mathbb{E}[h(X)]$はスティルチェス積分を用いて以下のように書けます。
\mathbb{E}[h(X)]=\int_{-\infty}^{\infty}{h(x)dF(x)}= \left\{
\begin{array}{ll}
\sum_{i=1}^{\infty}h(x_i)\mathbb{P}(x_i) & (Xが離散型,\mathbb{P}は確率関数) \\
\int_{-\infty}^{\infty}{h(x)f(x)dx} & (Xが連続型,fは確率密度関数) \\
\end{array}
\right.
スティルチェス積分を使うと離散型と連続型の確率変数の期待値を統一的に表現できて嬉しいです。
この記事で重要な部分はここまで終わりです。これ以降はスティルチェス積分を定義して、なぜ上記の式が成り立つのかを見ていきます。また、本記事では緑色の背景と黄色の背景を以下のように使い分けています。
緑色の背景の部分では定義を記載します。
黄色の背景の部分では定理を記載します。
前提知識
この記事でスティルチェス積分について考えるときに出てくる前提知識をこの項にまとめておきます。
有界性
まずは有界の定義を紹介します。イメージとしては値がある限られた範囲内にあり、無限大になったりしないような状態のことです。
有界集合
実数全体の集合$\mathbb{R}$の部分集合$A$が有界であるとは、任意の$a\in A$に対して、$$|a|\leq M$$を満たすような$M> 0$が存在することである。
ここで関数$f: I\rightarrow\mathbb{R}$を考えると、値域$f(x)$は$\mathbb{R}$の部分集合なので、関数$f$に対しても有界性を同様に定義することが出来ます。
有界関数
集合$I$上で定義された関数$f:I\rightarrow\mathbb{R}$に対して、ある$M>0$が存在して、
|f(x)|\leq M
が成立するとき、関数$f$は有界であるという。
関数の連続性
関数が連続であるとは、関数が途切れずつながっている状態のことです。それをきちんとした言葉で書いてあげると以下のようになります。
連続
関数$f(x)$が$x=c$で連続であるとは、任意の$\epsilon > 0$に対して、ある$\delta=\delta(\epsilon,c)>0$が存在して、
|x-c|<\delta\Rightarrow|f(x)-f(c)|<\epsilon
が成立することである。また、すべての$c\in[a, b]$で$f(x)$が連続であるとき、関数$f(x)$は区間$[a, b]$で連続であるという。
要は「$x$を$c$にどんどん近づけていったときに$f(x)$も$f(c)$に近づいていけば連続」ということを言っています。これに対して、より強いことを主張している一様連続という概念があります。連続の定義における$\delta=\delta(\epsilon,c)$は$\epsilon$と$c$に依存しています。したがって、ある一点$x=c_1$において$\delta_1=\delta(\epsilon,c_1)$をとったときに連続の定義式が成立していたとしても、別の点$x=c_2$では同じ$\delta_1$で連続の定義式が成立しているかどうかは定かではありません。そこでこれを保証しようというのが一様連続の考え方です。
一様連続
関数$f(x)$が区間$[a, b]$で一様連続であるとは、任意の$\epsilon > 0$に対して、ある$\delta=\delta(\epsilon)>0$が存在して、任意の$x, c\in[a, b]$に対して、
|x-c|<\delta\Rightarrow|f(x)-f(c)|<\epsilon
が成立することである。
一様連続における$\delta=\delta(\epsilon)$は$\epsilon$だけに依存していて、場所によらない共通の$\delta$で連続が定義されていることがポイントです。この定義から一様連続であれば連続であることが分かります。加えて以下の定理が成立します。
連続と一様連続の関係
有界閉区間$[a, b]$上で連続な関数は$[a, b]$上で一様連続である。
スティルチェス積分の性質を証明するときにちょっとだけこの定理を使います。
平均値の定理
平均値の定理
関数$f(x)$が区間$[a, b]$で微分可能であるとする。このとき、
f'(c)=\frac{f(b)-f(a)}{b-a}
を満たす$c\in(a,b)$が存在する。
点$(a,f(a))$と点$(b,f(b))$を結んだ直線に対して、それに平行な接線を引ける点$c$が$a$と$b$の間に存在することを言っています。この定理もあとでちょっとだけ使用します。
単調性
単調増加
関数$f: D\rightarrow R$が単調増加であるとは、$x_1<x_2$を満たす$x_1,x_2\in D$に対して、$f(x_1)\leq f(x_2)$が成立することである。
$x$の値が大きくなったとき$f(x)$の値が「変わらない or 大きくなる」ということを言っています。変わらないことを許容しているので本当は「単調非減少」という言い方が正確です。確率論に関連する関数では累積分布関数は一般に単調増加関数になっています。
リーマン積分
高校数学でもやるようないわゆる普通の積分はリーマン積分と呼ばれています。スティルチェス積分はこのリーマン積分の一般化となっているので、まずはリーマン積分の定義を確認しておきます。
リーマン積分の定義
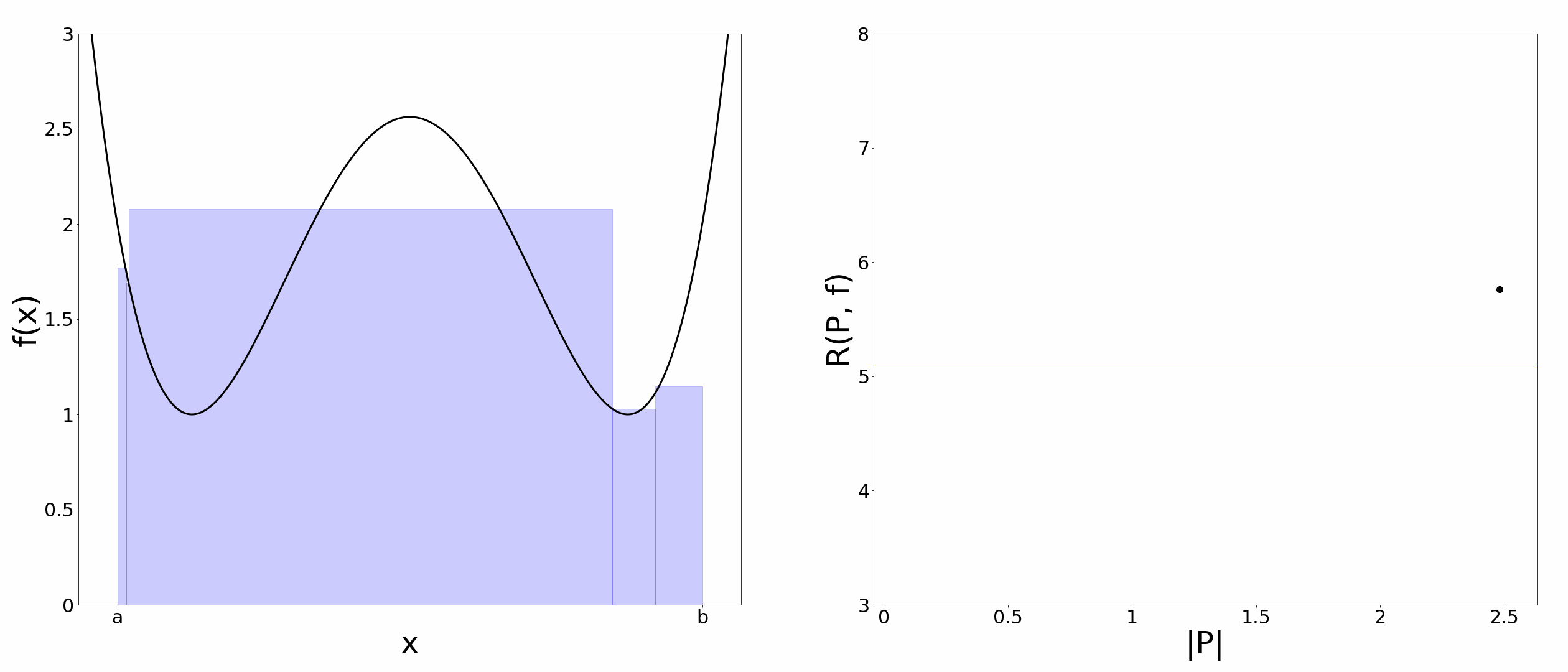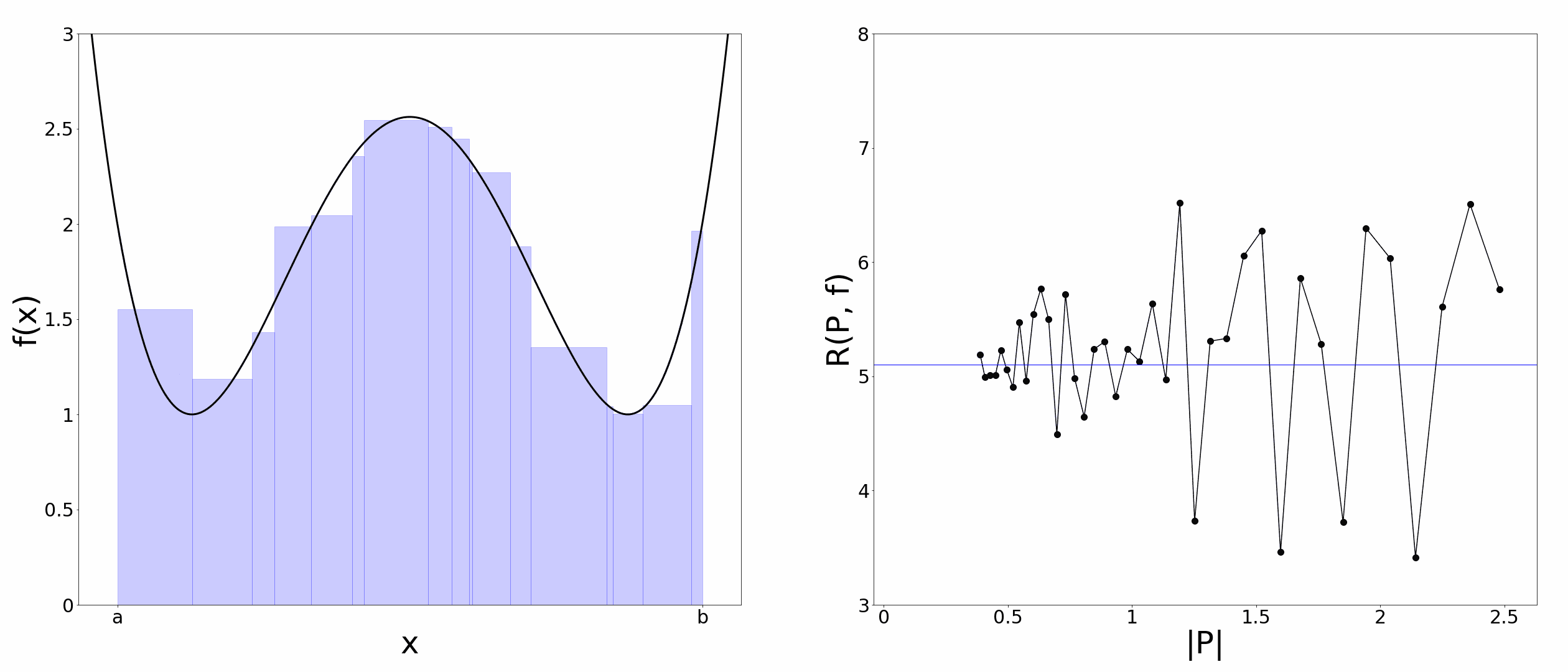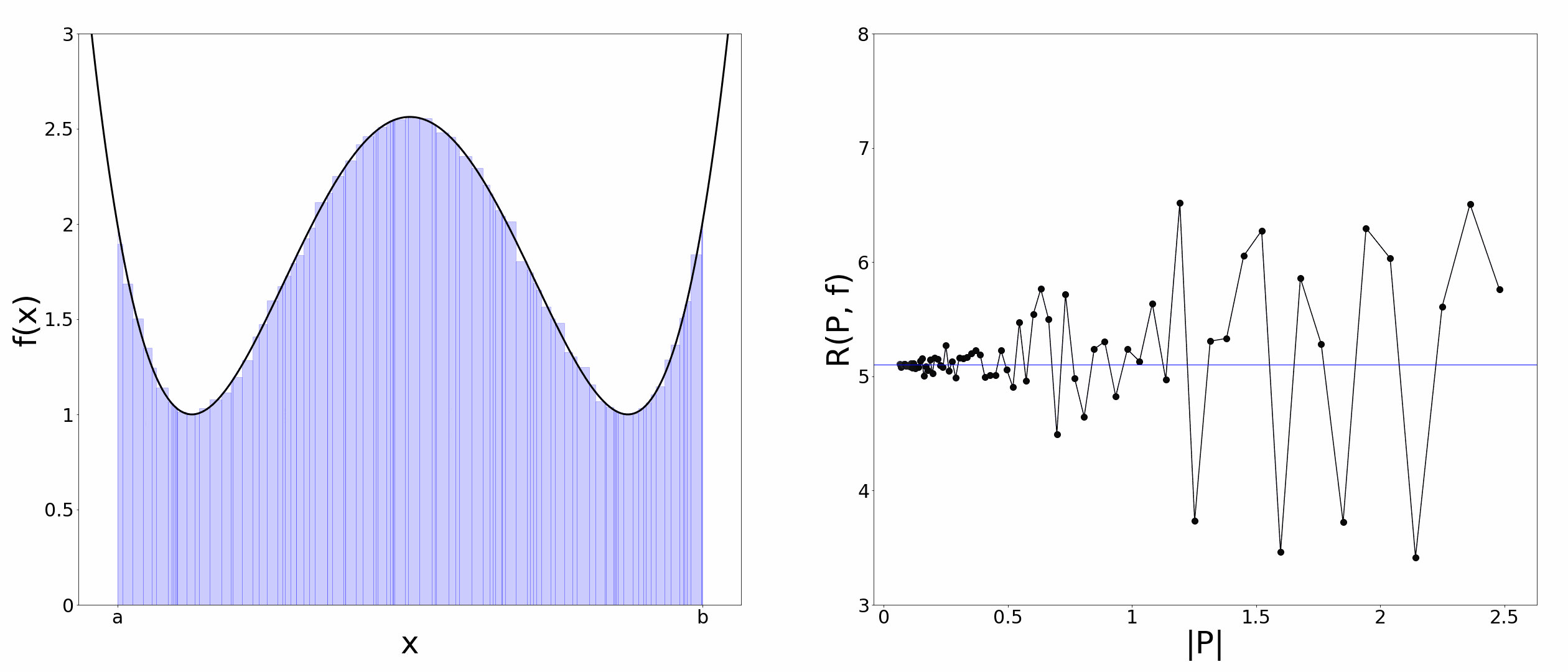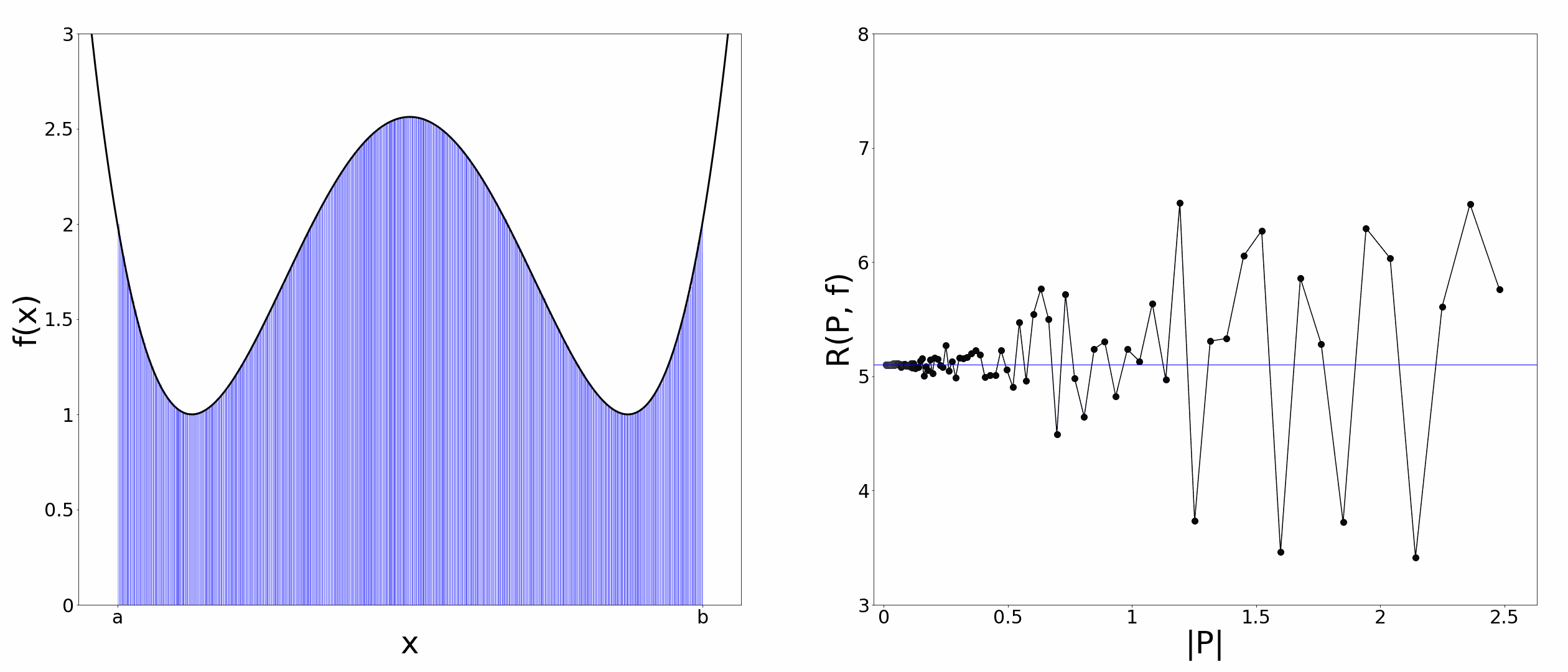
$f(x)$を区間$[a,b]$上で定義された有界な関数とします。そして区間$[a,b]$を$a=x_0<x_1<x_2\cdots<x_{n-1}<x_n=b$のように小区間に分割し、分割点の集合$P=\lbrace x_0,x_1,\ldots,x_n\rbrace$を$[a,b]$の分割と呼ぶことにします。また、小区間の幅の最大値を$|P|=\max(x_1-x_0, \ldots,x_n-x_{n-1})$とします。ここで、$t_i\in[x_{i-1}, x_i] \hspace{5pt} (i=1,2,\ldots,n)$のように各小区間内に代表点$t_i$をとり、以下のような量を考えます。
R(P,f)=\sum_{i=1}^{n}{f(t_i)(x_i-x_{i-1})}
この$R(P,f)$を$f(x)$のリーマン和と呼びます。リーマン和は各小区間が作る長方形の面積の総和になっているので、以下のアニメーションのように$|P|$を$0$に近づけていくと$R(P,f)$は区間$[a,b]$での$f(x)$の曲線下面積に一致しそうです。そこで、$|P|\rightarrow0$における$R(P,f)$の極限値をリーマン積分の定義にしてしまいましょう。
リーマン積分の定義①
$|P|\rightarrow0$の極限を考えたとき、$R(P,f)$が$P, \lbrace t_i \rbrace$の取り方によらず一定の値に収束するならば、$f(x)$は区間$[a,b]$上でリーマン積分可能であるという。この極限値を区間$[a,b]$での$f(x)$のリーマン積分と呼んで、
\lim_{|P| \to 0}R(P,f)=\int_{a}^{b}{f(x)dx}
と表記する。
このリーマン積分の定義を$\epsilon-\delta$論法を使ってもう少し正確に表現すると以下のようになります。
リーマン積分の定義②
任意の$\epsilon > 0$に対して、ある$\delta=\delta(\epsilon)>0$が存在して、$0<|P|<\delta$を満たす区間$[a,b]$の任意の分割$P$と$P$の任意の代表点$\lbrace t_i\rbrace$に対して、
|R(P,f)-A|<\epsilon
が成立するとき、$f(x)$は区間$[a,b]$上でリーマン積分可能であるという。この$A$を区間$[a,b]$での$f(x)$のリーマン積分と呼んで、
A=\int_{a}^{b}{f(x)dx}
と表記する。
今回の記事ではこちらの$\epsilon-\delta$論法による積分の定義をメインに話を進めていきます。
リーマン-スティルチェス積分
この記事で紹介するスティルチェス積分はリーマン積分の一般化となっており、リーマン-スティルチェス積分と呼ばれています。とはいえ、リーマン-スティルチェス積分はリーマン積分とほとんど同じように定義することが出来ます。そして、確率や統計の分野で使われる理由になっている良い性質を持っています。
リーマン-スティルチェス積分の定義
$f(x)$を区間$[a,b]$上で定義された有界な関数、$g(x)$を区間$[a,b]$上で単調増加な関数とします。また、$P=\lbrace x_0,x_1,\ldots,x_n\rbrace$を$[a,b]$の分割、各小区間内の代表点を$\lbrace t_i \rbrace$とします。これらを用いてリーマン和と似た以下のような量を考えることにします。
R(P,f,g)=\sum_{i=1}^{n}{f(t_i)\lbrace g(x_i)-g(x_{i-1})\rbrace}
これをリーマン-スティルチェス和と呼ぶことにします。通常のリーマン積分では、
\lim_{|P| \to 0}R(P,f)=\lim_{|P| \to 0}\sum_{i=1}^{n}{f(t_i)(x_i-x_{i-1})}=\int_{a}^{b}{f(x)dx}
のように定積分を表記していたので、もし$R(P,f,g)$が$|P|\rightarrow0$の極限で$P,\lbrace t_i \rbrace$の取り方によらずに一定の値に収束するとすれば、
\lim_{|P| \to 0}R(P,f,g)=\lim_{|P| \to 0}\sum_{i=1}^{n}{f(t_i)\lbrace g(x_i)-g(x_{i-1})\rbrace}=\int_{a}^{b}{f(x)dg(x)}
のような表記が自然な気がしてきます。そこで、以下のようにリーマン-スティルチェス積分を定義することにします。
リーマン-スティルチェス積分
任意の$\epsilon > 0$に対して、ある$\delta=\delta(\epsilon)>0$が存在して、$0<|P|<\delta$を満たす区間$[a,b]$の任意の分割$P$と$P$の任意の代表点$\lbrace t_i\rbrace$に対して、
|R(P,f,g)-A|<\epsilon
が成立するとき、$f(x)$は区間$[a,b]$上で$g(x)$に関してリーマン-スティルチェス積分可能であるという。この$A$を区間$[a,b]$での$f(x)$の$g(x)$に関するリーマン-スティルチェス積分と呼んで、
A=\int_{a}^{b}{f(x)dg(x)}
と表記する。
これを見るとリーマン-スティルチェス積分は$g(x)$が出てくる以外は普通のリーマン積分と同じ定義になっています。もし、$g(x)=x$であれば、
\int_{a}^{b}{f(x)dg(x)}=\int_{a}^{b}{f(x)dx}
となるので、リーマン-スティルチェス積分はリーマン積分の一般化であることが分かります。
リーマン-スティルチェス積分の性質①
一つ目の性質として、$g(x)$が積分範囲$[a,b]$で連続な導関数$g'(x)$を持つ場合を考えます。このとき、リーマン-スティルチェス積分を普通のリーマン積分で書くことが出来ます。
リーマン-スティルチェス積分の性質①
$f(x)$が$g(x)$に関して区間$[a,b]$上でリーマン-スティルチェス積分可能であり、$g(x)$は$[a,b]$上で連続な導関数$g'(x)$を持つとする。このとき、
\int_{a}^{b}{f(x)dg(x)}=\int_{a}^{b}{f(x)g'(x)dx}\hspace{10pt}\cdots\hspace{10pt}(2)
が成立する。
(証明)
$(2)$式の左辺に対応するリーマン-スティルチェス和を
R(P,f,g)=\sum_{i=1}^{n}{f(t_i)\lbrace g(x_i)-g(x_{i-1})\rbrace}\hspace{10pt}\cdots\hspace{10pt}(3)
とします。また、$(2)$式の右辺に対応するリーマン和を$h(x)=f(x)g'(x)$と置いて、
R(P,h)=\sum_{i=1}^{n}{h(t_i)(x_i-x_{i-1})}\hspace{10pt}\cdots\hspace{10pt}(4)
とします。平均値の定理より、
g(x_i)-g(x_{i-1})=g'(z_i)(x_i-x_{i-1})
を満たす$z_i\in(x_{i-1},x_i)$が存在するので、リーマン-スティルチェス和は
R(P,f,g)=\sum_{i=1}^{n}{f(t_i)\lbrace g(x_i)-g(x_{i-1})\rbrace}=\sum_{i=1}^{n}{f(t_i)g'(z_i)(x_i-x_{i-1})}
のように書き換えることができます。したがって、$(3)$式と$(4)$式の差は
R(P,f,g)-R(P,h)=\sum_{i=1}^{n}f(t_i)\lbrace g'(z_i)-g'(t_i) \rbrace (x_i-x_{i-1})\hspace{10pt}\cdots\hspace{10pt}(5)
のようになります。いま、$f(x)$は$[a,b]$上で有界な関数なので$|f(x)|\leq M$を満たす$M>0$が存在しています。さらに、連続と一様連続の関係より$g'(x)$は$[a,b]$上で一様連続なので、任意の$\epsilon > 0$に対して、
|z_i-t_i|<\delta_1\Rightarrow |g'(z_i)-g'(t_i)|< \frac{\epsilon}{2M(b-a)}
を満たすような$\delta_1>0$をとることができます。これを$(5)$式に適用すると、$|P|<\delta_1$を満たす分割$P$に対して、
\displaylines{
|R(P,f,g)-R(P,h)|=\lvert\sum_{i=1}^{n}f(t_i)\lbrace g'(z_i)-g'(t_i) \rbrace (x_i-x_{i-1})\rvert \\
\hspace{83pt}<\hspace{5pt}\rvert\sum_{i=1}^{n}M\cdot\frac{\epsilon}{2M(b-a)}\cdot(x_i-x_{i-1})\rvert \\
\hspace{45pt}=\frac{\epsilon}{2(b-a)}\rvert\sum_{i=1}^{n}(x_i-x_{i-1})\rvert \\
\hspace{13pt}=\frac{\epsilon}{2(b-a)}\rvert (b-a)\rvert \\
=\frac{\epsilon}{2}\hspace{5pt}\hspace{10pt}\cdots\hspace{10pt}(6)
}
のような不等式が成立します。一方で、$f(x)$は$[a,b]$上で$g(x)$に関してリーマン-スティルチェス積分可能なので、任意の$\epsilon > 0$に対して、$|P|<\delta_2$を満たす区間$[a,b]$の任意の分割$P$と$P$の任意の代表点$\lbrace t_i\rbrace$を考えると、
|R(P,f,g)-\int_{a}^{b}{f(x)dg(x)}|<\frac{\epsilon}{2}\hspace{10pt}\cdots\hspace{10pt}(7)
を満たすような$\delta_2>0$をとることができます。したがって、任意の$\epsilon > 0$に対して、$\delta=\min(\delta_1,\delta_2)$と置くと、$(6)$式と$(7)$式から、$|P|<\delta$を満たす分割$P$に対して、
|R(P,f,g)-\int_{a}^{b}{f(x)dg(x)}|+|R(P,f,g)-R(P,h)|<\epsilon
が成立します。これに三角不等式1を適用すると、
|R(P,h)-\int_{a}^{b}{f(x)dg(x)}|<\epsilon\hspace{10pt}\cdots\hspace{10pt}(8)
となります。よって、$(8)$式とリーマン積分の定義から
\int_{a}^{b}{f(x)g'(x)dx}=\int_{a}^{b}{f(x)dg(x)}
が得られます。$□$
リーマン-スティルチェス積分の性質②
$g(x)$が積分範囲$[a,b]$上で連続な導関数を持たない場合はどのようにスティルチェス積分を計算すればよいでしょうか?その例として以下のような値がジャンプする点のある関数について考えてみます。

リーマン-スティルチェス積分の性質②
$g(x)$を区間$[a,b]$上で定義された以下のような関数とする。
\displaylines{
g(x) = \left\{
\begin{array}{ll}
\lambda_1 & (a\leq x<b) \\
\lambda_2 & (x=b)
\end{array}
\right.
}
また、$f(x)$を区間$[a,b]$上で定義された有界な関数で$x=b$で連続であるとする。このとき、
\int_{a}^{b}{f(x)dg(x)}=(\lambda_2-\lambda_1)f(b) \hspace{10pt}\cdots\hspace{10pt}(9)
が成立する。
(証明)
区間$[a,b]$は$a=x_0<x_1<x_2\cdots<x_{n-1}<x_n=b$のように分割されているので、$i=1,\ldots,n$に対して、$g(x_i)-g(x_{i-1})$の値を考えると、$i=n$の時に$g(x_n)-g(x_{n-1})=\lambda_2-\lambda_1$となり、$i\neq n$では$g(x_i)-g(x_{i-1})=\lambda_1-\lambda_1=0$となります。よって、$(9)$式の左辺に対応するリーマン-スティルチェス和を考えると
R(P,f,g)=\sum_{i=1}^{n}{f(t_i)\lbrace g(x_i)-g(x_{i-1})\rbrace}=(\lambda_2-\lambda_1)f(t_n)
となることが分かります。したがって、
|R(P,f,g)-(\lambda_2-\lambda_1)f(b)|=|\lambda_2-\lambda_1||f(t_n)-f(b)|\hspace{10pt}\cdots\hspace{10pt}(10)
が成立します。いま、$f(x)$は$x=b$で連続なので、任意の$\epsilon > 0$に対して、
|t_n-b|<\delta\Rightarrow|f(t_n)-f(b)|<\frac{\epsilon}{|\lambda_2-\lambda_1|}
を満たすような$\delta>0$をとることができます。これを$(10)$式に適用すると、$|P|<\delta$を満たす分割$P$に対して、
\displaylines{
|R(P,f,g)-(\lambda_2-\lambda_1)f(b)|=|\lambda_2-\lambda_1||f(t_n)-f(b)| \\
\hspace{115pt}<|\lambda_2-\lambda_1|\cdot\frac{\epsilon}{|\lambda_2-\lambda_1|} \\
\hspace{33pt}=\epsilon
}
のような不等式が成立します。よって、リーマン-スティルチェス積分の定義から、
\int_{a}^{b}{f(x)dg(x)}=(\lambda_2-\lambda_1)f(b)
が得られます。$□$
リーマン-スティルチェス積分の性質③
続いて$g(x)=g_1(x)+g_2(x)$のように$g(x)$が関数の和として書ける場合の性質を紹介します。
リーマン-スティルチェス積分の性質③
$f(x)$が区間$[a,b]$上で$g_1(x)$および$g_2(x)$についてリーマン-スティルチェス積分可能であるとする。このとき、$f(x)$は$g(x)=g_1(x)+g_2(x)$についてリーマン-スティルチェス積分可能であり、
\int_{a}^{b}{f(x)dg(x)}=\int_{a}^{b}{f(x)dg_1(x)}+\int_{a}^{b}{f(x)dg_2(x)}
が成立する。
(証明)
\int_{a}^{b}{f(x)dg_1(x)}=A,\hspace{15pt}\int_{a}^{b}{f(x)dg_2(x)}=B
と置きます。$f(x)$は区間$[a,b]$上で$g_1(x)$についてリーマン-スティルチェス積分可能なので、任意の$\epsilon > 0$に対して、$|P|<\delta_1$を満たす区間$[a,b]$の任意の分割$P$と$P$の任意の代表点$\lbrace t_i\rbrace$を考えると、
|R(P,f,g_1)-A|<\frac{\epsilon}{2}
を満たすような$\delta_1>0$をとることができます。$g_2(x)$についても同様に
|R(P,f,g_2)-B|<\frac{\epsilon}{2}
を満たすような$\delta_2>0$をとることができます。そこで、任意の$\epsilon > 0$に対して、$\delta=\min(\delta_1,\delta_2)$と置くと、$|P|<\delta$を満たす分割$P$に対して、
|R(P,f,g_1)-A|+|R(P,f,g_2)-B|<\epsilon
が成立します。この不等式に三角不等式を適用して整理すると、
\displaylines{
|R(P,f,g_1)-A+R(P,f,g_2)-B|\hspace{146pt}\\
=|R(P,f,g_1)+R(P,f,g_2)-(A+B)| \hspace{148pt}\\
=|\sum_{i=1}^{n}{f(t_i)\lbrace g_1(x_i)-g_1(x_{i-1})\rbrace}+\sum_{i=1}^{n}{f(t_i)\lbrace g_2(x_i)-g_2(x_{i-1})\rbrace}-(A+B)| \\
=|\sum_{i=1}^{n}{f(t_i)[ g_1(x_i)+g_2(x_i)-\lbrace g_1(x_{i-1})+g_2(x_{i-1})\rbrace}]-(A+B)| \hspace{38pt}\\
=|R(P,f,g_1+g_2)-(A+B)|\hspace{180pt} \\
=|R(P,f,g)-(A+B)|<\epsilon\hspace{187pt}
}
となるので、リーマン-スティルチェス積分の定義より、
\int_{a}^{b}{f(x)dg(x)}=\int_{a}^{b}{f(x)dg_1(x)}+\int_{a}^{b}{f(x)dg_2(x)}
が得られます。$□$
リーマン-スティルチェス積分の性質④
通常のリーマン積分と同様の性質なので証明は省略しますが、リーマン-スティルチェス積分においても積分する範囲を分割できます。
リーマン-スティルチェス積分の性質④
$a<c<b$に対して、
\int_{a}^{b}{f(x)dg(x)}=\int_{a}^{c}{f(x)dg(x)}+\int_{c}^{b}{f(x)dg(x)}
が成立する。
スティルチェス積分で期待値を表してみる
それではここまで紹介してきたスティルチェス積分の性質を使って、確率変数の期待値がどのように表現されるかを見てみます。
連続型確率変数の場合
$X$を累積分布関数$F(x)$を持つ連続型確率変数とします。$X$が連続型確率変数であれば確率密度関数$f(x)$が存在して、
f(x)=F'(x)
のように確率密度関数は累積分布関数の微分で求めることができます。累積分布関数$F(x)$は単調増加関数なので、$F(x)$に関するリーマン-スティルチェス積分
\int_{-\infty}^{\infty}{xdF(x)}
を定義することができて2、これにリーマン-スティルチェス積分の性質①を適用すると、
\int_{-\infty}^{\infty}{xdF(x)}=\int_{-\infty}^{\infty}{xF'(x)dx}=\int_{-\infty}^{\infty}{xf(x)dx}=\mathbb{E}[X]
となり、連続型確率変数$X$の期待値がリーマン-スティルチェス積分で表現できることが分かります。
離散型確率変数の場合
$X$を累積分布関数$F(x)$を持つ離散型確率変数とします。$X$が離散型の場合は通常の意味での確率密度関数が存在しません。そこでリーマン-スティルチェス積分
\int_{-\infty}^{\infty}{xdF(x)} \hspace{10pt}\cdots\hspace{10pt}(11)
を計算するためにリーマン-スティルチェス積分の性質②を適用することを考えます。まず、$X$の確率関数を$\mathbb{P}(x)$、$X$の取りうる値を$k_1,\ldots,k_n$とします。すると累積分布関数$F(x)$は以下のように$k_1,\ldots,k_n$でジャンプするような階段状の関数となります。
\displaylines{
F(x) = \left\{
\begin{array}{ll}
0 & (-\infty<x<k_1) \\
\mathbb{P}(k_1) & (k_1\leq x<k_2) \\
\mathbb{P}(k_1)+\mathbb{P}(k_2) & (k_2\leq x<k_3) \\
\vdots \\
\mathbb{P}(k_1)+\cdots+\mathbb{P}(k_{n-2}) & (k_{n-2}\leq x<k_{n-1}) \\
\mathbb{P}(k_1)+\cdots+\mathbb{P}(k_{n-1}) & (k_{n-1}\leq x<k_{n}) \\
1 & (k_{n}\leq x<\infty) \\
\end{array}
\right.
}
そして、リーマン-スティルチェス積分の性質④を使って$(11)$式の積分範囲をを$k_1,\ldots,k_n$ごとに分割すると、
\int_{-\infty}^{\infty}{xdF(x)}=\int_{-\infty}^{k_1}{xdF(x)}+\int_{k_1}^{k_2}{xdF(x)}+\cdots+\int_{k_{n-1}}^{k_n}{xdF(x)}
のように書くことが出来るので、各項にリーマン-スティルチェス積分の性質②を適用すれば、
\int_{-\infty}^{\infty}{xdF(x)}=\sum_{i=1}^{n}k_i\mathbb{P}(k_i)=\mathbb{E}[X]
となり、離散型確率変数$X$の期待値もリーマン-スティルチェス積分で表現できることが分かります。
連続型と離散型が混ざっている場合
例として区間$[0,1]$上で定義される以下のような累積分布関数$F(x)$を持つ確率変数$X$を考えてみます。
\displaylines{
F(x) = \left\{
\begin{array}{ll}
x^2 & (0\leq x < \frac{1}{2}) \\
\lambda_1 & (\frac{1}{2} \leq x<\frac{3}{4}) \\
\lambda_2 & (\frac{3}{4}\leq x<1) \\
1 & (x=1) \\
\end{array}
\right.
}
グラフを書いてみると以下のようになります。

この確率変数$X$は$0\leq x < \frac{1}{2}$の範囲では連続値をとり、$\frac{1}{2} \leq x\leq 1$の範囲では$\mathbb{P}(X=\frac{1}{2})=\lambda_1-\frac{1}{4}$、$\mathbb{P}(X=\frac{3}{4})=\lambda_2-\lambda_1$、$\mathbb{P}(X=1)=1-\lambda_2$のように離散値をとる確率変数になっています。この確率変数$X$の期待値$\mathbb{E}[X]$は、$0\leq x < \frac{1}{2}$の範囲での確率密度関数が$(x^2)'=2x$なので、
\displaylines{
\mathbb{E}[X]
=\int_{0}^{\frac{1}{2}}{2x^2dx}+\frac{1}{2}\cdot\mathbb{P}(X=\frac{1}{2})+\frac{3}{4}\cdot\mathbb{P}(X=\frac{3}{4})+1\cdot\mathbb{P}(X=1)
}
で与えられます。では、この確率変数に対するリーマン-スティルチェス積分$\int{xdF(x)}$はどのような値になるでしょうか?一般に累積分布関数は連続関数と階段型関数の和で表すことが可能です。今回の場合は
\displaylines{
C(x) = \left\{
\begin{array}{ll}
x^2 & (0\leq x < \frac{1}{2}) \\
\frac{1}{4} & (\frac{1}{2} \leq x\leq 1) \\
\end{array}
\right.
\hspace{39pt}
D_1(x) = \left\{
\begin{array}{ll}
0 & (0\leq x < \frac{1}{2}) \\
\lambda_1-\frac{1}{4} & (\frac{1}{2} \leq x\leq 1) \\
\end{array}
\right.
\hspace{1pt}
}
\displaylines{
D_2(x) = \left\{
\begin{array}{ll}
0 & (0\leq x < \frac{3}{4}) \\
\lambda_2-\lambda_1 & (\frac{3}{4} \leq x\leq 1) \\
\end{array}
\right.
\hspace{15pt}
D_3(x) = \left\{
\begin{array}{ll}
0 & (0\leq x < 1) \\
1-\lambda_2 & (x=1) \\
\end{array}
\right.
\hspace{10pt}
}
のような連続関数$C(x)$と階段型関数$D_1(x),D_2(x),D_3(x)$を用いて、
F(x) = C(x)+D_1(x)+D_2(x)+D_3(x)
と書くことが出来ます。ここでリーマン-スティルチェス積分は、リーマン-スティルチェス積分の性質①②③④を用いると、
\displaylines{
\int_{0}^{1}{xdF(x)}=\int_{0}^{1}{xdC(x)}+\int_{0}^{1}{xdD_1(x)}+\int_{0}^{1}{xdD_2(x)}+\int_{0}^{1}{xdD_3(x)} \\
\hspace{62pt}=\int_{0}^{\frac{1}{2}}{xC'(x)dx}+\frac{1}{2}\cdot(\lambda_1-\frac{1}{4})+\frac{3}{4}\cdot(\lambda_2-\lambda_1)+1\cdot(1-\lambda_2)\\
\hspace{62pt}=\int_{0}^{\frac{1}{2}}{2x^2dx}+\frac{1}{2}\cdot\mathbb{P}(X=\frac{1}{2})+\frac{3}{4}\cdot\mathbb{P}(X=\frac{3}{4})+1\cdot\mathbb{P}(X=1)\\
=\mathbb{E}[X]\hspace{175pt}
}
であることが分かります。このように、連続型と離散型が混ざっているような確率変数$X$の期待値もリーマン-スティルチェス積分で表現できることが分かります。
まとめると...
結局のところ、スティルチェス積分を用いることで離散型だろうが連続型だろうが確率変数$X$の期待値$\mathbb{E}[X]$を
\mathbb{E}[X]=\int_{-\infty}^{\infty}{xdF(x)}
のように表現できます。より一般的には、確率変数$X$に対して$h(X)$の期待値$\mathbb{E}[h(X)]$が
\mathbb{E}[h(X)]=\int_{-\infty}^{\infty}{h(x)dF(x)}
となるので、例えば$X$のモーメント母関数$M_X(t)$であれば
M_X(t)=\mathbb{E}[e^{tX}]=\int_{-\infty}^{\infty}{e^{tx}dF(x)}
のように書くことが出来ます。スティルチェス積分を使うことで色々な確率変数について統一的に議論することが出来て便利ですね。
終わりに
応用上は詳細な理論に踏み込まなくても、まずはスティルチェス積分のお気持ちを感じ取れたらOKだと思います。というか別にスティルチェス積分なんて知らなくても良いという説もあります。
参考文献
1.André I. Khuri (2002) Advanced Calculus with Applications in Statistics. 2nd Edition,Wiley Series in Probability and Statistics.
2.https://scholarworks.rit.edu/cgi/viewcontent.cgi?article=3197&context=article
3.http://mathonline.wikidot.com/linearity-of-the-integrator-of-riemann-stieltjes-integrals#toc0