はじめに
今回は一般化加法モデル (GAM)にニューラルネットワークを適用したNeural Additive Modelを紹介しようと思います。
今回参考にしたNeural Additive Modelの原著論文はこちらです↓
この記事で使用したコードは以下のGitHubリポジトリに置いてあります。ニューラルネットワークはPyTorchを用いて構築しています。
一般化加法モデル (GAM)
目的変数$y$と$K$個の特徴量$x_1,\ldots,x_K$のようなデータがあるとき、GAMでは非線形な関数$f$を用いて
g(\mu)=\beta + f_1(x_1) + \cdots + f_K(x_K) \hspace{50pt}(1)
のようなモデルを想定します。なお、$g$はリンク関数、$E[y]=\mu$、$E[f_i]=0$とします。GAMでは特徴量間の加法性を仮定しているため、$f_i(x_i)$の形が分かれば構築したモデルにおいて個々の特徴量が目的変数にどのように影響を与えているかを容易に理解することができます。そのため、GAMは一般化線形モデルよりも高い表現力を持ち、普通のニューラルネットワークのような複雑なモデルよりも解釈性の高いモデルといえます。
では具体的にどのように$f_i(x_i)$を推定するか言うと、よく使われる方法の一つが以下のように$f_i(x_i)$を基底関数$b$の線形結合として表す方法です。
f_{i}(x_i)=\sum_{j=1}^{p}\beta_{ij} b_{ij}(x_i)
特徴量を基底関数で変換した$b_{ij}(x_i)$を新たな特徴量と考えると、結局のところ$(1)$式は一般化線形モデルになるので最尤法で未知パラメータ$\beta_{ij}$を推定することにより、非線形な関数$f_i(x_i)$を推定することができます。
この方法を用いるにはあらかじめ基底関数を選んで特徴量をどのように変換するかを決めておく必要があります。しかし、どんな基底関数が良いのかはデータによって異なるので色々と試行錯誤する必要がありますし、説明変数それぞれに対してベストな基底関数を選ぶ作業はとても面倒です。また、GAMではスプライン基底などの滑らかな関数を表現できる基底関数がよく使われますが、急に値が大きく変動してギザギザしているようなスプラインでは表現しにくいデータも現実には存在します。
このようなGAMの問題点を考えると、例えば以下のような考えが出てくるのは自然です。
どのように特徴量を変換するかもデータから学習してくれればいいのに・・・
よくある基底関数を用いるよりもっと表現力の高い非線形関数を使いたい・・・
「じゃあ非線形関数にニューラルネットワーク使えば良くね?」を実現したのがNeural Additive Modelです。
Neural Additive Models (NAM)
NAMの構造
NAMの考え方は非常にシンプルで、以下のように特徴量ごとにニューラルネットワークを作成して、個々のニューラルネットワークからの出力を足し合わせて最終的な出力とします。

Exp-centered (ExU) hidden units
個々のニューラルネットワークに入力される特徴量が1つだけになると高度にギザギザした関数の学習が難しい場合があるようで、論文では隠れ層の値$h(x)$を通常の方法ではなく以下のように計算することを提案しています。
h(x)=f(e^w * (x-b))
これをExU unitと呼んでいて、$x$が入力された値、$w$と$b$がそれぞれ重みとバイアスパラメータ、$f$は活性化関数です。$e^w$を入力に掛け算することで入力$x$の小さな変化で出力の値を大きく変化させることができるため、ギザギザした関数を学習しやすくなる効果があるようです。活性化関数には値の上限を$1$としたReLUであるReLU-1を使うのが良いみたいです。実際の実装ではExU unitは1層目の隠れ層を計算するときにのみ使われているようでした。
ちなみに自分でNAMを実装すると、ExU unitを使うと学習が上手くいかないことが多かったので、今回の記事ではExU unitは用いていません。(何か間違っているのかな・・・。)
損失関数
NAMの学習では以下の損失関数を最小化するように学習を行っています。
L(\theta) = l(x, y;\theta) + \lambda_1\eta(x;\theta) + \lambda_2 \gamma(\theta)
$l(x, y;\theta)$はタスクに依存する損失関数で、今回の記事の回帰問題では以下のMean Squared Errorを用いています。
l(x, y;\theta)=\frac{1}{N} \sum_{i=1}^{N}(\beta^\theta + \sum_{k=1}^{K}f^\theta_k(x_{ik})-y_i)^2
ここで、$f^\theta_k$は$k$番目の特徴量のニューラルネットワークを表しています。例えば2値分類などでは$l(x, y;\theta)$はcross-entropy lossになったりします。
$\eta(x;\theta)$はoutput penalty、$\gamma(\theta)$は weight decayでそれぞれ
\eta(x;\theta)=\frac{1}{K}\sum_{x}^{}\sum_{k=1}^{K}f^\theta_k(x_{k})
\gamma(\theta)=\sum_{k=1}^{K} \sum_{p}^{} \theta_{kp}^2
のように計算しています。ここで、$\sum_{p}^{} \theta_{kp}^2$は$k$番目の特徴量のニューラルネットワークのすべてのパラメータの2乗和を計算することを意味しています。これらの2つの項は正則化の役割を担っており、正則化の強さを決める$\lambda_1,\lambda_2$は学習のハイパーパラメータになります。
モデルの可視化
NAMを用いる利点はモデルの解釈性が高いことなので、学習が完了した後はモデルがどのように予測を行っているか可視化を行う必要があります。可視化を行う際は、以下のように個々の特徴量に対して対応するニューラルネットワークの最終的な出力をプロットします。

個々の特徴量に対してこのようにプロットを行うとニューラルネットワークの回帰曲線を描くことができるので、特徴量が目的変数にどのような影響を与えているかを一目で確認することができます。
NAMをやってみる
データセット
実際にNAMを用いた回帰分析を実行してみます。今回はカリフォルニア住宅価格のデータセットを用いて、以下のような特徴量から住宅価格を予測するモデルを作成します。

| 変数名 | 変数の内容 |
|---|---|
| MedInc | ブロック内の所得の中央値 |
| HouseAge | ブロック内の築年数の中央値 |
| AveRooms | 1世帯あたりの部屋数の平均値 |
| AveBedrms | 1世帯あたりの寝室数の平均値 |
| Population | ブロック内の人口 |
| AveOccup | 1世帯あたりの世帯人数の平均値 |
| Latitude | 緯度 |
| Longitude | 経度 |
| target | 目的変数:住宅価格 |
普通のニューラルネットワーク
まずは比較対象として普通のニューラルネットワークを用いてモデルを作成し、予測精度を確認します。論文内で用いられていたのと同様に、隠れ層の数が10、各層で100ユニットのニューラルネットワークを用いて学習を行っています。学習結果を以下に示していますが、テストデータの予測値と実測値の相関係数は0.894となりました。

NAM
続いて、NAMの学習を行います。個々のニューラルネットワークの構造は、隠れ層が3層、ユニット数が浅い層からそれぞれ512, 64, 32としています。学習の結果を以下のグラフに示しています。

テストデータの予測値と実測値の相関係数は0.873となり、普通のニューラルネットワークの0.894よりも小さな値になっています。NAMでは個々のニューラルネットワークに入力される特徴量は1つだけなので、普通のニューラルネットワークよりもモデルの表現力は低くなります。したがって、NAMの方が相関係数が小さくなるのは当然の結果でしょう。とはいえ、かなり近い値ではあるので、このデータセットに対してはNAMは普通のニューラルネットワークに匹敵する精度を出せるといってもよさそうです。
続いて、個々のニューラルネットワークの回帰曲線を可視化してみます。
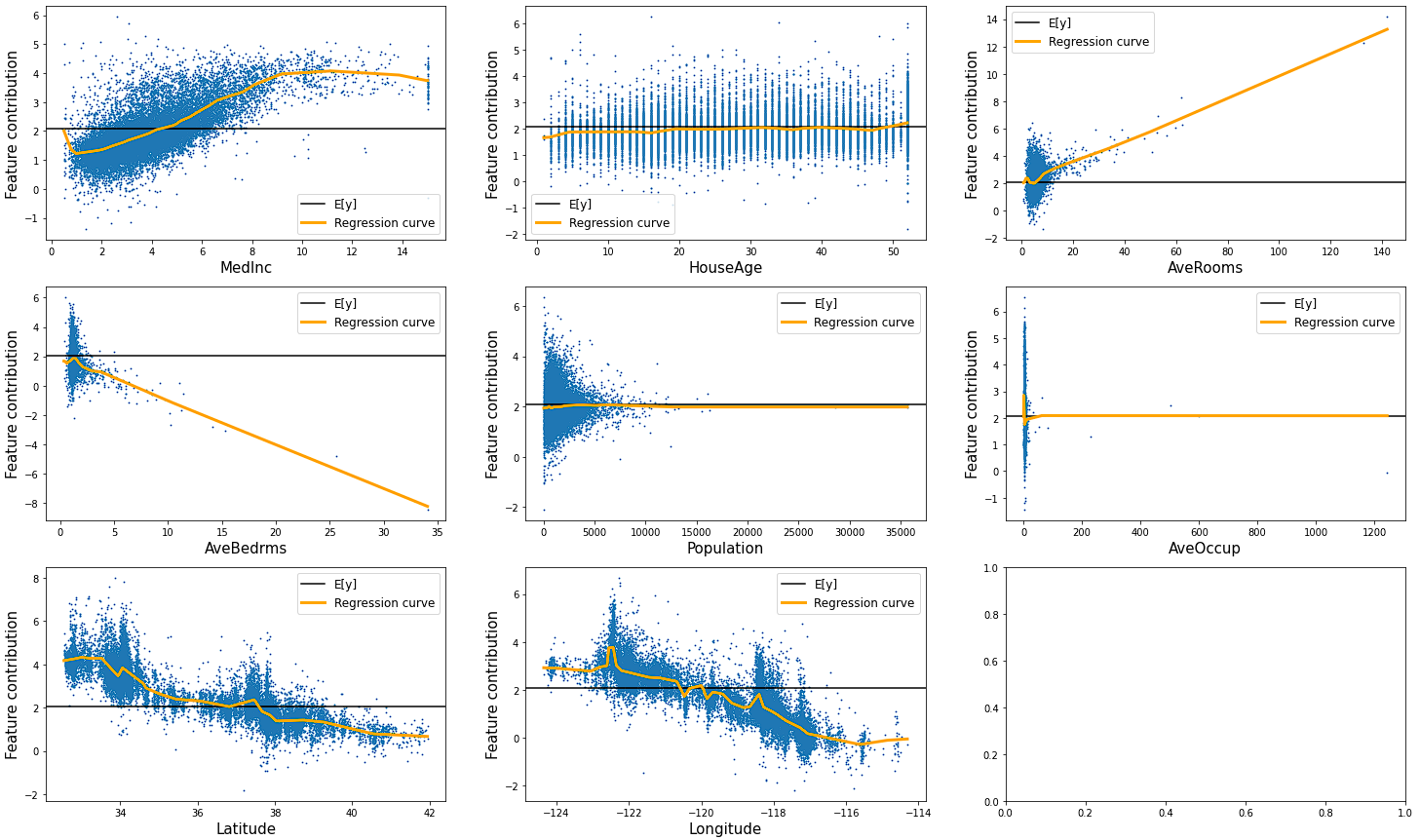
このプロットを確認することで各特徴量が目的変数にどのように影響を与えているかを可視化することができます。このグラフを確認すると例えば以下のような考察ができます。
①MedIncの値が大きくなるほど住宅価格も高くなるが、MedIncがある程度大きくなると住宅価格は頭打ちになる。
②AveRoomsが大きくなると住宅価格も上昇する。
③緯度がプラス方向に大きいほど、経度がマイナス方向に大きいほど住宅価格が上昇する。
④AveBedrmsが大きくなると住宅価格は減少する。
①、②は感覚的にはありそうな気がします。③は場所による住宅価格の相場の知識があれば正しいかどうか判断できそうです。④に関しては部屋数が増えると住宅価格は高くなりそうな気がするので、私の感覚とは逆の傾向になっています。データをもう少し確認してみたくなります。
NAMは予測モデルを作るという目的でももちろん使えると思いますが、このようにデータを理解するという意味でも便利そうです。
NAMに交互作用を追加してみる
NAMは個々の特徴量の効果(主効果)の和で目的変数の値を予測するモデルですが、ここに交互作用を追加するとさらに予測精度が向上しそうな気がします。そこで、参考にした論文からは離れますが、NAMに交互作用を追加するして予測精度がどのように変わるか試してみます。
そこで、以下の図のように先ほど学習したNAMにすべての特徴量を入力とするニューラルネットワーク$f(\boldsymbol{x})$、つまり普通のニューラルネットワークを追加します。学習するときは先ほど学習済みの個々の特徴量のニューラルネットワークのパラメータをすべて固定して、追加した$f(\boldsymbol{x})$のパラメータのみ更新を行います。

上記のように学習を行うと、追加したニューラルネットワーク$f(\boldsymbol{x})$はNAMの個々の特徴量のニューラルネットワーク(主効果)では説明できない部分、つまり交互作用を学習すると考えられます。
実際に学習を行った結果を以下のグラフに示しています。テストデータに対する予測値と実測値の相関係数は0.897となりました。これは普通のニューラルネットワークを用いて学習を行った結果である0.894とほとんど同じ値になっています。普通のニューラルネットワークは最初から特徴量の交互作用を捉えることができるので、NAMに追加したネットワークが交互作用を学習したために似たような値になっていると考えられます。
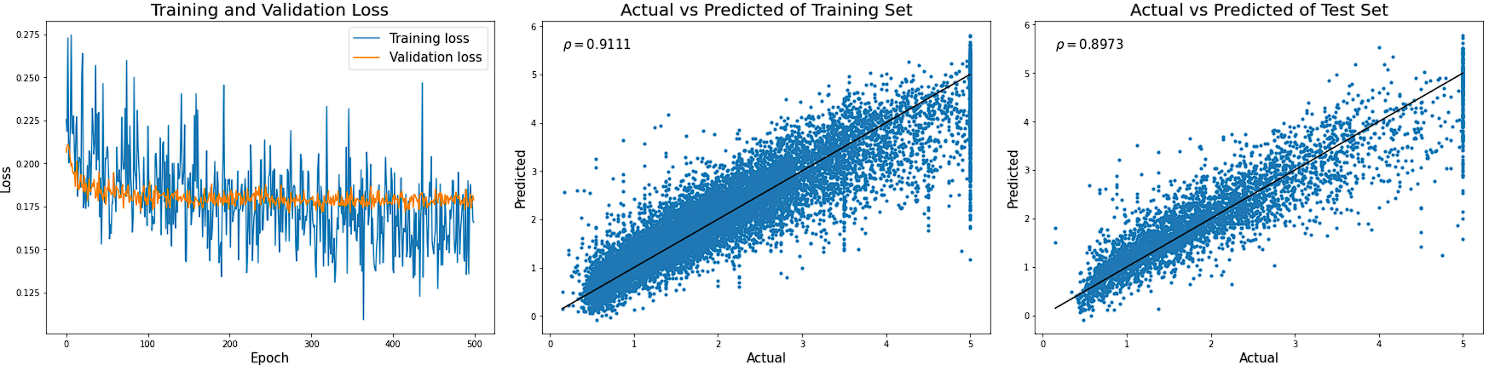
次に、以下のグラフでNAMに交互作用を学習するニューラルネットワーク追加する前後で予測精度の変化を比べてみます。
交互作用を学習するニューラルネットワーク追加することでテストデータに対する予測値と実測値の相関係数が0.873から0.897に増加しています。予測精度は増加していますが、それほど大きな変化ではないので今回用いたデータでは目的変数はほとんど個々の特徴量の効果(主効果のみ)で予測できることになります。逆に交互作用が目的変数の予測に大きな影響を及ぼしていることが分かればNAMよりも複雑なモデルを用いる、どんな交互作用があるのかを調べる、といった方針になるでしょう。このようなNAMを活用したモデリングは予測はもちろん、探索的なデータ分析の目的にも役立つと思います。
終わりに
今回は勉強のためにNAMを自分で実装しましたが、公式の実装がこちらにあります。 また、Microsoftが開発した個々の非線形関数をGradient Boosting Decision Treeで推定するExplainable Boosting Machineもあるので、用途に応じて使い分けできるとよいと思います。Explainable Boosting Machineだと二次交互作用まで網羅的に探索してくれて便利です。
