2018年版 深層学習によるスタイル変換まとめ

スタイル変換とは

まずは例をご覧ください．
コンテンツ画像とスタイル画像を入力すると変換画像が得られます．

このようにコンテンツ画像にスタイル画像の画風を反映することをスタイル変換と言います．
こちらのサイトでは簡単にスタイル変換が試せるので，是非やってみてください．
上記の例はこのサイトで作成した画像です．

論文一覧

深層学習によるスタイル変換の手法を表にまとめました．
大まかな流れとしては

• 学習していないスタイルへ変換できるように
• リアルタイムで変換できるように

研究が進んできています．

手法	概要	変換可能なスタイル数	処理時間(sec)	リンク
Gatys et al.1 CVPR 2016	コンテンツ画像とスタイル画像に近づくよう最適化	$\infty$	500itr 15.862	paper
J. Johnson et al.2 ECCV 2017	1つのスタイル画像でネットワークを訓練	$1$	0.0152	paper github
V. Dumoulin et al.3 ICLR 2017	スタイルごとにInstance Normalizationのパラメータを学習	$N$	0.0114	paper
X. Huang et al.4 ICCV 2017	スタイル画像の平均と分散を使ってInstance Normalization	$\infty$	0.0274	paper github
Y. Li et al.5 NIPS 2017	コンテンツ画像の中間特徴を白色化しスタイル画像のパラメータで変換	$\infty$	0.626	paper github
T. Q. Chen et al.7	コンテンツ画像の中間特徴をスタイル画像の中間特徴で置換	$\infty$	0.0646	paper github
L. Sheng et al.6 CVPR 2018	Liらの手法とChenらの手法の組み合わせ	$\infty$	0.266	paper github

変換可能なスタイル数 $\infty$ は学習していないスタイル画像に対応できることを表します．
処理時間は256pxの画像での結果です．

Image Style Transfer Using Convolutional Neural Networks

Gatys et al. CVPR 2016
CNNを使ってコンテンツ画像とスタイル画像に近くなるようにホワイトノイズを更新します．
モデルは学習済みのVGGを使用し，追加の学習は必要ありません．
スタイル画像を変えることであらゆるスタイルへの変換が可能ですが，
入力のホワイトノイズそのものをbackpropにより更新するため計算コストが高いという欠点があります．

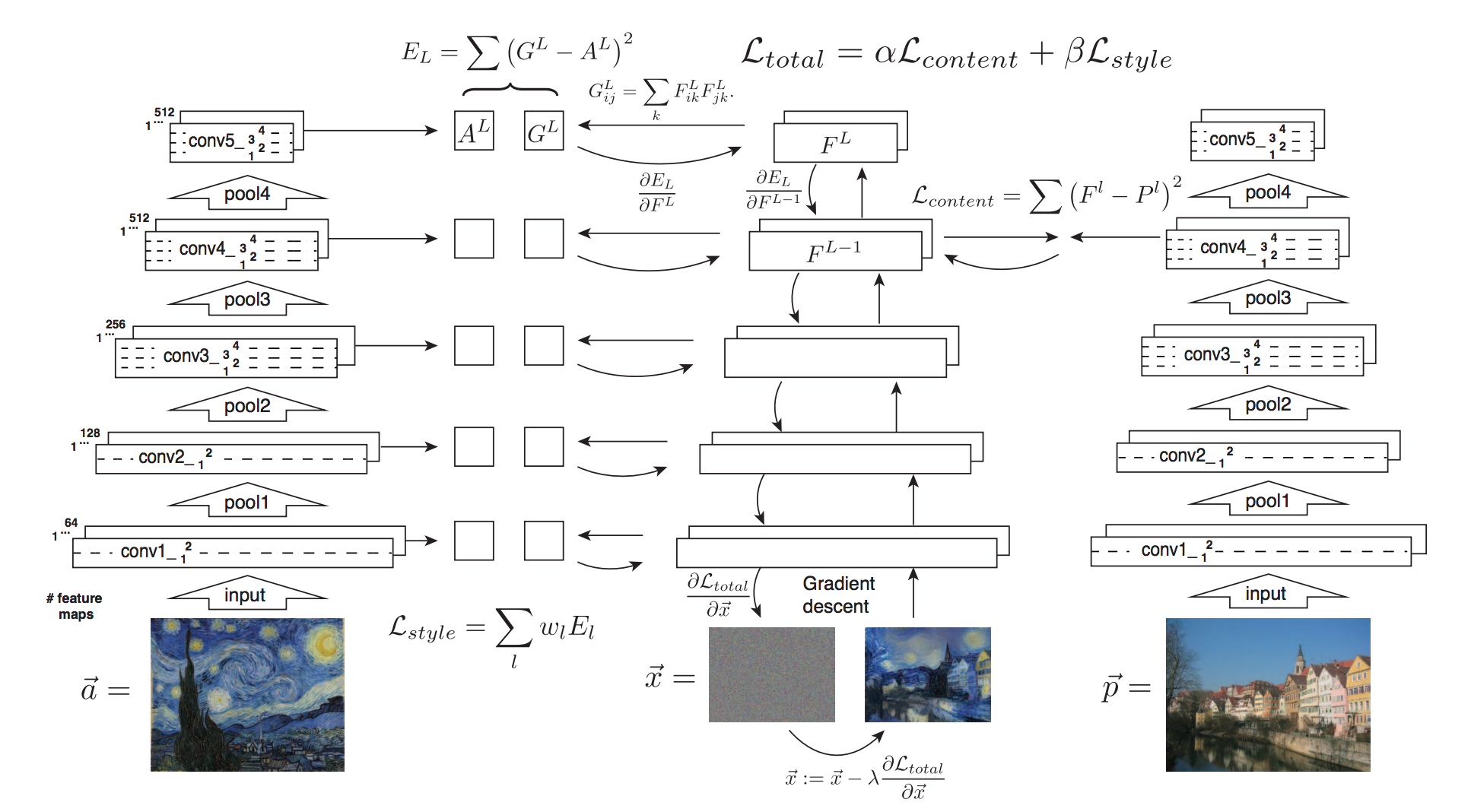
コンテンツ画像とスタイル画像への近さを測るために，2つの誤差を定義します．

コンテンツ誤差
$l$ 層目の $i$ 番目のチャネルの $j$ 番目のホワイトノイズの中間特徴を $F_{ij}^{l}$ で表します．
同様にコンテンツ画像の中間特徴を $P_{ij}^{l}$ とします．
コンテンツ画像とホワイトノイズ画像の中間特徴の二乗誤差を $L_{\rm content}$ とします．

L_{\rm content} = \frac{1}{2} \sum_{i, j} (F_{ij}^{l} - P_{ij}^{l})^{2}

深い層ほどピクセルの詳細な情報は失われ，物体の大まかな情報が抽出されます．
大体の位置や形状が保存されていればいいので，コンテンツ誤差は深い層で計算します．

スタイル誤差
スタイル画像の中間特徴のグラム行列を計算します．
グラム行列はチャネル間の相関を計算したものです．
各層のグラム行列を復元すると，深い層ほど大まかなパターンを捉えていることが分かります．

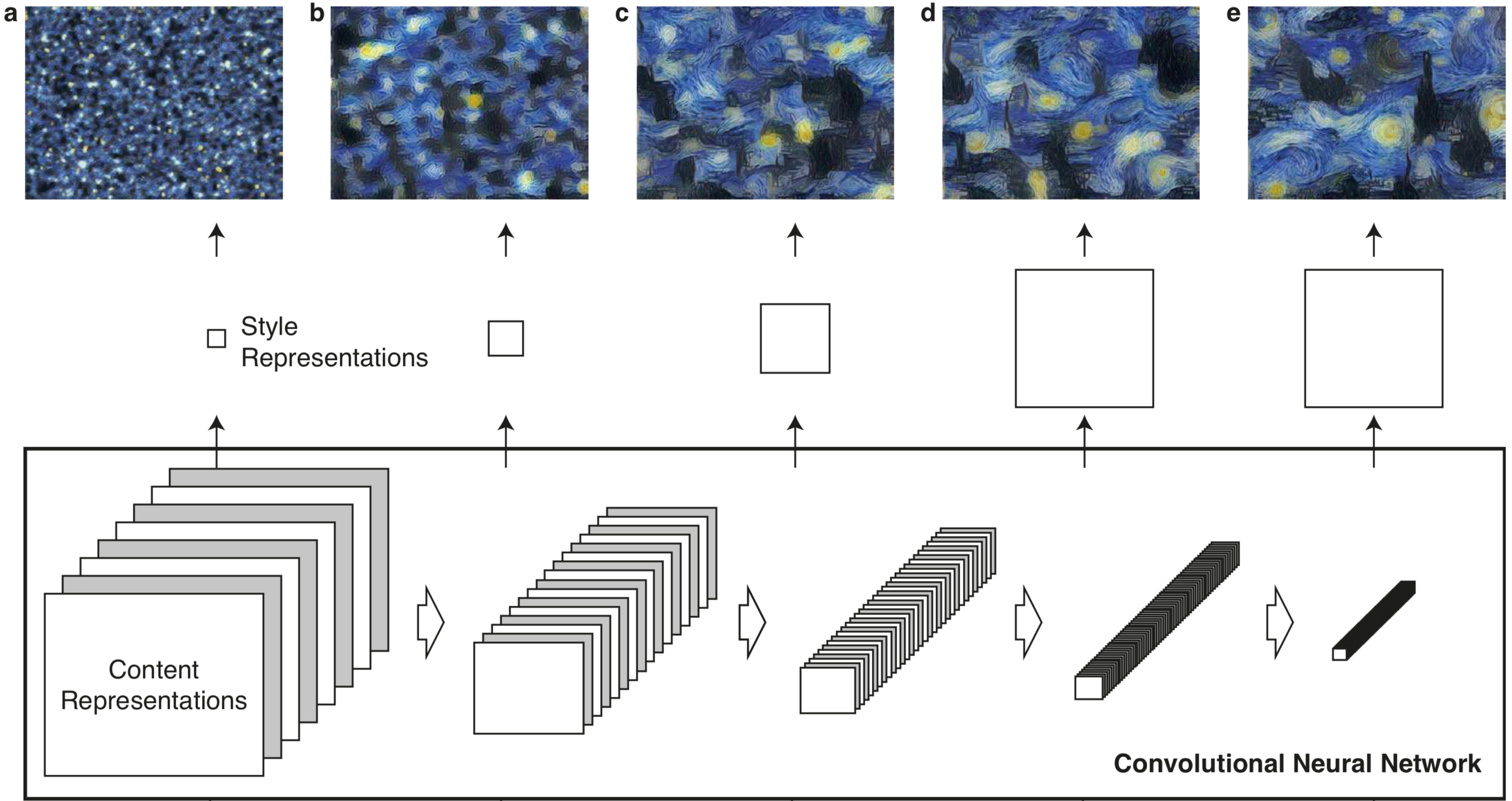
では，スタイル誤差の計算方法を説明します．
$l$ 層目の $i$ 番目の特徴ベクトルを $F_{i}^{l}$ とします．
$i$ 番目と $j$ 番目の特徴ベクトルの内積を $G_{ij}^{l}$ で表します．

G_{ij}^{l} = \sum_{k} F_{ik}^{l} F_{jk}^{l}

スタイル画像とホワイトノイズのグラム行列 $G_{ij}^{l}, A_{ij}^{l}$ の二乗誤差を $E_{l}$ とします．

E_{l} = \frac{1}{4 N_{l}^{2} M_{l}^{2}} \sum_{i, j} (G_{ij}^{l} - A_{ij}^{l})^{2}

パターンは細かいものから大まかなものまで取りたいので，
各層で計算した $E_{l}$ の重み付き和をスタイル誤差 $L_{\rm style}$ とします．

L_{\rm style} = \sum_{l} w_{l} E_{l}

最適化
$L_{\rm total} = \alpha L_{\rm content} + \beta L_{\rm style}$ を最小化します．
$\alpha, \beta$ はコンテンツ誤差とスタイル誤差のどちらの比重を大きくするかの係数です．
$\beta$ に対して $\alpha$ を小さくすると，物体の位置や形状が失われ画風が強く反映されます（左上）
逆に $\alpha$ を大きくすると，物体の位置や形状が保たれますが画風があまり反映されません（右下）
図の上の数字は $\alpha / \beta$ です．

Perceptual Losses for Real-Time Style Transfer and Super-Resolution

J. Johnson et al. ECCV 2017
コンテンツ画像とスタイル画像に近い変換画像 $\hat{y}$ を出力するように Image Transform Net $f_{W}$ を訓練します．
下図のようにGatysらの手法の前段に $f_{W}$ を配置した構造をしています．
$f_{W}$ が訓練対象であり，VGG-16は固定して使います．
$f_{W}$ を使って1回のforwardでスタイルを変換できるので，Gatysの手法より計算コストが低くなっています．
1つのスタイル画像でネットワークを訓練するため，学習に使ったスタイル画像の画風にしか変換できません．

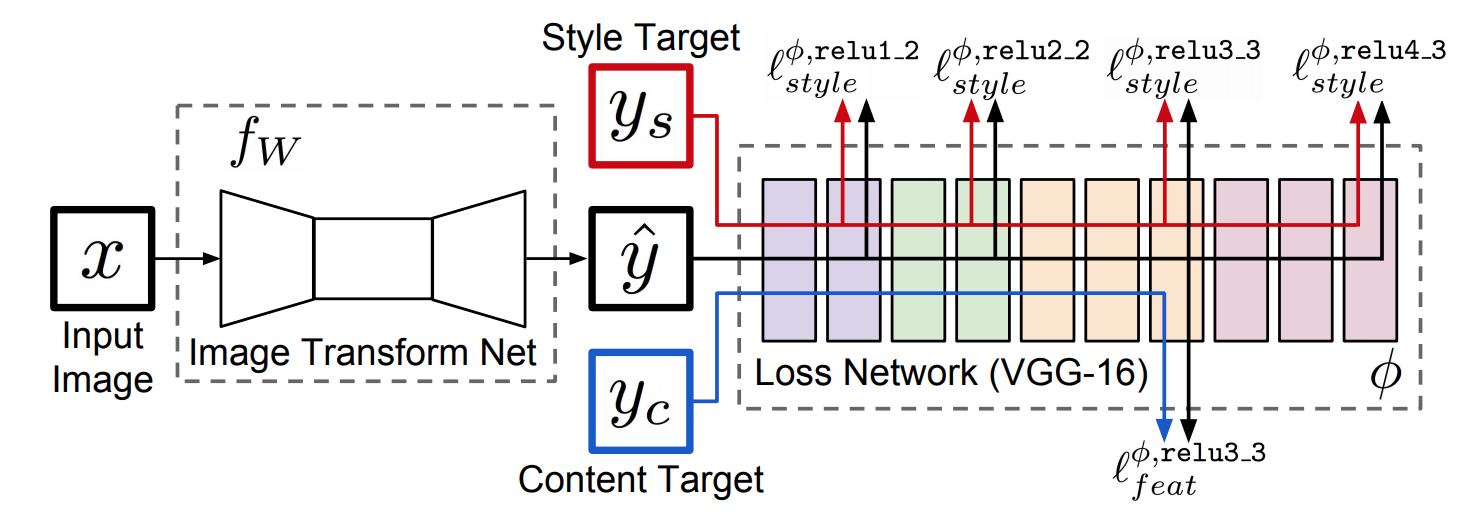
コンテンツ画像とスタイル画像への近さを測るために，2つの誤差を定義します．

Feature Reconstruction Loss
変換画像とコンテンツ画像それぞれの中間特徴の平均二乗誤差(MSE)を取ります．
$x$ を入力した時の $j$ 層目の特徴マップを $\phi_{j}(x)$ で表します．
チャネル数 $C_{j}$，特徴マップの高さ $H_{j}$ と幅 $W_{j}$ で割って平均をとっています．

l_{\rm feat}^{\phi, j}(\hat{y}, y_{c}) = \frac{1}{C_{j} H_{j} W_{j}} \|\phi_{j}(\hat{y}) - \phi_{j}(y_{c})\|_{2}^{2}

Style Reconstruction Loss
まず，変換画像とスタイル画像それぞれの中間特徴のグラム行列を計算します．
$j$ 層目の特徴マップ $\phi_{j}(x)$ のチャネル $c$ と $c'$ の要素積の合計を
特徴マップのサイズ $C_{j} H_{j} W_{j}$ で割ったものがグラム行列の $(c, c')$ 成分になります．

G_{j}^{\phi}(x)_{c, c'} = \frac{1}{C_{j} H_{j} W_{j}} \sum_{h = 1}^{H_{j}} \sum_{w = 1}^{W_{j}} \phi_{j}(x)_{h, w, c} \phi_{j}(x)_{h, w, c'}

次に，グラム行列のフロべニウスノルムを取ります．
フロベニウスノルムは行列の各要素の二乗和のルートをとって計算します．
パターンは細かいものから大まかなものまで取りたいので，各中間層での誤差を合計します．

l_{\rm style}^{\phi, j}(\hat{y}, y_{s}) = \|G_{j}^{\phi}(\hat{y}) - G_{j}^{\phi}(y_{s})\|_{F}^{2} \\
\|A\|_{F} = \sqrt{\sum_{i, j} a_{ij}^{2}}

A Learned Representation For Artistic Style

V. Dumoulin et al. ICLR 2017
Gatysらの手法とJohnsonらの手法は計算コストと変換可能なスタイル数のトレードオフでした．
Dumoulinらの手法は計算コストを抑えたまま，1つのモデルで複数のスタイルへの変換を可能にしています．
下図のようにStyle transfer networkにコンテンツ画像を入力し変換画像を得ます．
Style transfer networkは画風を学習しているので，変換時にはコンテンツ画像だけを入力します．
学習時には変換画像がコンテンツ画像とスタイル画像に近づくようネットワークを訓練します．
後段のVGG-16は学習済みのものを固定したまま使います．

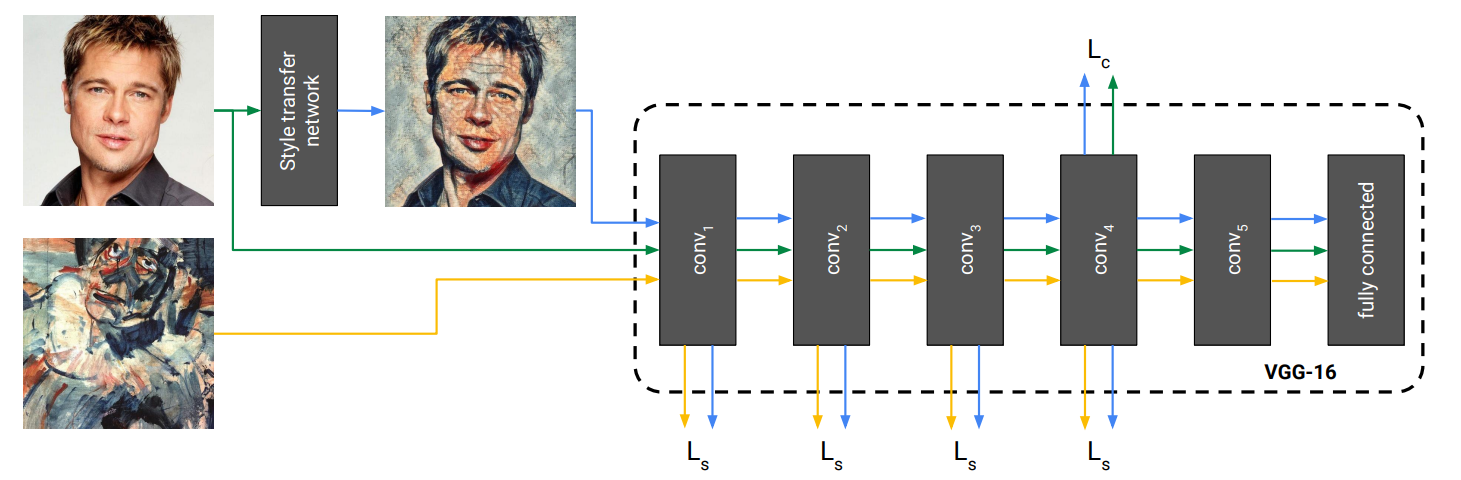
Style transfer networkでは中間特徴をサンプルごとチャネルごとに正規化します．
この正規化をInstance Normalization(IN)と呼びます．
INは以下のステップを踏みます．

1. 中間特徴 $x$ のチャネルごとの平均 $\mu$ と分散 $\sigma$ を求める
2. $\mu, \sigma$ を使って正規化し $x_{\rm norm}$ を得る
3. $x_{\rm norm}$ をパラメータ $\beta_{s}, \gamma_{s}$ で変換する

$\beta_{s}, \gamma_{s}$ はスタイル画像ごとに学習したINの変換パラメータです． 図のように変換したい画風 $s$ のパラメータを使って変換します． 論文では32個のスタイル画像を使って学習し，32パターンの変換を実現しています． $\beta_{s}, \gamma_{s}$ はスタイル画像ごとに学習するので，学習していないスタイルへの変換はできません． 異なるスタイル画像で学習したINパラメータを任意の比率で足し合わせると， 中間のスタイルへの変換することができます．

\beta = \alpha \cdot \beta_{1} + (1 - \alpha) \cdot \beta_{2} \\
\gamma = \alpha \cdot \gamma_{1} + (1 - \alpha) \cdot \gamma_{2}

以下の図は4つのスタイル画像を使って中間のスタイルへ変換した例です．

Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization

X. Huang et al. ICCV 2017
Dumoulinらの手法は学習していないスタイルへ変換できませんでした．
1つのモデルであらゆるスタイルへの変換を可能にしたのがAdaptive Instance Normalization(AdaIN)です．
訓練対象はDecoderの部分で，VGGは学習済みのモデルを固定して使います．
スタイル画像を使って学習をしていますが，学習に使っていないスタイル画像でも変換が可能です．

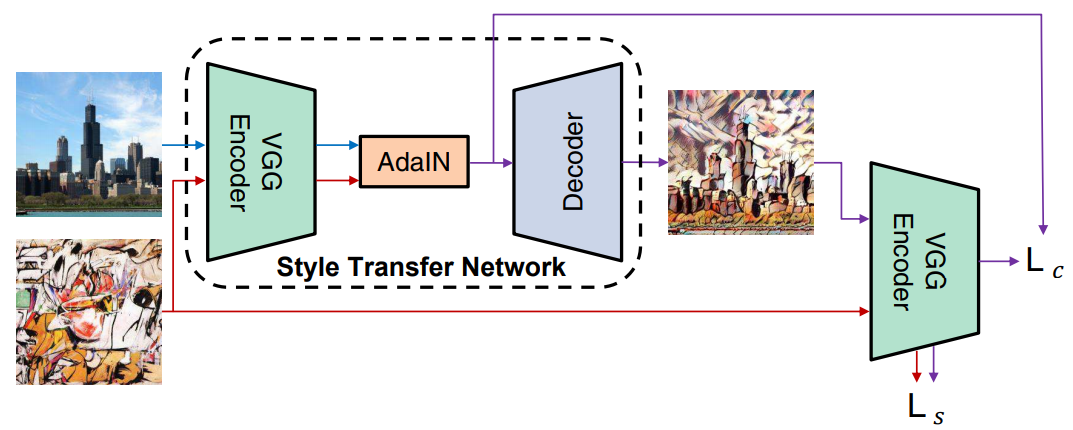
AdaINは以下のステップを踏みます．

1. コンテンツ画像の中間特徴 $x$ のチャネルごとの平均 $\mu(x)$ と分散 $\sigma(x)$ を求める
2. 同様にスタイル画像の中間特徴 $y$ から $\mu(y), \sigma(y)$ を求める
3. $\mu(x), \sigma(x)$ を使って $x$ を正規化
4. 正規化した特徴を $\mu(y), \sigma(y)$ で変換

3, 4の処理は以下のように計算できます．

z = \sigma(y) \left(\frac{x - \mu(x)}{\sigma(x)}\right) + \mu(y)

Dumoulinらの手法と比較すると，スタイルごとに学習した変換パラメータ $\beta_{s}, \gamma_{s}$ を，
スタイル画像の中間特徴の平均 $\mu(y)$ と分散 $\sigma(y)$ に置き換えた形になります．
変換した特徴 $z$ から変換画像を生成するようDecoderを訓練します．
これまでの手法と同じようにコンテンツ誤差とスタイル誤差を定義します．

コンテンツ誤差
AdaINの出力を $t$，変換画像を $g(t)$ とします．
変換画像をVGG Encoderに入力した結果 $f(g(t))$ と $t$ の距離をコンテンツ誤差とします．

L_{c} = \|f(g(t)) - t\|_{2}

スタイル誤差
スタイル誤差は，変換画像とスタイル画像それぞれの中間特徴の平均と分散を近づけるように設定します．
論文によるとグラム行列を用いても同じような結果になるとのことです．

L_{s} = \sum_{i = 1}^{L} \|\mu(\phi_{i}(g(t))) - \mu(\phi_{i}(s))\|_{2} + \sum_{i = 1}^{L} \|\sigma(\phi_{i}(g(t))) - \sigma(\phi_{i}(s))\|_{2}

中間スタイルへの変換
コンテンツ画像は固定したまま，複数のスタイル画像を使ってAdaINの出力を得ます．
この出力を任意の比率で足し合わせると，中間のスタイルへ変換した結果が得られます．

Universal Style Transfer via Feature Transforms

Y. Li et al. NIPS 2017
これまでの手法はスタイル画像を使った学習が必要でした．
この手法はwhitening and coloring(WCT)により，スタイル画像での学習は不要です．
非常にシンプルな手法ですが，良い結果が得られる印象です．

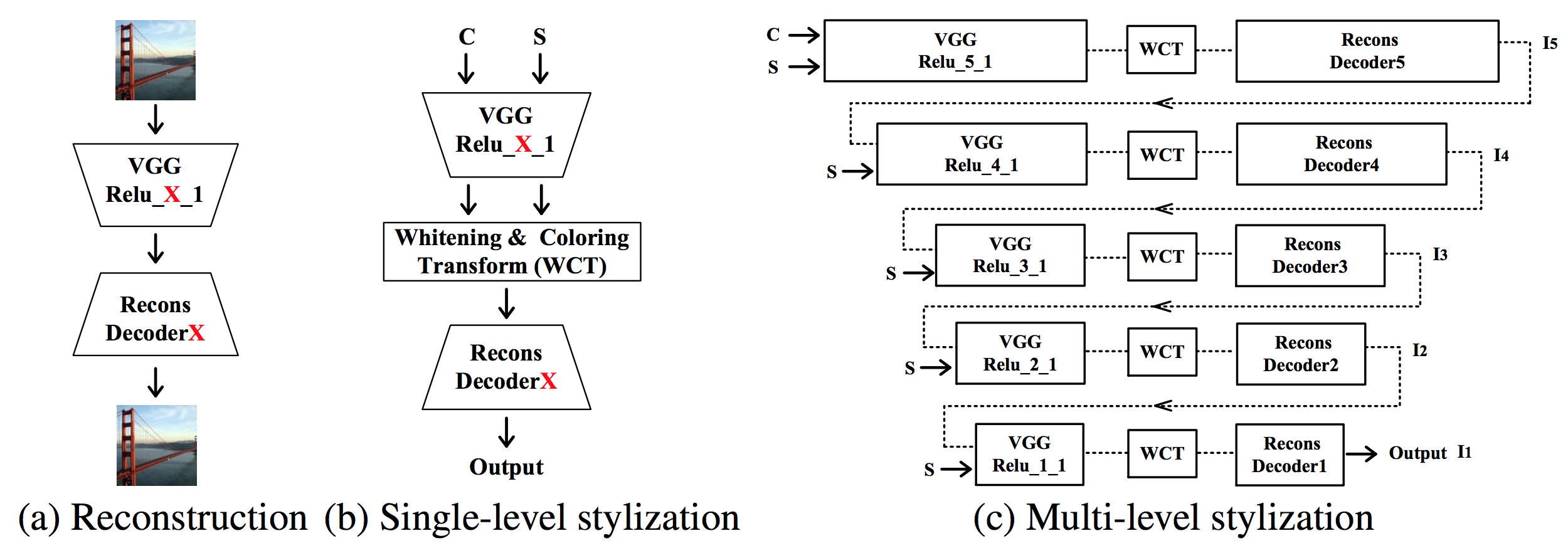
VGGネットワークを使ったAuto Encoderの間にWCTのレイヤーを入れます．
WCTのレイヤーでは以下の処理をします．

1. コンテンツ画像の中間特徴を白色化(whitening)
2. スタイル画像の中間特徴の固有値固有ベクトルで1の結果を変換(coloring)
3. 2の結果をDecoderに入力して変換画像を得る
4. 変換画像をコンテンツ画像としてこれまでの処理を繰り返し

whitening
コンテンツ画像の中間特徴を白色化します．
白色化により物体の構造情報を保ったまま画風の情報を削ぎ落とすことができます．
$D_{c}$ は対角成分に固有値を並べた行列，$E_{c}$ は固有ベクトルを並べた行列，$m_{c}$ は平均ベクトルです．

\hat{f}_{c} = E_{c} D_{c}^{- \frac{1}{2}} E_{c}^{T} (f_{c} - m_{c})

coloring
白色化した特徴をスタイル画像のパラメータで変換します．
$D_{s}$ は対角成分に固有値を並べた行列，$E_{s}$ は固有ベクトルを並べた行列，$m_{s}$ は平均ベクトルです．

\hat{f}_{cs} = E_{s} D_{s}^{\frac{1}{2}} E_{s}^{T} f_{s} + m_{s}

中間スタイルへの変換
Dumoulin, Huangらの手法ではNormalizationの変換パラメータを任意の比率で足し合わせて，
中間スタイルへの変換を実現していました．
Liらの手法では，変換した特徴 $\hat{f}_{cs}$ 自体を任意の比率で足し合わせます．

\hat{f}_{cs} = \beta \hat{f}_{cs_{1}} + (1 - \beta) \hat{f}_{cs_{2}}

Fast Patch-based Style Transfer of Arbitrary Style

T. Q. Chen et al. NIPS 2016
これまでの手法はスタイル画像のパラメータを使ってコンテンツ画像の中間特徴を変換していました．
Chenらの手法はコンテンツ画像の中間特徴をスタイル画像の中間特徴で置換します．
論文ではこの置換をStyleSwapと呼んでいます．

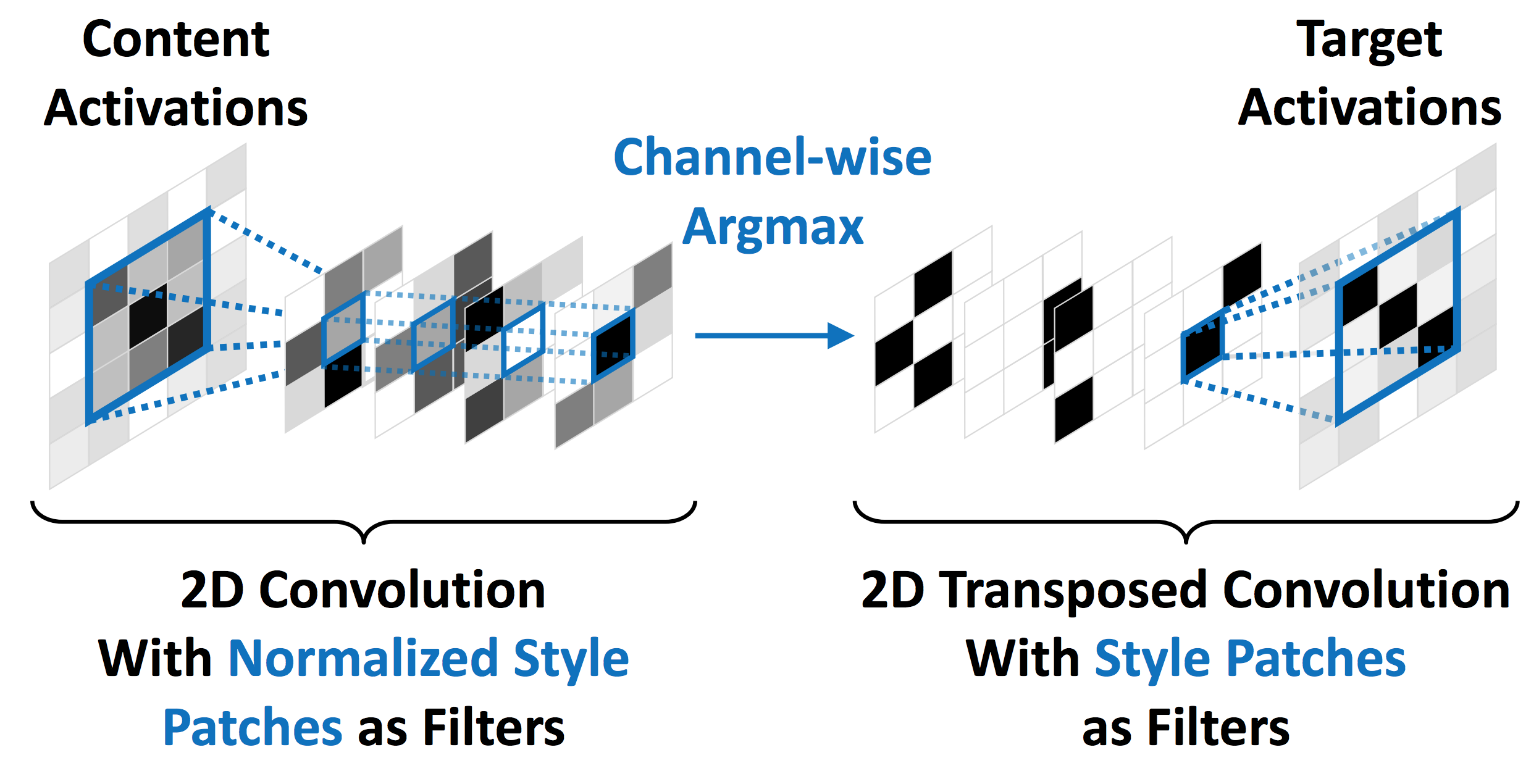
コンテンツ画像とスタイル画像それぞれの中間特徴をパッチに切り出し，
パッチ間のコサイン類似度が最大のもので置換します．

\phi_{i}^{ss}(C, S) = \arg{\max_{\phi_{j}(S), j = 1, \cdots, n_{s}}} \frac{\langle\phi_{i}(C), \phi_{j}(S)\rangle}{\|\phi_{i}(C)\| \cdot \|\phi_{j}(S)\|}

置換した特徴を復元することで変換画像を得ます．

Avatar-Net: Multi-scale Zero-shot Style Transfer by Feature Decoration

L. Sheng et al. CVPR 2018
AvatarNetはWCTとStyleSwapを組み合わせた手法です．
以下のステップでスタイルを変換します．

1. コンテンツ画像の中間特徴を白色化
2. スタイル画像の中間特徴を白色化
3. 白色化した特徴間でコサイン類似度が最大のものに置換
4. 3の結果をスタイル画像の中間特徴の固有値固有ベクトルで変換

WCTの途中でStyleSwapをはさむことでスタイル画像のパターンを自然に反映することができます．
Liらの手法と同様に，変換した特徴を任意の比率で足し合わせることで中間スタイルへ変換できます．

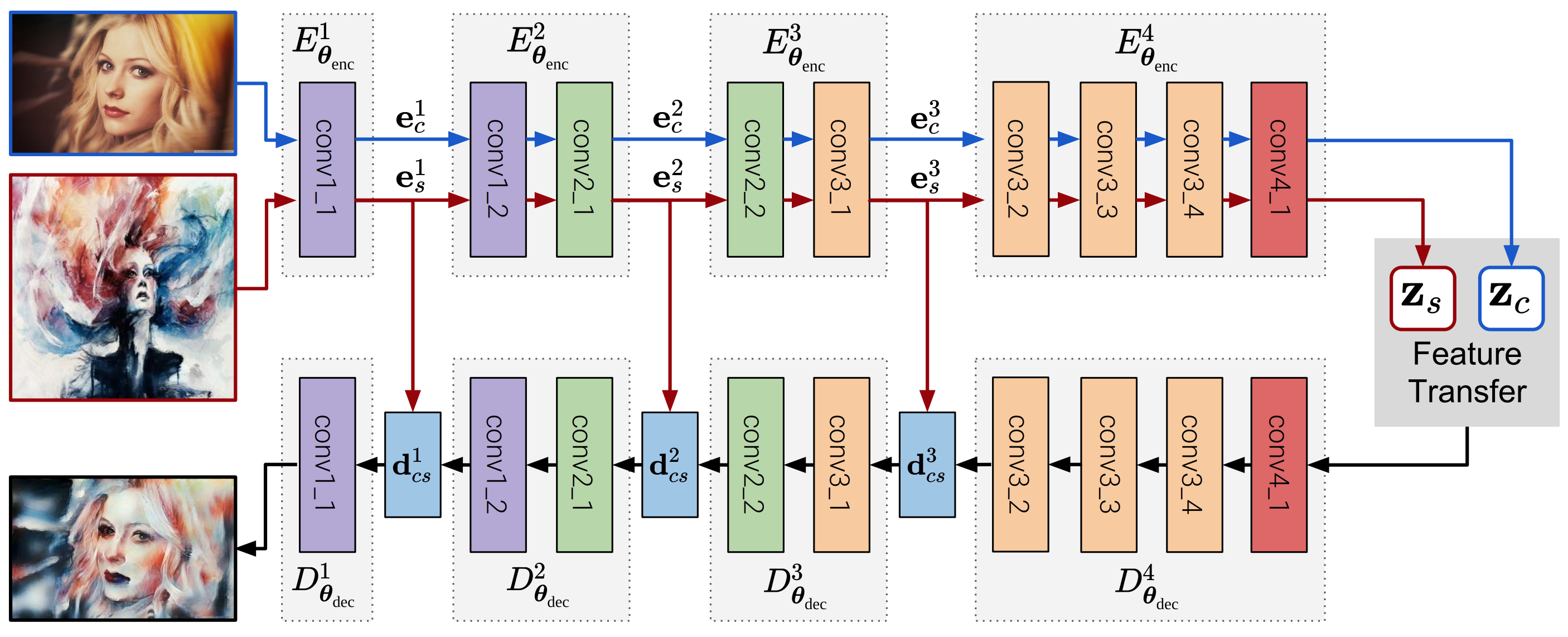
論文ではAdaIN, WCT, StyleSwap, AvatarNetの中間特徴の変換方法を図で比較しています．

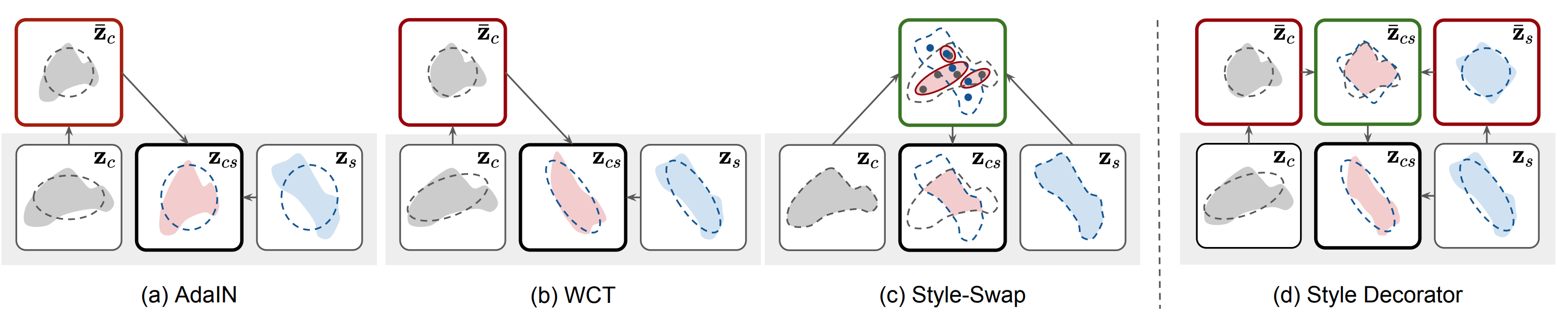
手法	特徴の変換方法
AdaIN	平均と分散をスタイル画像に揃える
WCT	平均と分散共分散をスタイル画像に揃える
StyleSwap	コサイン類似度が最大の特徴で置き換え
AvatarNet	コサイン類似度が最大の特徴で置き換えてから平均と分散共分散をスタイル画像に揃える

References

1. L. A. Gatys, A. S. Ecker, and M. Bethge. Image style transfer using convolutional neural networks. In CVPR, 2016. ↩

2. J. Johnson, A. Alahi, and L. Fei-Fei. Perceptual losses for real-time style transfer and super-resolution. In ECCV, 2016. ↩ ↩² ↩³

3. V. Dumoulin, J. Shlens, and M. Kudlur. A learned representation for artistic style. In ICLR, 2017. ↩

4. X. Huang and S. Belongie. Arbitrary style transfer in realtime with adaptive instance normalization. In ICCV, 2017. ↩ ↩² ↩³

5. Y. Li, C. Fang, J. Yang, Z. Wang, X. Lu, and M.-H. Yang. Universal style transfer via feature transforms. In NIPS, 2017. ↩

6. L. Sheng, Z. Lin, J. Shao, and X. Wang. Avatar-net: Multi-scale zero-shot style transfer by feature decoration. In CVPR, 2018. ↩ ↩² ↩³ ↩⁴

7. T. Q. Chen and M. Schmidt. Fast patch-based style transfer of arbitrary style. arXiv:1612.04337, 2016. ↩