お手軽にランダムなIDを取得したい時にUUIDはとても重宝します。
でもたまに、
「このID(UUID)ってぶつかることない?対策しなくて大丈夫?」
と聞かれることがあります。
それに対して、
「ウィキペディア先生がぶつからねえって言ってたから大丈夫だよ!(#゚Д゚)」
で切り抜けるのもそろそろ限界のような気がするのでちゃんと調べました。
(もちろんウィキペディア先生を頼りました!)
2つの理論
UUIDの衝突確率について考える上で次の2つの理論が重要になります。
- 鳩の巣原理
- 誕生日のパラドクス
鳩の巣原理
鳩の巣原理とは、
m個の入れ物にn個のものを入れるとき、n > m ならば少なくとも1個の箱には2個以上のものが入る
9個の巣箱に10羽の鳩が入る場合、必ずどれかの巣箱には2羽以上入ることになるということです!(ウィキペディア先生)
考えれば当たり前のことですが同様にして考えれば、
「1..100の乱数生成を101回した場合必ず1回以上同じ値が出る」
ということなのでハッシュやUUIDの衝突確率にも応用できます。
衝突する確率は数式で一般化できますが割愛。
「箱の数が十分でなければぶつかりうる」ということだけ覚えておいてください。
誕生日のパラドクス
続けて誕生日のパラドクスです。これは、
1クラスに23人いるとき同じ誕生日のペア(以上)が存在する確率は50%以上
になるという理論です。
「365日もあるのに思ったより確率が高い」
と思ったでしょうか?このことからパラドクスと呼ばれています。
この確率が正しいかは先ほどの鳩の巣原理の応用になります。
鳩の巣原理より1クラスに366人いる場合(多い!)、同じ誕生日のペア以上が存在する確率は100%です。(うるう年でない場合)
確率を数式化してみます。
まず、n人全員の誕生日が異なる確率を求めます。
最初に、2人のとき、誕生日が同じになる確率は 1/365 なので誕生日が異なる確率は
1-(1/365) = 364/365 ・・・②
同様に、3人目の誕生日が異なる確率は
1 - ((1/365)+(1/365)) = 363/365 ・・・②
つまり、3人の誕生日が全て異なる確率は① * ②より
(364/365) * (363/365) = (364*363)/365^2≒0.991795834..
これを一般化すると
(364/365) * (363/365) * (362/365) * ... * ((365-n+1)/365) = 365!/(365^n-(365-n)!)
この確率を1から引けば少なくとも2人以上が同じ誕生日である確率になります。
1 - 365!/(365^n-(365-n)!)
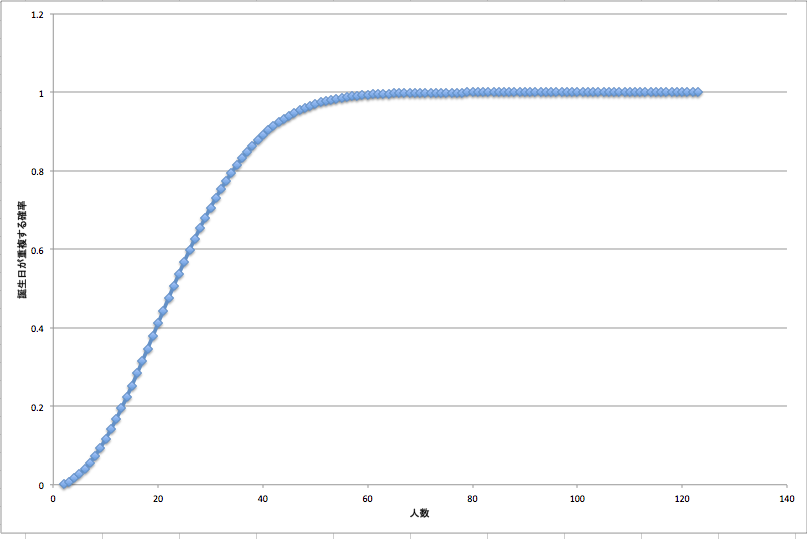
n=23のときに確率は0.507となり50%を超えます。
せっかくなのでコード化
memo = {} # 計算量削減のためのメモ化
def _birthday_conflict(n):
"""
n人目の誕生日が異なる確率
"""
if n in memo:
return memo[n]
else:
rate = (365.0-n)/365.0
memo[n] = rate
return rate
def birthday_conflict(n):
"""
n人の誕生日が全て異なる確率
"""
rate = 1.0
for i in range(1, n):
rate *= _birthday_conflict(i)
return rate
def not_birthday_conflict(n):
"""
n人の少なくとも2人が同じ誕生日になる確率
"""
return 1.0 - birthday_conflict(n)
# 実際に計算
[(n, not_birthday_conflict(n)) for n in range(2, 365)]
23人で0.507...と50%を超え、119人で100%に収束します。
ついでに、n人いる教室に入室した場合、自分と同じ誕生日の人がいる確率を求めてみます。
まず、ある人が自分と同じ誕生日でない確率は 364/365
これがn人に対し同時に起こりうる確率は
(364/365)^n
つまり同じ誕生日の人が少なくとも1人いる確率は
1-(364/365)^n
となります。
コードは
def not_same_birthday(n):
return 1.0 - (364.0/365.0)**n
と単純です。結果は、
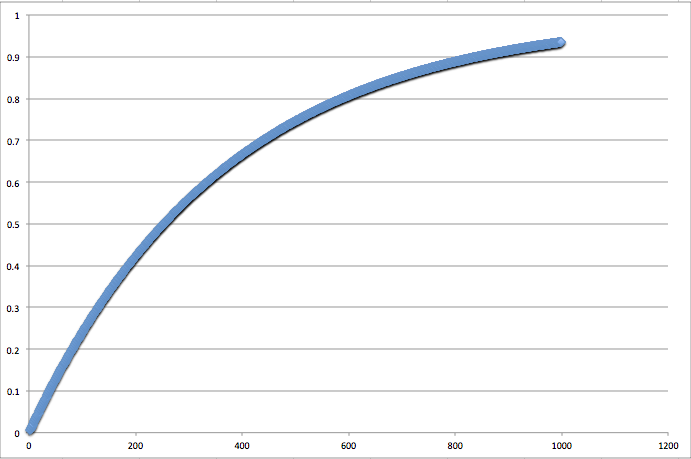
と先ほどと打って変わって253人でようやく50%を超えます。
誕生日攻撃
長々とやってきましたが、誕生日のパラドクスは誕生日攻撃と呼ばれる攻撃手法の基になっている理論です。(ここから難しいのでウィキ先生頼り)
乱数をひたすら作って同じものが出るまで繰り返すという単純な方法ですが、誕生日のパラドクスの通り、意外と回数は少なくて済んでしまいます。
H個の異なる出力をそれぞれ同じ確率で生成した場合、同じ結果が出るまでの回数は平均
1.25*√(H)
回だそうです。
(誕生日の場合のH=365で23.88回と出るので妥当性がわかります)
これを数式で近似やら色々やって最終的にN-ビットの乱数生成がぶつかるまでの回数の期待値を求めると、
2^{N/2}
回だそうです。
この式がほしかったものです。
結論
UUID(ver.4) は122ビットの乱数なので生成したUUIDが既存のものにぶつかるまでの回数の期待値は
2^{122/2} = 2305843009213693952回 = 2.3*10^{18}
230京回となります。
これはぶつからない!