概要
自学の為、過去に学習した時系列分析理論の基礎を整理していきたい
はじめは、厳密性よりは全体的な地図を描けるよう、粗い粒度から進めてみたいと思う
(コンパクトな構成にするため、コードは最小限)
(https://zenn.dev/t_shi/articles/7bc8787f4477b4 と同一です)
内容
時系列データの特徴を3行で
強引にまとめると
- データ生成過程DGPから、時間に従って変化する確率分布をモデル化する
- DGPから時点のデータが得られたと過程し、理論的な期待値や分散を求める
- 時系列データ =
短期の自己相関 + 周期的変動 + トレンド + 外因性 + ホワイトノイズ
t時点におけるデータはたった一点しかないが、それは、時点における確率分布の中から、得た一点であると仮定する
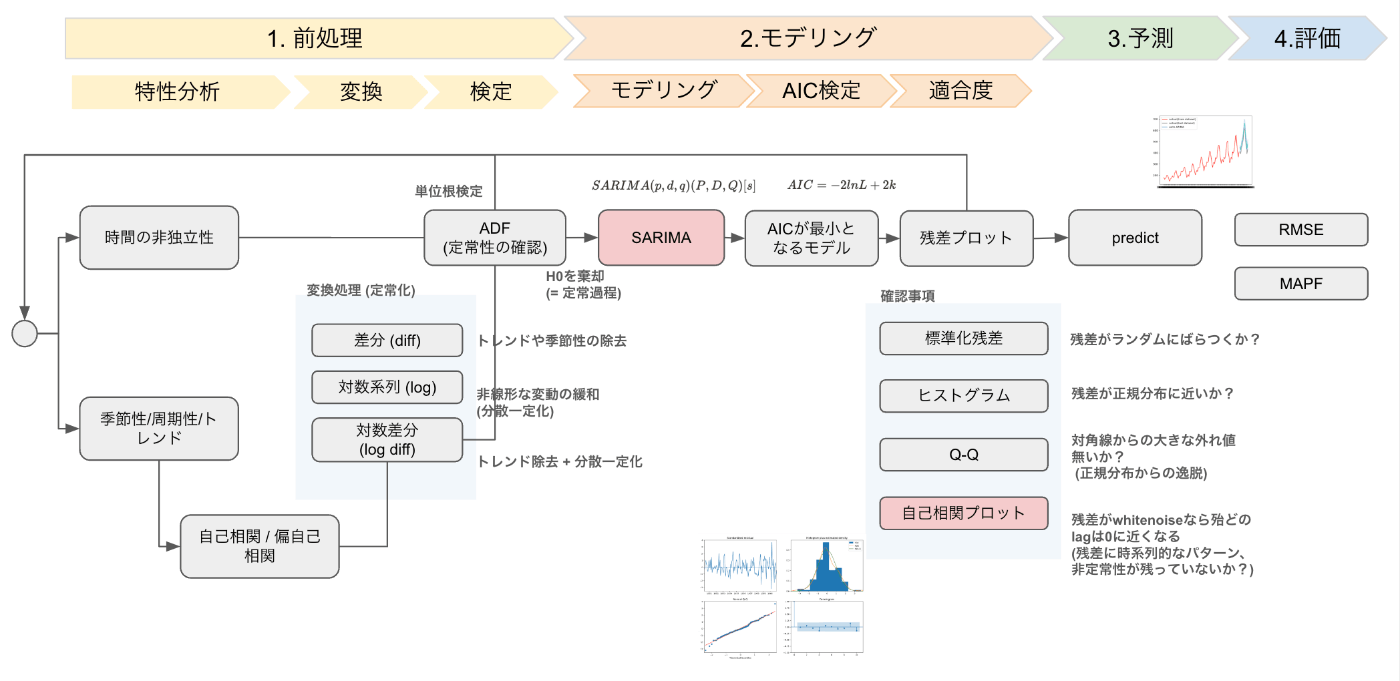
先ずは一通り試してみる際のイメージ
- 前処理 = 自己相関, 偏自己相関分析 / 定常化変換処理 (diff, log) / ADFによる単位根検定
- モデリング = 今回はSARIMA / AIC / 残差plotによる確認
- 予測
- 評価 = RMSE, MAPFなど
(2)に関して、一般に基礎理論の記事では、AR, MA, ARIMA, SARIMAと順を追って説明する事が多いが
記事としてのコンパクトさを優先した結果として、いきなりSARIMAで進めることにした
(VARやProphetは割愛)
SARIMA
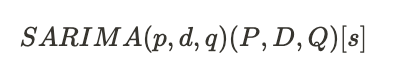
一周期がsであるデータにおいて、(月単位ならs=12)ARIMAの次数(p,d,q)及び、季節性の次数(P,D,Q)を指定する
ざっくりと、SARIMAモデルまでの変遷
- AR = 自己回帰モデル
- MA = 移動平均モデル
- ARMA = (1)+(2)。定常データに使える、非定常には使えない
- ARIMA = (3)を非定常でも利用できるよう、差分系列をとって、定常過程に変換してからARMAモデルを使う
- SARIMA = ARIMA + 季節性成分
実際に動かしてみる
データは Kaggle - Air Passengersを使用
1. 前処理
非定常過程が定常過程になるように、変換処理を施す
| # | 原系列 | 差分系列 | 対数系列 | 対数差分系列 |
|---|---|---|---|---|
| 処理 | * | diff | log | log + diff |
| Graph | 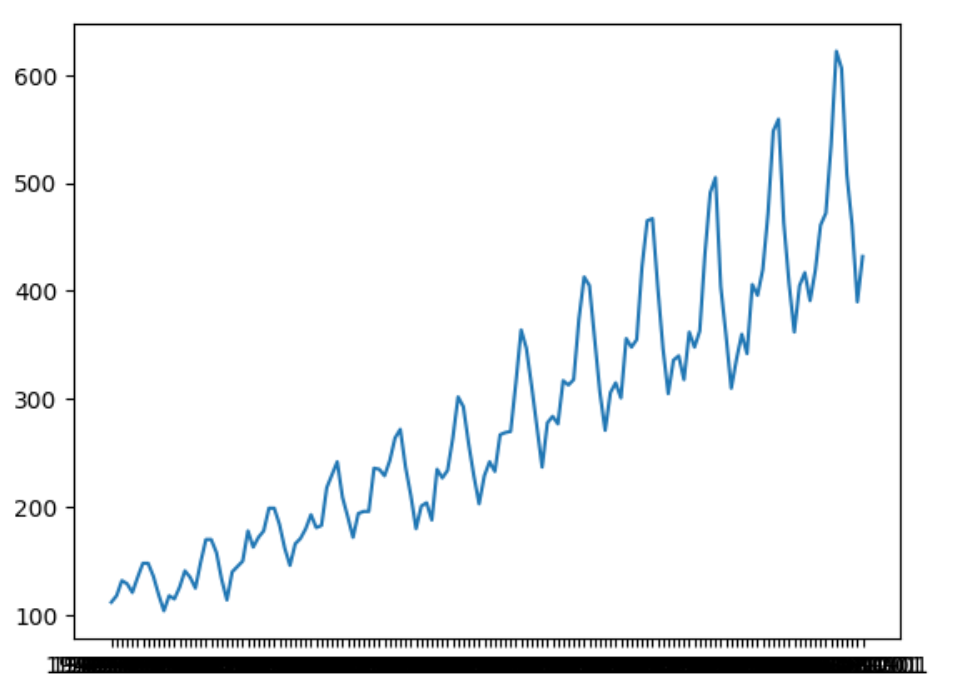 |
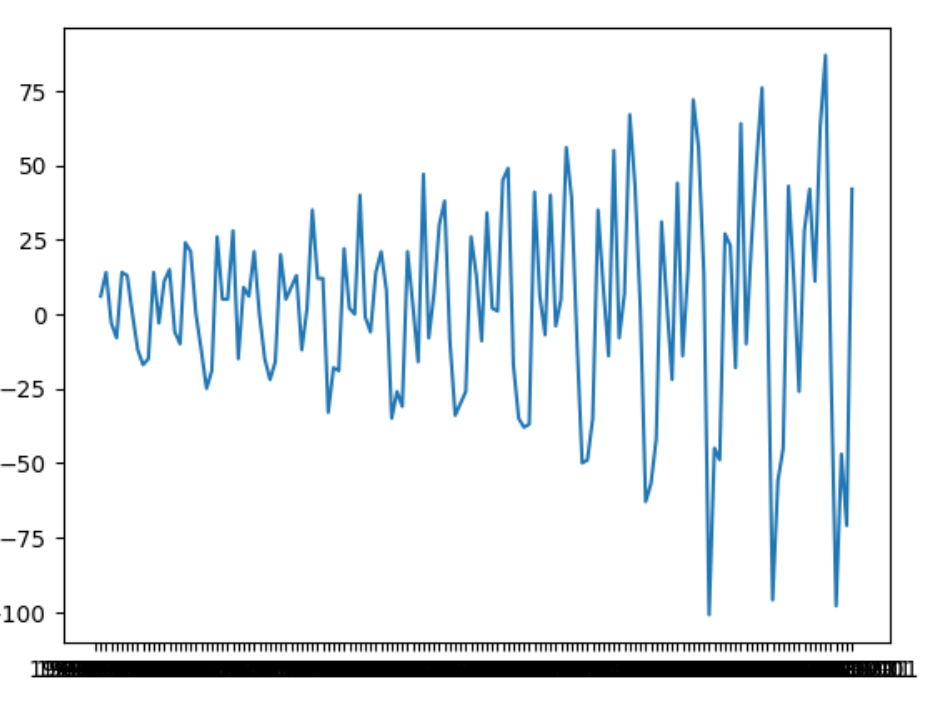 |
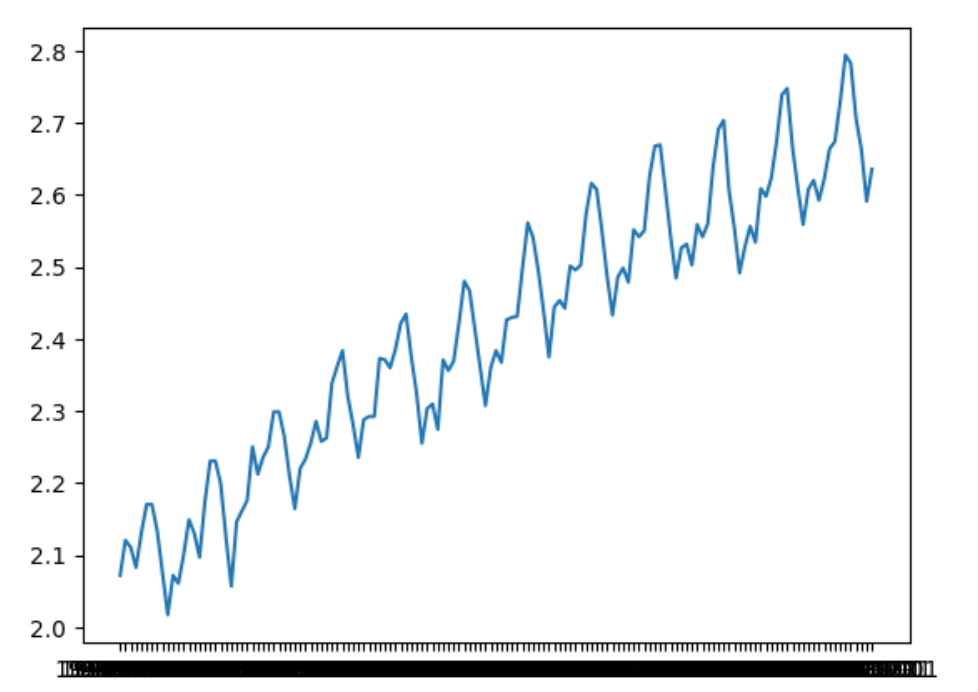 |
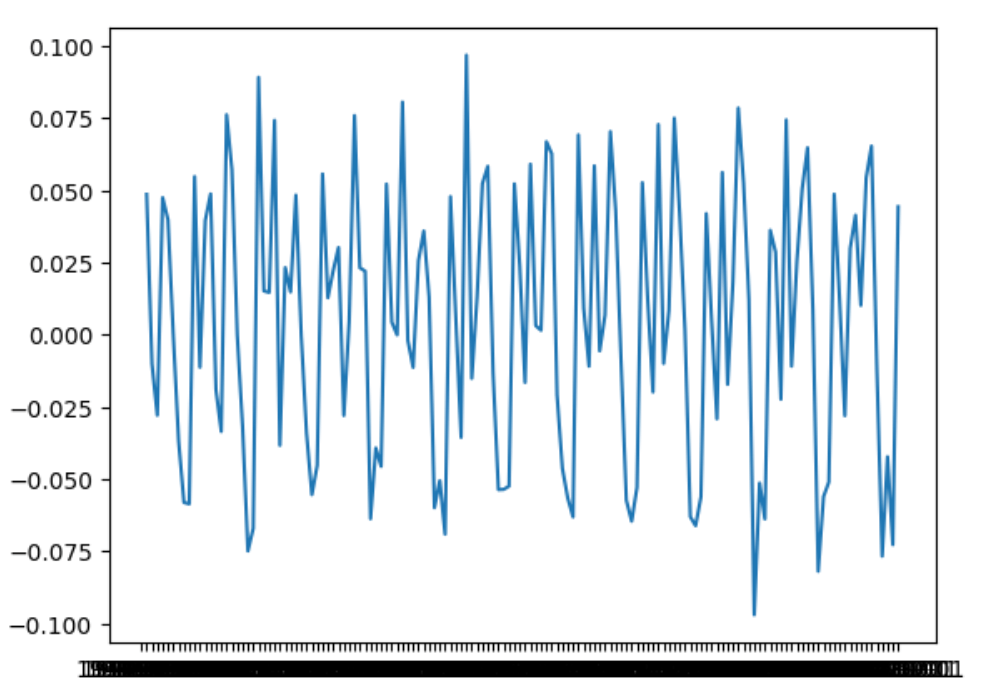 |
| ADF |  |
 |
 |
 |
| p値 | 0.99 | 0.054 | 0.416 | 0.048 |
右端の対数差分系列であれば、p値が0.048 (4.8%)でHo (帰無仮説)が棄却される
つまり、単位根は存在せず、定常過程とみなせる
今回は割愛しているが、その他、非定常な時系列データを定常化する処理として
- トレンド除去
- 差分化 = n期前データとの差分を取る
- Box-Cox変換 = Box-Coxは対数変換を一般化したもの
2. モデリング
SARIMAモデルのパラメータは、AICが最小化されるように自動判定する
(1)の過程に反し、改善の余地がある状況を明確に再現したい意図もあり
入力データは無変換のデータを利用する (= df["Passengers"])
import pmdarima as pm
arima_model = pm.auto_arima(df["Passengers"], seasonal=True, m=12, trace=True, n_jobs=-1, maxiter=10)
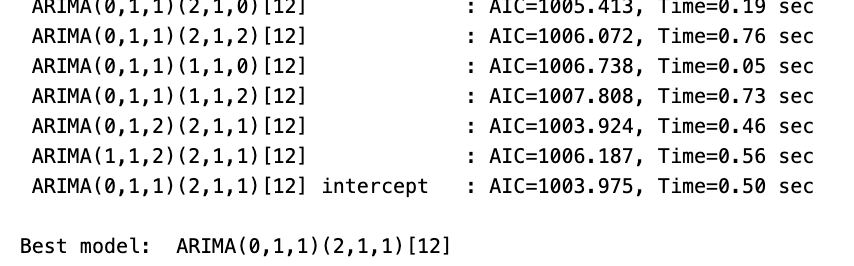
SARIMA(0,1,1)(2,1,1)[12]がベストと判定された
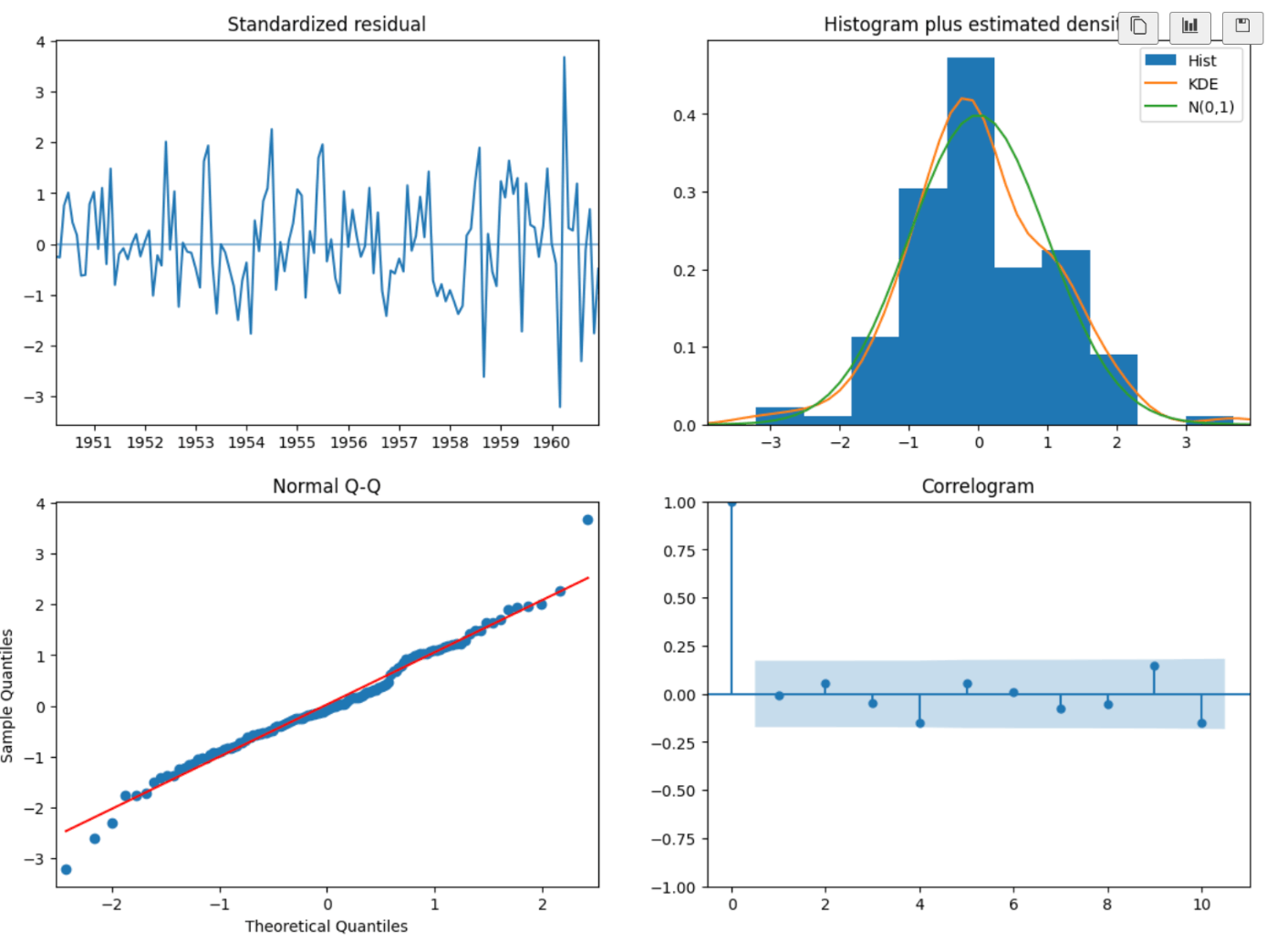
推定されたパラメータに対して、残差プロットをベースにモデルの適合度を検証する
arima_model.plot_diagnostics(figsize=(14,10))
- 残差はホワイトノイズに近く見えるが、一部外れ値がある
- 正規分布というより、やや左に傾いている
- コレログラムからlagは0から外れている箇所もあり、若干の周期性
が見受けられる (改善の余地が見受けられる)
3. 予測
予測値のグラフを書く
from pmdarima import model_selection
df_train, df_test = model_selection.train_test_split(df["Passengers"], test_size=12)
test_pred, test_pred_ci = arima_model.predict(n_periods=df_test.shape[0], return_conf_int=True)
plot_graph(df_train, df_test, test_pred, test_pred_ci) # 実装は省略
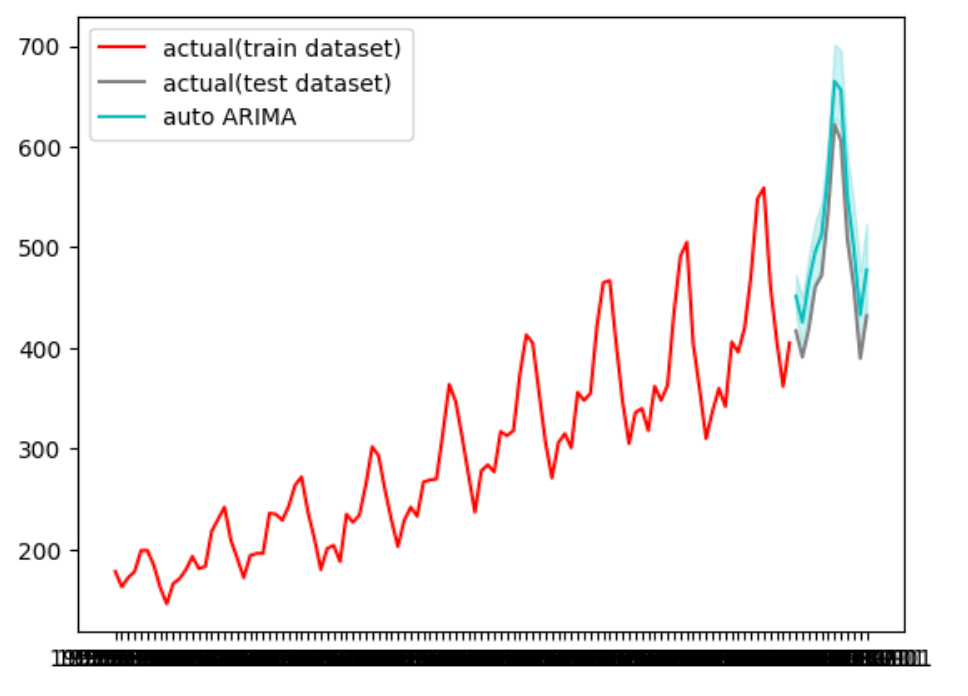
グラフの形状は学習できている印象はあるが、値が大きく上振れしている為、精度に課題がある事が分かる
4. 評価
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error
print(f"RMSE: {np.sqrt(mean_squared_error(df_test, test_pred))}")
print(f"MAPE: {np.sqrt(mean_absolute_percentage_error(df_test, test_pred))}")
# RMSE: 41.592855995849725
# MAPE: 0.2968483480823645
予測モデルの予測が、実際の観測値と比較して、平均して29%の誤差があるという状況は決して良くはない
改善余地がある為、変換処理等を再検討し、精度向上に努めていく
(当該ブログとしては、一旦ここまで)
参考
[ 書籍 ]
[ web ]
- セールスアナリティクス - (Python版)複数季節性を持つ時系列データをモデル化する方法(TBATSモデルとARIMAモデル)
- ROXX開発者ブログ - 時系列分析による時系列データの解析と未来予測(ARIMA, SARIMA)
- Time Series Forecasting with ARIMA , SARIMA and SARIMAX
総括
実用時に参照する全体像を掴める資料を作るのが目的なので、上澄みを掬った内容になっている点、ご容赦いただけますと幸いです
(数学を専門とする方にはお叱りを受けそう・・)
以上