この記事は「群知能と最適化2019 Advent Calender」7日目の記事です。
カオスとかAIWFとかかっこよくね?ということで調べて実装してみました。
概要
カオス粒子群最適化 (CPSO: Chaotic Particle Swarm Optimization) とは、メタヒューリスティックアルゴリズムの一つであるPSOにカオスを組み込んだ最適化アルゴリズムです。
他のPSOアルゴリズムと同様、多くの変形モデルがありますが、基となる論文は2005年に発表されました。
この記事ではCPSOをPythonで実装した上で、ベンチマーク関数で評価を行ったのでまとめます。
アルゴリズムと実装
CPSOは大まかに以下のような手順で実装していきます。
- PSOの実行(重みにおいてAIWF*を使用)
- 上位1/5のParticleを抽出
- 抽出したParticleに対してCLS*を行い、位置を更新
- CLSを行ったParticleの位置情報を基に探索範囲を削減
- 新しい探索範囲内で下位4/5のParticleをランダムに再生成
- 各Particleの評価を行い、停止条件を満たしていれば終了、満たしていなければ1.に戻る
*AIWF (Adaptive Inertia Weight Factor): 適応慣性荷重係数。PSOにおけるパラメータの一つである慣性係数に対する提案手法。
*CLS (Chaotic Local Search): カオス的局所探索。PSO実行後、局所探索のために用いる提案手法。
記事内では主要な部分だけコードを載せています。
全体のコードはGitHubで公開しています。
https://github.com/TatsukiSerizawa/Meta-heuristic/blob/master/cpso.py
1. PSOの実行
まず、PSOを実行します。
PSOは各粒子が現在の位置$x$と速度$v$を持ち、それらを更新していくことで最適解を探索します。移動にかかる各粒子の速度と位置は以下の式で更新されます。
$$
v_{id}(t+1) = w_{id}(t) + c_p × r_p × (pBest_{id} - x_{id}(t)) + c_g × r_g × (gBest_{id} - x_{id}(t))
$$
$$
x_{id}(t+1) = x_{id}(t) + v_{id}(t+1)
$$
ここで、それぞれが見つけた最良の位置をパーソナルベスト(pBest)、群全体の最良の位置をグローバルベスト(gBest)と呼びます。
また、$v_{id}$はd次元のi番目の粒子の速度、$x_{id}$はd次元のi番目の粒子の位置、$w$は慣性係数、$c_p$、$c_g$は加速係数と呼ばれる定数、$r_p$、$r_g$は0~1の乱数です。
パラメータである慣性係数にはAIWFを使い、加速係数には一般に多く用いられている2.0の定数を指定しています。
特に慣性係数は結果に大きく影響を与えると言われており、値を大きくするほど大域探索に有効ですが、局所探索には向かないという課題があります。
そこで、AIWFではParticleごとに毎回値を変えることで課題に対応しています。
AIWFにおける慣性係数wは以下の式で求めることができます。
$$
w=
\left\{
\begin{array}{}
\frac{(w_{max} - w_{min})(f-f_{min})}{(f_{avg}-f_{min})}, ( f \leq f_{avg}) \
w_{max}, ( f > f_{avg})
\end{array}
\right.
$$
AIWFのコード
def aiwf(scores, W):
for s in range(SWARM_SIZE):
if scores[s] <= np.mean(scores):
W[s] = (np.min(W) + (((np.max(W) - np.min(W)) * (scores[s] - np.min(scores))) /
(np.mean(scores) - np.min(scores))))
else:
W[s] = np.max(W)
return W
2. 上位1/5のParticleを抽出
CLSを行うParticleを決めるため、PSOの結果Scoreの良かった上位1/5を抽出します。
3. 抽出したParticleに対してCLSを行い、位置を更新
CLSによって局所探索を行います。$x$を各粒子の位置としたとき、CLSは以下の手順で行います。
-
$cx_{i}^{(k)}$を求める
$$
\displaystyle cx_i^{(k)}=
\frac{x_{i}-x_{max,i}}{x_{max,i}-x_{min,i}}
$$ -
$cx_{i}^{(k)}$を基に$cx_{i}^{(k+1)}$を求める
$$
cx_{i}^{(k+1)}=
4cx_{i}^{(k)}(1-4cx_{i}^{(k)})
$$ -
$cx_{i}^{(k+1)}$を基に位置$x_{i}^{(k+1)}$を求め、評価する
$$
x_{i}^{(k+1)}=
x_{min,i}+cx_{i}^{(k+1)}(x_{max,i}-x_{min,i})
$$ -
新しい評価結果が$X^{(0)}=[x_{1}^{0},...,x_{n}^{0}]$より良い場合、または最大反復数に達した場合、結果を出力。それ以外の場合は2.に戻る
CLSのコード
def cls(top_scores, top_positions):
cx, cy = [], []
min_x, min_y = min(top["x"] for top in top_positions), min(top["y"] for top in top_positions)
max_x, max_y = max(top["x"] for top in top_positions), max(top["y"] for top in top_positions)
for i in range(len(top_scores)):
cx.append((top_positions[i]["x"] - min_x) / (max_x - min_x))
cy.append((top_positions[i]["y"] - min_y) / (max_y - min_y))
for i in range(K):
logistic_x = []
logistic_y = []
chaotic_scores = []
chaotic_positions = []
for j in range(len(top_scores)):
logistic_x.append(4 * cx[j] * (1 - cx[j]))
logistic_y.append(4 * cy[j] * (1 - cy[j]))
# 位置の更新
chaotic_x, chaotic_y = chaotic_update_position(logistic_x[j], logistic_y[j], min_x, min_y, max_x, max_y)
chaotic_positions.append({"x": chaotic_x, "y": chaotic_y})
# score評価
chaotic_scores.append(evaluation(chaotic_x, chaotic_y))
# 新しいscoreが前より優れていれば値を返し,それ以外はcx, cyを更新して繰り返す
if min(chaotic_scores) < min(top_scores):
print("Better Chaotic Particle found")
return chaotic_scores, chaotic_positions
cx = logistic_x
cy = logistic_y
return chaotic_scores, chaotic_positions
# Chaotic position更新
def chaotic_update_position(x, y, min_x, min_y, max_x, max_y):
new_x = min_x + x * (max_x - min_x)
new_y = min_y + y * (max_y - min_y)
return new_x, new_y
4. CLSを行ったParticleの位置情報を基に探索範囲を削減
CLSの結果を基に次の探索範囲を削減します。
CLSを用いたParticleの位置情報を基に、以下の式を用いて探索範囲を再指定します。
ただし、論文の通り実装したとき、最小値に対して複数の最小値の中の最大値を用い、最大値に対して複数の最小値の中の最小値を用いると、最小値と最大値が逆転してしまったため、実装では最小値には最小値、最大値には最大値を用いて探索範囲を広く取りました。
探索範囲削減のコード
def search_space_reduction(top_positions):
min_x, min_y, max_x, max_y = [], [], [], []
min_x.append(min(top["x"] for top in top_positions))
min_y.append(min(top["y"] for top in top_positions))
max_x.append(max(top["x"] for top in top_positions))
max_y.append(max(top["y"] for top in top_positions))
x = [top.get("x") for top in top_positions]
y = [top.get("y") for top in top_positions]
for i in range(len(top_positions)):
min_x.append(x[i] - R * (max_x[0] - min_x[0]))
min_y.append(y[i] - R * (max_y[0] - min_y[0]))
max_x.append(x[i] + R * (max_x[0] - min_x[0]))
max_y.append(y[i] + R * (max_y[0] - min_y[0]))
# 論文通り new_min_x = max(min_x) などにすると最小値と最大値が逆転してしまうので,修正
new_min_x, new_min_y = min(min_x), min(min_y)
new_max_x, new_max_y = max(max_x), max(max_y)
search_space_x = {"min": new_min_x, "max": new_max_x}
search_space_y = {"min": new_min_y, "max": new_max_y}
return search_space_x, search_space_y
5. 新しい探索範囲内で下位4/5のParticleをランダムに再生成
削減した新しい探索範囲内には下位4/5のParticleが入らないので、範囲内に収まるように新しく生成します。
Particleの生成に関しては初期設定と同様ランダムに生成しています。
6. 各Particleの評価を行い、停止条件を満たしていれば終了、満たしていなければ1.に戻る
各Particleに対して評価を行います。
この時、事前に閾値として設定したScoreより良かった場合、または最大探索回数に達した場合は探索を終了し、結果を出力します。
条件を満たしていない場合は1.に戻り、またPSOから実行して探索を継続します。
ベンチマーク関数での評価結果
最適化アルゴリズムを評価するための関数として、多くのベンチマーク関数が存在します。
ベンチマーク関数が詳しく紹介されているものとしてtomitomi3さんの記事があります。
今回はこの中でも紹介されているSphere functionを用いました.この関数の最適解は$f_{min}(0,...,0)=0$となっています。
今回はScore < 1.000e-15または反復回数10回を終了条件としました。
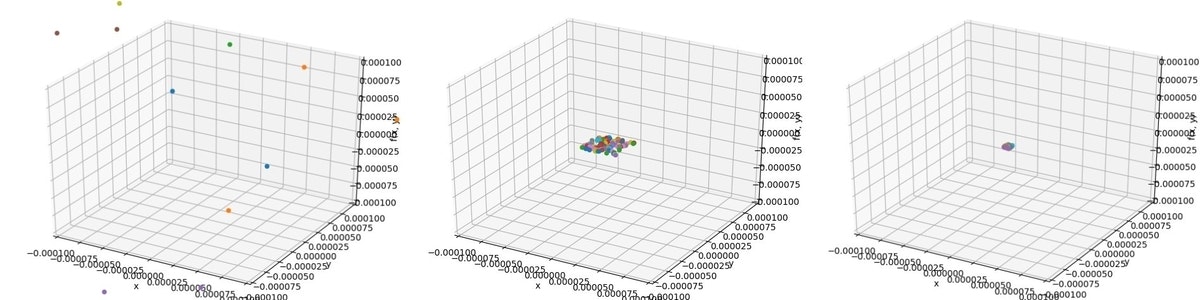
結果として、図のように収束していく様子が観測できました。
また、画像の描画無しで実行した場合及びシンプルなPSOを実行した場合の結果は以下のようになりました。
CLSによって精度が向上した場合はScoreも更新され、精度が向上しなかった場合はCLS前のScoreが引き継がれています。
探索範囲は毎回削減され、Scoreも向上していることが確認できます。
また、下のPSOのみを実行した結果と比較すると、精度が向上している反面,時間が掛かっていることが分かります。
CPSO log and result
Lap: 1
CLS:
before: 1.856166459555566e-09
after: 1.7476630375799616e-07
Search Area:
before
x: {'min': -5.0, 'max': 5.0}
y: {'min': -5.0, 'max': 5.0}
after
x: {'min': -0.0010838869646188037, 'max': 0.0013954791030881871}
y: {'min': -0.001201690486501598, 'max': 0.0016078160576153975}
Score: 1.856166459555566e-09
Lap: 2
CLS:
before: 2.0926627088682597e-13
Better Chaotic Particle found
after: 7.821496571701076e-14
Search Area:
before
x: {'min': -0.0010838869646188037, 'max': 0.0013954791030881871}
y: {'min': -0.001201690486501598, 'max': 0.0016078160576153975}
after
x: {'min': -7.880347663659637e-06, 'max': 1.5561134225910913e-05}
y: {'min': -1.83517959693168e-05, 'max': 1.853229861175588e-05}
Score: 7.821496571701076e-14
Lap: 3
CLS:
before: 6.562680339774457e-17
Better Chaotic Particle found
after: 5.0984844476716916e-17
Search Area:
before
x: {'min': -7.880347663659637e-06, 'max': 1.5561134225910913e-05}
y: {'min': -1.83517959693168e-05, 'max': 1.853229861175588e-05}
after
x: {'min': -3.794413350751951e-07, 'max': 1.6057623588141383e-07}
y: {'min': -2.7039514283878003e-07, 'max': 8.373690854089289e-08}
Score: 5.0984844476716916e-17
Best Position: {'x': 6.92085226884776e-09, 'y': 1.7568859807915068e-09}
Score: 5.0984844476716916e-17
time: 0.7126889228820801
PSO result
Best Position: {'x': -0.23085945825227583, 'y': -0.13733679597570791}
Score: 4.218973135139706e-06
time: 0.006306886672973633
まとめ
今回実験してみて,CPSOの精度のと実行時間について知ることができました.今回は最適解が一つ(単峰性)のシンプルな関数で評価しましたが,多峰性の関数などで評価した場合などについても機会があれば調べたいと思います.