第3章に引き続き、深層学習(青イルカ本)の第4章を読み進めていきます.
本投稿(連載)を一緒に読めば事前知識なしでも読み進められる...といったものを目指しています.
本章の概要
本章では,勾配降下法に必要な勾配$\nabla E$を計算する誤差逆伝播法(Backpropagation, BP法)を扱います.
誤差逆伝播法の一般式を直ちに導くのは難しいため,3つのステップを踏んでいます.
最初の2ステップでは,表記の簡素化のためにバイアスを常に1である重みとして考えて扱います(こうすると都合が良いのです).
- 4.2節では2層ネットワークのみを扱い,勾配を計算するヒントを掴みます.
- 4.3節では4.2節の内容を多層ネットワークへ拡張します.
- 4.4節ではバイアスと共に,行列表現をすることでミニバッチを考慮に入れます.
最後に,4.5節では本手法の問題点である勾配消失問題について触れて,次章に話しを繋げます.
要点
誤差逆伝播法を用いると,勾配降下法に用いる誤差勾配$\frac{\partial En}{\partial w_{ji}^{(l)}}$の計算を簡単にすることができます.
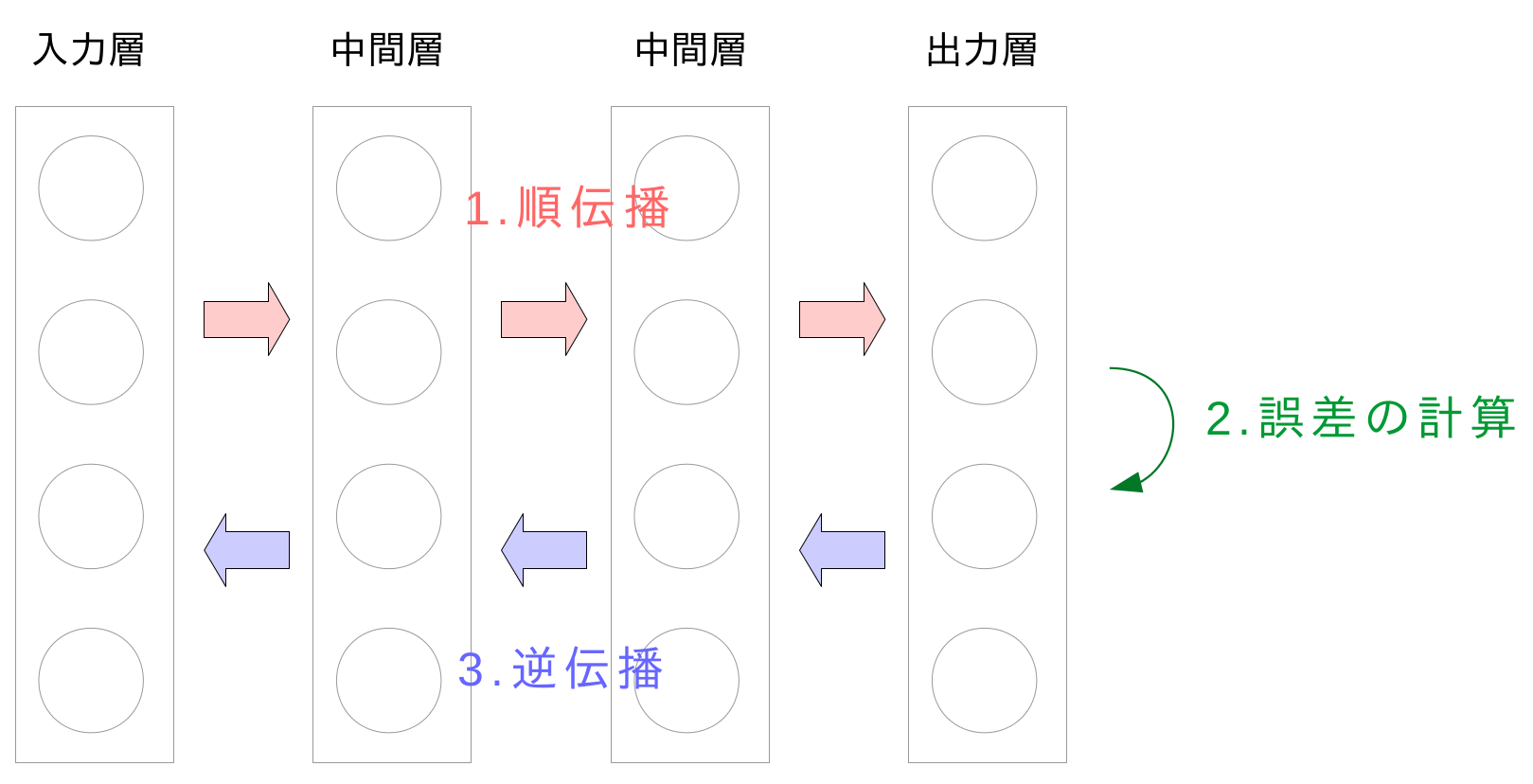
結論から言えば$\frac{\partial En}{\partial w_{ji}^{(l)}} = \delta_{j}^{(l)}z_{i}^{(l-1)}$と表すことができます.ここで$\delta_{j}^{(l)}$は各層の各ユニットの誤差に関する数値で,次の図に示す3ステップで計算します.$z_{i}^{(l-1)}$は順伝播の過程で求まりますから,これで$\frac{\partial En}{\partial w_{ji}^{(l)}}$が計算できます.
以下にその導出の詳細を追っていきます.
本文詳細
大まかな流れがわかったところで,本文に沿って読み進めていきます.
4.2 2層ネットワークの計算
本節の目的は,試しに2層ネットワークで勾配の計算をしてみることです.
2層ネットワークにおいて,重みは出力層の$w_{ji}^{(3)}$と中間層の$w_{ji}^{(2)}$ですので,求める勾配は対応する$\frac{\partial E_n}{\partial w_{ji}^{(3)}}$と$\frac{\partial E_n}{\partial w_{ji}^{(2)}}$であることを意識しておきましょう.
本題に入る前に,添字について確認しておきます.
$w_{ji}^{(l)}$は$(l-1)$層の$i$層から$l$層の$j$番目のユニットへの重みのことです.これを第$l$層の重みと表現する点も注意しておきましょう.
出力層の重みの勾配
まずは出力層の重みの勾配$\frac{\partial E_n}{\partial w_{ji}^{(3)}}$を求めます.
yの微分について補足
右辺の$\boldsymbol{y} / {\partial w_{ji}^{(3)}}$はベクトルですが,式(4.3)よりその$j$成分のみが$z_{i}^{(2)}$で,それ以外の成分は$0$,つまり $ \frac{\partial \boldsymbol{y}}{\partial w_{ji}^{(3)}} = (0 \ ... \ 0 \ z_{i}^{(2)} \ 0 \ ... \ 0)^{\top} $ の形となります.
この手の計算は,後に何度となく出てきますので,導出過程を一応書いておきます.
なお$I, J$を添字$i, j$の最大値(その層でのユニット数)としました.
\begin{align}
\boldsymbol{y} &= (y_1\,...\,y_j\,...\,y_J)^{\top}\\
\frac{\partial \boldsymbol{y}}{\partial w_{ji}^{(3)}} &= (0\,...\,0\,\frac{\partial y_j}{\partial w_{ji}} \,0\,...\,0)^{\top}\\
\end{align}
次に$y_{j}$の微分は次のようになります.
\begin{align}
\frac{\partial y_j}{\partial w_{ji}^{(3)}} &= \frac{\partial}{\partial w_{ji}^{(3)}} \sum_{i} w_{ji}^{(3)}z_i^{(2)}\\
&= \frac{\partial}{\partial w_{ji}^{(3)}} ( w_{j1}^{(3)}z_i^{(2)} + ... + w_{ji}^{(3)}z_i^{(2)} + ... + w_{jI}^{(3)}z_i^{(2)} )\\
&= 0 + ... + 0 + z_i^{(2)} + 0 + ... + 0 = z_i^{(2)}
\end{align}
以上より$ \frac{\partial \boldsymbol{y}}{\partial w_{ji}^{(3)}} = (0 \ ... \ 0 \ z_{i}^{(2)} \ 0 \ ... \ 0)^{\top} $が求まりました.
中間層の重みの勾配
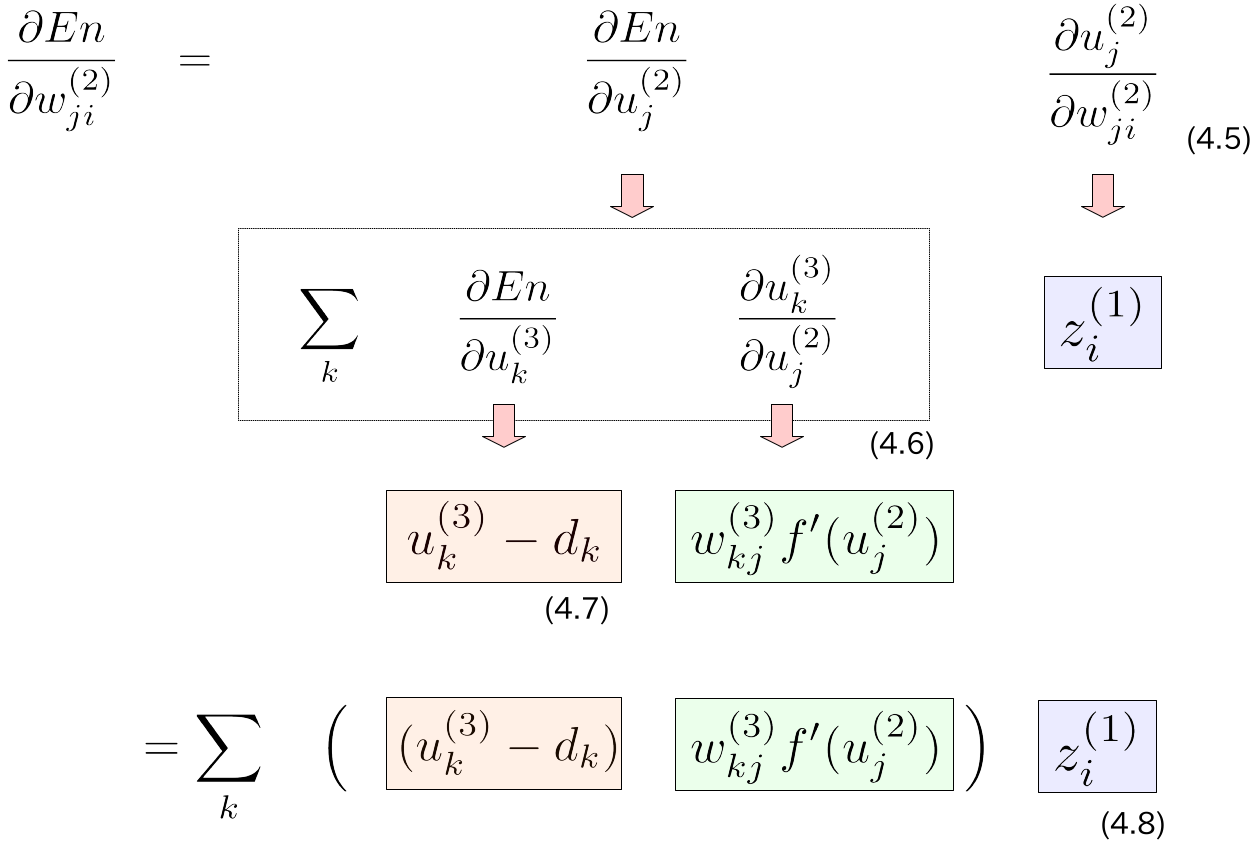
続いて中間層の重みの勾配$\frac{\partial E_n}{\partial w_{ji}^{(2)}}$を求めます.導出の流れをまとめておきます.
式(4.6)で$\sum$が出てきているのは,$\frac {\partial En} {\partial u_{j}^{(2)}}$が多変数関数の偏微分であるためです(参考: 多変数関数の合成関数の微分(高校数学の美しい物語)).
以上の計算から,2層ネットワークの勾配計算を行うことができました.
4.3 多層ネットワークへの一般化
本節では,4.2節で導いた勾配計算を,多層ネットワークへ一般化します.
さて,任意の勾配$ \frac{\partial E_n}{\partial w_{ji}^{(l)}}$について,4.2節で導いた式(4.8)が適用できそうにも見えますが,実はそうもいきません.式(4.6)に現れる$\frac{\partial E_n}{\partial u_{k}^{(l+1)}}$は式(4.7)のようには計算できないためです.この部分は仕方ないので,式(4.6)を$l$層の式に置き換えて,漸化式による解決を図ります.
\frac {\partial En} {\partial u_{j}^{(l)}} = \sum_{k} \left( \frac{\partial En}{\partial u_{k}^{(l+1)}} \ w_{kj}^{(l+1)}f'(u_{j}^{(l)}) \right)
ここで,$w_{kj}^{(l+1)}$は入力データとして既に存在し,$f'(u_{j}^{(l)})$は順伝播が計算されていれば得られることに注意してください.
これにより,順伝播が計算されていれば,$\frac{\partial En}{\partial u_{k}^{(l+1)}}$, $\frac{\partial En}{\partial u_{k}^{(l)}}$, ...と逆順に計算でき,無事解決できます.
これで準備は整いました.上図の式(4.8)を式(4.7)の部分を計算せずに$l$層の式に置き換えると,次のようになります.
\frac {\partial En} {\partial w_{ji}^{(l)}} = \sum_{k} \left( \frac{\partial En}{\partial u_{k}^{(l+1)}} \ w_{kj}^{(l+1)}f'(u_{j}^{(l)}) \right) z_{i}^{(l-1)}
いま,$\frac{\partial En}{\partial u_{k}^{(l+1)}}$を漸化式によって得ることができ,$z_{i}^{(l-1)}$は順伝播を計算されていれば得られるので,これで$\frac {\partial En} {\partial w_{ji}^{(l)}}$を計算することができます.
以上をまとめると,次のステップを踏めば良いことが分かります.これが誤差伝播法なのです.
1. 順伝播を先に計算しておく.
2. 出力と正解値の差$u_k^{(l)} - d$を計算する.
3. 出力層から逆順に$\frac{\partial En}{\partial u_{k}^{(l)}}$を計算する.
4. $\frac {\partial En} {\partial w_{ji}^{(l)}}$を計算する.
4.4 勾配降下法の完全アルゴリズム
出力層のデルタ
本項では,回帰,二値分類,多クラス分類のいずれにおいても,出力層$L$のユニット$j$のデルタ$\delta_{j}^{(L)}$がネットワークの出力$y_j$とその目標出力$d_j$の差になることを見ます.
本稿では多クラス分類の場合についてのみ途中式を補足説明します.
まず交差エントロピーは次式でした.
E_n = -\sum_{k} d_k \log y_k = -\sum_{k} d_k \log \left( \frac{ \exp(u_{k}^{(L)}) }{ \sum_{i}\exp(u_{i}^{(L)})} \right)
ここで,この関数を$\partial u_{j}^{(L)}$で微分することを考えると,$k = j$の時に微分対象の変数となる(定数でない).
一方で$i$についてはソフトマックス関数の性質から必ず$u_j$が出現することに注意する.
\frac{\partial E_n}{\partial{u_j^{(L)}}} = - \sum_{k} d_k \frac{1}{y_k} \frac{\partial y_k}{\partial{u_j^{(L)}}} \\
$k = j$のとき
\begin{eqnarray}
\frac{\partial y_k}{\partial {u_j^{(L)}}} &=& \frac{\exp{(u_j^{(L)})} \sum_i {\exp{(u_i^{(L)})}} - \exp{(u_j^{(L)})}\exp{(u_j^{(L)})}} {\left(\sum_i{\exp{(u_i^{(L)})}}\right)^2} \\
&=& y_j - y_{j^2}
\end{eqnarray}
$k\neq j$のとき
\begin{eqnarray}
\frac{\partial y_k}{\partial {u_j^{(L)}}} &=& \frac{-\exp{(u_k^{(L)})}\exp{(u_j^{(L)})}}{\left(\sum_i{\exp{(u_i^{(L)})}}\right)^2} \\
&=& -y_{k} y_{j}
\end{eqnarray}
以上から
\begin{eqnarray}
\frac{\partial{y_k}}{\partial{u_j^{(L)}}} &=& - d_j \frac{1}{y_j} (y_j - y_{j^2}) - \sum_{k \neq j} d_k \frac{1}{y_k} (-y_{k} y_{j}) \\ &=& y_j - d_j
\end{eqnarray}
勾配計算の差分近似計算
ここでは,検算のために勾配を近似して計算する方法について述べられています.
機械学習の差分についてのみではなく,コンピュータで微分を計算する上でよく用いられる一般的な方法です.微分の定義を思い出すと,$f'(x) = \lim_{h \to 0} \frac{f(x + h)}{h}$でした.コンピュータ上で微分値を得るには$0$に近い$h$が欲しい訳ですが,このような時に十分小さな値として用いられるのが$\epsilon$です.ちなみにプログラム言語だとC言語ではfloat.hに,pythonではsysやnumpyに定義されています.
4.5 勾配消失問題
逆伝播法は式(4.13)のように線形な計算なので,層が深くなるほど発散しやすい(0に収束していまう)という性質があります.
これに対応するための方法に,5章で扱う自己符号器による事前学習があります.
補足事項
wikipediaから本書に記載のない事項を抜粋します.
テクニック
バッチ学習よりも確率的勾配降下法によるオンライン学習を使う
オンライン学習において訓練データが一周したら毎回シャッフルし直す
入力は、平均を0にし、主成分分析により線形相関を取り除き、分散が1になるように線形変換する。面倒だったら主成分分析は省略しても良い。
活性化関数は原点を通る物を使用する。標準シグモイド関数は$f(0) = 0.5$のため不適切で、$tanh$は原点を通るので良い。Yann LeCunらは $1.7159 * tanh(2 / 3 * x)$を薦めているが、Xavier Glorotらは単に$tanh(x)$で十分としている。Yann LeCun らの意図は$f(±1) = ±1$にすることにある。どちらも $f(0) = 0, f'(0) = 1$。
限界
勾配が0に近い部分が存在する活性化関数を使っていると勾配消失を起こしやすい。
さて,次は第5章 自己符号化器です.引き続き友人(y_ujitoko)が易しく丁寧に解説してくれるはずです.