雑なアルゴリズムと最新のCPUはどちらが速いのか？

この記事は NSSOL Advent Calendar 2021 その2 、12日目の記事です。
今年は順調に埋まってたしエントリーしなくていいかなーと思ってたらその2ができてたので急遽エントリーしました。

先日PCがぶっ壊れまして

「順当に埋まってたから今年はエントリーしなくていい」なんてことも書きましたが、それも理由の一部ではありながらも、実は最大の理由は「 PCがぶっ壊れたから 」でした。
1か月と少し前の10月30日、なんとなくWebブラウジングしていたら突然PCの電源が落ち、7年をともにした愛しのPCがそのまま帰らぬ人となってしましました。

元々Windows 11不適合だったこともあり、そのうち買い替えだとは思っていたんですが、少しそれが早まった格好です。
10月30日から見て1週間後には最新の第12世代 Intel CPU、Alder Lakeが登場しようとしていたので、これはもう決めねばならないと思って新PCを準備していました。

とはいえ、発売直後の品薄、そしてDDR5メモリの品薄も相まって、手元にくるのはずいぶん後だろうと思っていたので今年のAdvent Calendarは眺めていようと思ったわけです。

しかし新しいPCが誕生しました

そう思っていたところ、ついに新しいPCが誕生しました。主なスペックは以下の通りです。

• CPU
  • Intel Core i7 12700K (12Core/20Thread)
• MEM
  • DDR5-4800 32GB
• SSD
  • M.2 NVMe 1TB
• GPU
  • GeForce 1660 SUPER 6GB
• OS
  • Windows 11 Pro

今のところデジカメ現像に使っているLightroomの操作が軽快になったことは体感できていますが、いまひとつこいつの実力がわかりません。
というわけで何か、何かわかりやすいレースのようなものでこいつの実力を測りたくなってきました。

そうだ、円周率を計算しよう

コンピュータの計算能力を測るとき、皆さんは何をやらせますか？
そうですね、円周率の計算です。そうではなくて自然対数の底、ネイピア数を思い浮かべた人はぜひ仲良くしてください。

というわけで、今回はいくつかのアプローチで 雑に 円周率を計算しつつ、眠っていた古いPCとのスピードを比較することで、新しいPC・新しいCPUの実力を知っていきたいと思います。

比較対象にする古いPC

比較対象とする古いPCはこちらです。

• CPU
  • Intel Core i5 4210M (2Core/4Thread)
• MEM
  • DDR3L-1600 8GB
• SSD
  • SATA SSD 256GB
• GPU
  • OnBoard (Intel HD Graphics 4600)
• OS
  • Windows 10 Pro

本当の本当にブラウジングするだけならまだなんとか...って感じではありますが、メモリリッチな最近のブラウザでは物足りなさがあります。

円周率の求め方

円周率の求め方は多種多様です。高校レベルでも考え付くものから、発想が難しいだけで計算は単純なものなど様々です。
今回はそのうち、手元で簡単に実装可能なものとして、以下3通り、そして円周率計算の世界記録をたたき出す高効率アルゴリズムを加えて4通りで計算します。

• 正多角形
• ゼータ関数(2)
• モンテカルロ法
• Chudnovskyの公式

それでは、順に計算してみましょう。

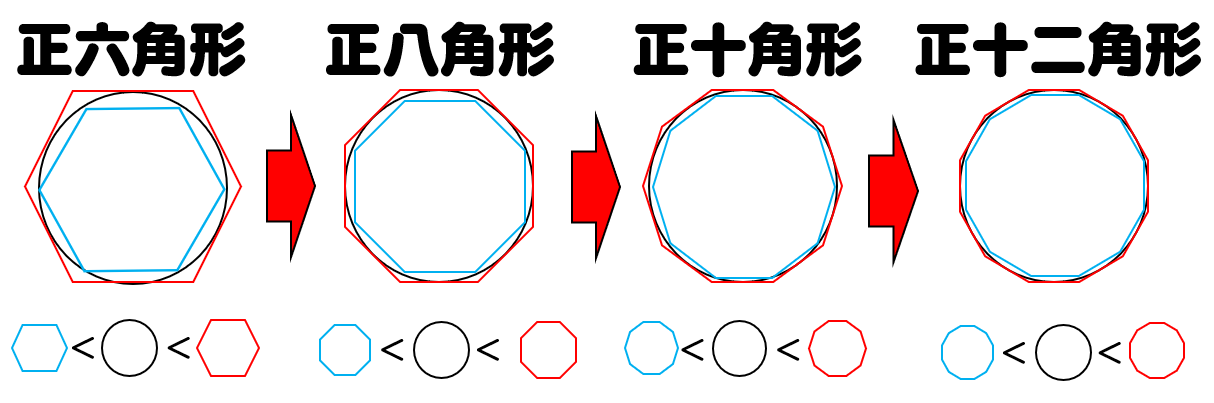
正多角形

ではまず最初は、正多角形を使った近似を考えていきます。
このアプローチはいつぞやの東大入試において「円周率が3.05より大きいことを示せ」という問題の解答例としても有名です。

発想としては単純で、

引用: **[円周の公式｜なぜ直径×円周率で計算できるのか＆円周率を調べる方法（小学校算数のわかりやすい教え方）](https://sugaku.fun/circumference/)**

というように、円に内接/外接する正多角形の周長は常に

（内接正多角形の周長） < （円周） < （外接正多角形の周長）

となりますから、 正∞角形 = 円周 と考えることができ、これを円周率計算に利用することができます。

計算方法

というわけでPythonで書いたコードがこちら。コードで見るとぱっと見よくわかりませんが、高校で習った 余弦定理 を使っています。

RegularPolygonApprox.py

import sys
import numpy as np

count = int(sys.argv[1])

rad = np.radians(360 / count)
calc_pi = count * np.sqrt(2 - 2 * np.cos(rad)) / 2

print("RegularPolygonApprox(" + "{:,}".format(count) + ") = " + str(calc_pi))

NumPyを使うとcosやsqrtが普通に扱えるのでこれを使います。 インチキ 便利ですね。
実行してみると、

実行結果

$ python3 RegularPolygonApprox.py 100
RegularPolygonApprox(100) = 3.141075907812832

となります。正100角形で円周率3.141まで迫ります。しかしまだまだですね。

精度を上げると？

この方法の場合、引数に与えている数字を大きくすれば導かれる円周率の精度が上がっていきます。
どれくらい近いのかを分かりやすく見るべく、計算コードのあとに精度チェッカーをつけてみましょう。

RegularPolygonApprox.py（精度チェッカー付き）

import sys
import numpy as np

count = int(sys.argv[1])

rad = np.radians(360 / count)
calc_pi = count * np.sqrt(2 - 2 * np.cos(rad)) / 2

print("RegularPolygonApprox(" + "{:,}".format(count) + ") = " + str(calc_pi))

# 精度確認用に正しい円周率を取得
pi = np.pi

# 差をとって常用対数で精度を評価（マイナスがでかいほど近い）
print("RegularPolygonAccuracy(" + "{:,}".format(count) + ") = " + str(np.log10(np.abs(pi - calc_pi))))

とすると、

実行結果

$ python3 RegularPolygonApprox.py 100
RegularPolygonApprox(100) = 3.141075907812832
RegularPolygonAccuracy(100) = -3.2867230639022544

という感じになります。 3.141 という小数点以下3桁まであっているので -3 ちょっとの値が出ます。
ここで正1000角形を使ってみるとより円周率に近づきますが、

実行結果

$ python3 RegularPolygonApprox.py 1000
RegularPolygonApprox(1,000) = 3.1415874858807182
RegularPolygonAccuracy(1,000) = -5.286701943683555

となり、精度が上がっていることがよく分かるようになりました。

ゼータ関数(2)

次はゼータ関数の特殊値を用いた方法です。こちらの数式をご覧ください。

ζ(2) = \frac{1}{1^2} +\frac{1}{2^2} +\frac{1}{3^2} +\frac{1}{4^2} +\cdots= \frac{\pi^2}{6}

知らない人にはなんのこっちゃというような等式ですが、とにかくこういう関係が成り立つと知られています。一般にはゼータ関数と呼ばれる形ですが、この2乗の分母を持つ形を特にバーゼル問題と呼んだりします。

計算方法

それではいってみましょう。最後にルートをとりますが、基本的な計算としては割と単純です。

Zeta2Approx.py

import sys
import numpy as np

count = int(sys.argv[1])
zeta2 = 0

for num in range(1,count):
    zeta2 += 1/(num ** 2)

calc_pi = np.sqrt(6 * zeta2)

print("Zeta2Approx(" + "{:,}".format(count) + ") = " + str(calc_pi))

実行してみます。

実行結果

$ python3 Zeta2Approx.py 100
Zeta2Approx(100) = 3.1319807472443624
Zeta2Accuracy(100) = -2.0171904694391722

難しそうな形をしている割に3.13までしかいきませんでした。残念ですね。

モンテカルロ法

続いては 乱数を使った運ゲー式の有名な円周率計算 です。

考え方はこれまた以下に引用する画像がすべてですが、ある正方形の領域があり、その領域内の1点をランダムにとることを考えます。
そしてその点が正方形に内接する円に入っているなら内側カウント+1（青色の点）、外側だったらノーカウント（赤色の点）というように、テキトーに点を取り、円の内外で個数をカウントしていきます。

引用: **[もう円周率で悩まない！πの求め方10選](https://www.procrasist.com/entry/pi_1)**

左側の100個程度ではよくわかりませんが、右側の10000個になるとはっきりと円の形が見えてきます。
このとき、円の半径が1だとすると青の円の面積はちょうどπになり、正方形は円の直径2が1辺にあたるので赤を含めた面積が2×2で4になります。
つまり、この点をカウントする操作を繰り返していくと、

\frac{\pi}{4} \fallingdotseq \frac{（青い点の個数）}{（点の個数）}

になるはずだということがわかります。これを利用するのがモンテカルロ法です。よく思いつくもんですね。

計算方法

モンテカルロ法による計算をコード化するとこうなります。乱数(x,y)をとって2乗の足し算が1以下かどうか見るのがポイントですね。

MontecarloApprox.py

import sys
import numpy as np
import random

count = int(sys.argv[1])
inside_circle = 0

for num in range(count):
    x = random.uniform(-1, 1)
    y = random.uniform(-1, 1)

    if x ** 2 + y ** 2 <= 1:
        inside_circle += 1

calc_pi = ( inside_circle / count ) * 4

print("MontecarloApprox(" + "{:,}".format(count) + ") = " + str(calc_pi))

まぁ、計算上の本質は乱数を生成するところにあるんですがそこはPythonのライブラリに頼ります...。
では実行してみましょう。

$ python3 MontecarloApprox.py 100
MontecarloApprox(100) = 3.12
MontecarloAccuracy(100) = -1.6656939825574797

うーん、これはなかなかひどいですね。まぁ100個しか使ってないので当然です。
そして、このモンテカルロ法は乱数を使っているので、実行するごとに数値が変わります。

 python3 MontecarloApprox.py 100
MontecarloApprox(100) = 2.88
MontecarloAccuracy(100) = -0.5823744566406384

$ python3 MontecarloApprox.py 100
MontecarloApprox(100) = 2.96
MontecarloAccuracy(100) = -0.7409017250327223

$ python3 MontecarloApprox.py 100
MontecarloApprox(100) = 3.48
MontecarloAccuracy(100) = -0.47056021752786215

どうやら最初の3.12は相当優秀な結果だったようです。試しに10000まで増やしてみると...

$ python3 MontecarloApprox.py 10000
MontecarloApprox(10,000) = 3.1416
MontecarloAccuracy(10,000) = -5.133924825297861

$ python3 MontecarloApprox.py 10000
MontecarloApprox(10,000) = 3.1424
MontecarloAccuracy(10,000) = -3.0929400814353767

$ python3 MontecarloApprox.py 10000
MontecarloApprox(10,000) = 3.1448
MontecarloAccuracy(10,000) = -2.493854131460185

だいぶマシになりました。

参考：Chudnovskyの公式

最後に、さらによくわからない計算方法です。

\frac{1}{\pi} = 12 \sum_{n=0}^\infty \frac{(-1)^n (6n)! (545140134 n + 13591409)}{(3n)!(n!)^3 640320^{3n + 3/2}}

さっぱりわかりませんがとにかくこれで円周率が計算できるようです。なんでも、nを1上げるだけで桁数が14桁上がるとか。

計算方法

コードはこちら...と言いたいところですが、さすがにこれは先人のものをお借りすることにします。

1億桁の出力にも対応する手前、ファイル書き出しになっていましたが、他の計算方法にあわせて少し出力だけ手直ししました。（コード自体は割愛）

実行結果

$ python3 ChudnovskyApprox.py 100
ChudnovskyApprox(100) = 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480864
ChudnovskyAccuracy(100) = -100.08540254879130698707314373776576277920423602833644262890077715745944788464831321467805937693692672883911646

ここの引数100は「100サイクル計算せよ」ではなく、「100桁まで出力せよ」なので精度チェックがきれいに-100までいっています。
ここの計算では検算するための検算するための円周率を100桁までしか用意していないので、これがカンストですね。

桁数を指定しているので、

実行結果その2

$ python3 ChudnovskyApprox.py 10
ChudnovskyApprox(10) = 3.1415926535897932384
ChudnovskyAccuracy(10) = -19.203124794693094187

$ python3 ChudnovskyApprox.py 30
ChudnovskyApprox(30) = 3.141592653589793238462643383279502884199
ChudnovskyAccuracy(30) = -38.73740639372307672082943901594678185445

$ python3 ChudnovskyApprox.py 50
ChudnovskyApprox(50) = 3.14159265358979323846264338327950288419716939937510582097496
ChudnovskyAccuracy(50) = -58.8122624065112103751305576198125583007538058570419987896880

という感じで順調に精度があがっていきます。
なお、指定より実際の精度がいいのは指定桁まで正しい値を出すべく、内部的にはもう少し深いところで計算しているためですね。

計算時間と精度の比較

それでは、ここまで作ってきた各計算方法を使って、どれくらいの時間でどれくらいの精度が得られるのかチェックしてみます。
時間の計測は単純にtimeコマンドを使います。

実行時間の計測

$ time python3 RegularPolygonApprox.py 100
RegularPolygonApprox(100) = 3.141075907812832
RegularPolygonAccuracy(100) = -3.2867230639022544

real    0m0.066s
user    0m0.134s
sys     0m0.326s

としたときの user を何も考えずに処理時間だとします。
では、CPUごとにまとめて処理時間を見てみましょう。

計算方法	N	精度	Core i7 12700K	Core i5 4210M	差	向上率
正多角形	100	-3.29	0.164	0.286	-0.122	42.66%
正多角形	1,000	-5.29	0.14	0.335	-0.195	58.21%
正多角形	10,000	-7.29	0.21	0.484	-0.274	56.61%
正多角形	100,000	-7.55	0.115	0.268	-0.153	57.09%
正多角形	1,000,000	-6.93	0.154	0.29	-0.136	46.90%
ゼータ関数(2)	100	-2.02	0.155	0.319	-0.164	51.41%
ゼータ関数(2)	1,000	-3.02	0.25	0.272	-0.022	8.09%
ゼータ関数(2)	10,000	-4.02	0.211	0.287	-0.076	26.48%
ゼータ関数(2)	100,000	-5.02	0.163	0.346	-0.183	52.89%
ゼータ関数(2)	1,000,000	-6.02	0.322	0.646	-0.324	50.15%
モンテカルロ法	100	-1.21	0.163	0.312	-0.149	47.76%
モンテカルロ法	1,000	-1.13	0.16	0.249	-0.089	35.74%
モンテカルロ法	10,000	-1.72	0.137	0.285	-0.148	51.93%
モンテカルロ法	100,000	-2.36	0.25	0.371	-0.121	32.61%
モンテカルロ法	1,000,000	-2.74	0.567	1.176	-0.609	51.79%
参考：Chudnovsky	10	-19.20	0.25	0.279	-0.029	10.39%
参考：Chudnovsky	50	-58.81	0.173	0.347	-0.174	50.14%
参考：Chudnovsky	100	-100.09	0.225	0.259	-0.034	13.13%

という結果になりました。うーむ。
当たり前の話として新しいPC側、Core i7 12700Kのほうが速い傾向です。が、全体的にどれも1秒を切る水準なので、性能差がわかるような...わからんような...。

それぞれ振り返ってみましょう。

正多角形

これは明らかに結果がおかしいです。正N角形のNをどんどん大きくしていくわけですから、それによって導かれる円周率は真の値に近づき続けるはずです。
が、結果を見てみると

計算方法	N	精度	Core i7 12700K	Core i5 4210M	差	向上率
正多角形	100	-3.29	0.164	0.286	-0.122	42.66%
正多角形	1,000	-5.29	0.14	0.335	-0.195	58.21%
正多角形	10,000	-7.29	0.21	0.484	-0.274	56.61%
正多角形	100,000	-7.55	0.115	0.268	-0.153	57.09%
正多角形	1,000,000	-6.93	0.154	0.29	-0.136	46.90%

というように、正10万角形の結果と正100万角形の結果で精度が落ちています。おそらく、詳しくはみていませんが、

RegularPolygonApprox.py（抜粋）

rad = np.radians(360 / count)
calc_pi = count * np.sqrt(2 - 2 * np.cos(rad)) / 2

のところで、radが小さくなりすぎたときに、cosやsqrtを扱うNumPyの精度が追い付かなくなっているのでしょう。
今回実装した...といっても実態はNumPyの関数に頼り切りだったので、ここの壁にぶつかってしまった格好です。

ゼータ関数(2)

こちらも計算的にはNumPyのsqrtに頼っていますが、100万までの値では明らかにおかしいといった結果にはなっていないようです。
Nを10倍にするごとに精度が1上がっていく感じに見え、100万以上のNについてもその傾向は維持されていましたが、こちらもどうやら1億で頭打ちのようです。

計算方法	N	精度	Core i7 12700K
ゼータ関数(2)	100万	-6.02	0.322
ゼータ関数(2)	1000万	-7.02	1.509
ゼータ関数(2)	1億	-8.07	14.721
ゼータ関数(2)	10億	-8.07	190.044

特段変数の型や桁数を気にしたわけではなかったので、8桁で限界なんでしょう。

モンテカルロ法

モンテカルロ法は今回扱った方法の中で、最も計算効率が悪く、そして信頼性の低い方法でした。
100万回の試行で3.14くらいを出すのが精いっぱいで、それ以上は回数を増やしてもほとんど精度は向上しませんでした。

計算方法	N	精度	Core i7 12700K
モンテカルロ法	100万	-3.21	0.465
モンテカルロ法	1000万	-3.11	3.201
モンテカルロ法	1億	-3.78	30.71
モンテカルロ法	10億	-4.55	306.057

こちらも乱数生成の根幹をライブラリに委ねているので、ここからどこまで精度を高められるかはrandomメソッドの実装次第ですね。

Chubnovskyの公式

まぁ、やる前からわかってはいましたが、このChubnovskyの公式が圧倒的な速度・信頼性をもっていました。
他の方法でいくらNを上げても10桁以上の精度を得られることはありませんでしたが、この方法は本当に難なく100桁をクリアしています。

せっかくなので元記事にもある通り、僕の環境でも 1億桁の計算 にチャレンジしてみます。あちらはCore i5 8400だったそうですが、どうなるでしょうか。

計算方法	精度	Core i7 12700K	Core i5 4210M	参考：Core i5 8400
Chudnovsky	1億桁	347.789	751.311	644

ここまでのスケールになるとさすがにCPUの差が如実に表れてきます。
タスクスケジューラを見る限りは、シングルスレッドでしか動いていないようでしたが、それでも2倍近い差がついていますね。

おわりに

今回は新しいPCが手に入ったからとなんとも雑な計算を繰り広げてみました。
当初の目論見としては「 いくら計算リソースが潤沢になったといっても、速さも正確さも研ぎ澄まされたアルゴリズムには敵わないよね。アルゴリズム大事だよね。 」って話をしたかったんですが、CPUが強くなるのとは次元の違う差だったので、やや当初のイメージとは違う読み味になりました。
このことから、アルゴリズム界では「レベルを上げて物理で殴る」なんてことはさっぱり通用しないことがよくわかります笑

ちなみに、現在の円周率計算の世界記録は、今回紹介したChudnovskyの公式を用いてマルチスレッドで処理できるようにした y-cruncher というソフトを使って計算されたもののようです。

2021年8月の記録ですが、62.8兆桁の計算に108日間かかったとのこと。しかしまだ非公式扱いらしく、

ちなみに、62.8兆桁まで計算されたという円周率ですが、チームはまだギネスに正式に記録として認められていないとして、その最後の10桁が「7817924264」だったとだけ述べています。どうやって確認するのかはわかりませんが、ギネスがその数値を正しいと認め、記録として認定すれば、62.8兆桁すべてを公表するとしています。

という状態のようです。そもそもギネス側はどうやって検算するんでしょうか。
この路線のままでいけば計算性能の向上によって順当に伸びていく気はしますが、新たなブレイクスルーで一気に京の桁に突入する...なんてこともあるかもしれません。
それではこのへんで。

参考リンク

本文中でも適宜紹介していますが、改めて参考リンクです。

今回記事でChudnovskyの公式を用いた実装としては、こちらの記事にあるものをほぼそのまま利用させていただきました。

こちらはCで書かれていますが、1億桁を目指した奮闘記です。

あとは円周率の求め方いろいろ。今回使ったもののほかにもいろいろありますね。見てて楽しい。