本記事では準同型暗号として用いられる格子暗号の1種であるCKKS形式の中身をつかむことを目指します。こちらの英語記事をもとに作成しており、この記事を噛み砕いた日本語バージョンの説明を作るつもりで記事を書いています。
準同型暗号とは
データを暗号化したまま計算することができる技術です。この技術を応用することにより安全なデータ分析を実現することができます。イメージ図だけを示し詳細は省きます。
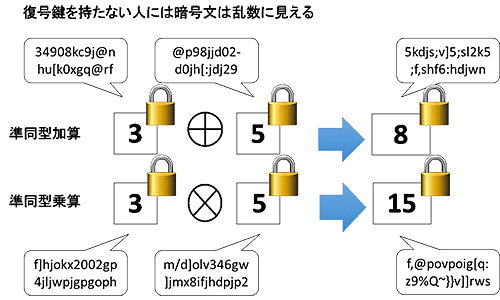
画像元
格子暗号とは
準同型暗号の1種です。準同型暗号としては他にもRSA暗号やPaillier暗号などがありますが、その中でも格子暗号は現在非常に活発に研究が行われている暗号です。格子暗号の実現方式として他にもBFV方式やTFHE方式などが存在しますが、今回はCKKS形式を取り上げます。3つの暗号化方式にはいくつか違いが存在しますが、抑えておくべき要点としてCKKS形式は
- 複素数を扱うことができる(実数が扱えるわけだが、BFV方式は整数しか扱えない)
- 計算により誤差が生じる(TFHE形式やBFV方式には誤差が存在しない)
という性質を持ちます。
CKKS形式のフレームワーク
CKKS形式は以下のようなプロセスをとります。(詳細は後ほど見ていきます)
- encode
- 平分の内容を表す複素数ベクトルを整数係数多項式に変換します。
- encrypt
- 整数係数多項式暗号化して整数係数多項式のペアからなる暗号文を得ます。
- calculate
- 行いたい計算を暗号化状態で行います。
- decrypt
- 計算結果を復号して整数係数多項式を得ます。
- decode
- 整数係数多項式を複素数ベクトルに変換して最終的に求めたかった結果を得ます。
格子暗号は多項式を暗号文や公開鍵、秘密鍵として扱います。一般に平文はn進数の数字の並び(すなわちベクトル)として扱われますが、これを多項式に変換する必要があります。そのためにencode処理を行います。
冒頭で紹介した記事にわかりやすい図があったので貼ります。

以後はそれぞれを深く見ていきます。
encode/decode
ナイーブなencode
平分の複素数ベクトルから多項式に変換することを考えます。
$\xi = e^{\frac{\pi i}{N}}$とします。これを用いてvandermonde行列$A_{ij} = \xi ^{(2i-1)(j-1)} \in \mathbb{C} ^{N \times N}$を作ります。その後、平分の複素数ベクトル$b\in \mathbb{C} ^N$に対して$Ax=b$を解きます。そのとき得られる解ベクトル$x\in \mathbb{C}^N$の各要素の値を係数に持つ$n$次多項式$p$を作成することで、平分の複素数ベクトルから多項式に変換することができます。
ナイーブなdecode
$b_i = p(\xi ^{2i-1}) \in \mathbb{C}^N$とすることで多項式$p$から複素数ベクトル$b$にdecodeすることができます。実際に手を動かしてもらえるとわかりますが、平分$b$に対してencodeを行った直後にこのdecodeを行うと、結果として$b$にほとんど一致する複素数ベクトルが得られます。(そうでないと困りますよね)
このナイーブなdecodeの写像を$\sigma$と呼ぶことにします。多項式$p$からdecodeして得られる複素数ベクトルは$\sigma(p)$と表されます。
example
$b = [1, 2, 3, 4]$をencodeすると
p = (2.5+4.4e^{-16}j)+(-5.0e^{-16}+\frac{\sqrt{2}}{2}j)x+(-3.5e^{-16}+0.5j)x^2 + (-8.3e^{-16}+\frac{\sqrt{2}}{2}j)x^3
が得られるそうです。これをdecodeすると
b^{\prime} = [1-1.1e^{-16}j, 2-4.7e^{-16}j, 3+2.8e^{-17}j, 4+2.2e^{-16}j]
が得られるそうです。(冒頭で紹介した記事参照)
ただ、この方式だと得られる多項式は複素数係数多項式となります。実はこれでは準動型暗号として使用するにあたっては十分な性質を満たしません。上の図にあるようにencode後は整数係数多項式になる必要があります。なのでこのencode/decode方式を微妙に調整します。
encode
- 平分の複素数ベクトル$z \in \mathbb{C} ^{\frac{N}{2}}$に対して$\pi ^{-1}(z) = [z_1,\cdots, z_{\frac{N}{2}}, \overline{z_{\frac{N}{2}}}, \cdots, \overline{z_{1}} ]\in \mathbb{C} ^N$を求めます。
- 巨大な整数$\Delta _{scale}$を用意し、掛け算を行い$z^{\prime} = \Delta _{scale} \pi ^{-1}(z)$を求めます。($\Delta _{scale}= 2^{30}$程度の規模感でscalingを行います。)
- $(b_1,\cdots , b_N) = (\sigma(1), \cdots , \sigma(x^{N-1}))$として(ナイーブなdecodeにもありますが$\sigma$は多項式をナイーブにdecodeした結果のベクトルを表します。)
b = \sum _{i=1} ^{N} \frac{<z_i, b_i>}{||b_i||^2} b_i
と$b_i$の線形和で表します。その後、各係数$\frac{ < z_i , b_i> }{ ||b_i||^2 }$を整数に丸めることで$b^{\prime}$を得ます。($< a, b >$はaとbの内積を表します。)
4. ナイーブなencodeで説明した方法で$Ax = b^{\prime}$の解を係数とする多項式を$p$とすると、これは整数係数多項式です。
decode
- 多項式$p$に対して$\Delta _{scale} ^{-1} p $を計算します。
- 得られた$\Delta _{scale} ^{-1} p $にたいしてナイーブなdecodeを実行して複素数ベクトル$z^{\prime} \in \mathbb{C} ^N$を得ます。
- ベクトルの前半分の要素を抜き出して平分$z \in \mathbb{C}^{\frac{N}{2}}$を得ます。
(平分$z$に対してencode/decodeを行うと、ほとんど$z$に一致する複素数ベクトルが得られます。)
注意点
平分の複素数ベクトルは$\mathbb{C} ^{\frac{N}{2}}$ですが、このとき$N=2^{14}$程度とします。多くの場合、平文を表す場合それほどのビットは必要ありません。なので空きビットには0を入れます。$N$は大きな値であるほうがよいのですが、$N$は2のべき乗とすることが多いです。これは高速フーリエ変換のアルゴリズムを利用して暗号文状態での掛け算を高速に行うためです。
scaleを行う理由についてですが、これは整数に丸める操作を行う際の誤差を少なくするためです。1.456を小数第一位で整数に丸める例を考えます。scaleを行わない場合、1.456は1に丸められます。一方で1.456を100倍にscaleした後に丸めると146になります。これを100でrescaleすると1.46になります。準同型暗号として機能させるためには整数係数多項式にencodeする必要があり、そのためには丸め操作を行うことが必要です。その誤差を減らすために大きな数で掛け算をする処理を施しています。
encode exmaple
$z = [3+4j, 2-j]$から$\pi ^{-1} (z) = [3+4j, 2-j, 2+j, 3-4j]$を得ます。
$\Delta _{scale} = 64$として$z ^{\prime} = [192+256j, 128-64j, 128+64j, 192-256j]$を得ます。
示したプロセスで$b^{\prime} = [192.53+256.17j, 127.47-63.83j, 127.47+63.83j, 192.53-256.17j]$を計算します。
これに対してナイーブなencodeを行い、実部を取り出すと整数係数多項式$p=160+91x+160x^2 + 45x^3$を得ます。
decode example
$p=160+91x+160x^2 + 45x^3$から$p^{\prime} = \Delta _{scale} ^{-1} p = 2.5+1.40625x+2.5x^2+0.71875x^3$を得ます。
この多項式に対してナイーブなdecodeをすることで$z^{\prime} = [2.997+3.992j,2.003-1.008j, 2.003+1.008j, 2.997-3.992j]$を得ます。
この配列の前半半分を抜き出すことで$z =[2.997+3.992j,2.003-1.008j]$を得ます。(元の平分に近い値ですね。)
encrypt/decrypt
encrypt/decryptに関してはこちらの記事が参考になりますので、そちらをご参照ください。
理解の足しになるかもしれないので以前私が書いた記事のリンクも貼っておきます。
calculate
足し算と掛け算については上の記事を見てもらえると基本的な計算方法と複合した結果が本来の計算結果になることも確認できます。しかし実は掛け算を行った後にはrelinearlizationと呼ばれる少し特殊な処理をしなければなりません。
relinearlization
復号する際は暗号文$(c_0 , c_1)$と秘密鍵$s$に対して$c_0 + c_1 s$を計算し、その各係数にたいして剰余をとることでdecryptを行います。
足し算をした結果を復号する場合を考えます。この際暗号文同士で足し算を行った後、復号するわけですが、これは2つの暗号文$c =(c_0 , c_1), c^{\prime} =(c_0 ^{\prime} , c_1 ^{\prime})$に対して$(c_0 + c_0 ^{\prime}) + (c_1 +c_1 ^{\prime})s$を復号することになります。これを実行する際には特に問題がありません。実際に意図した計算結果を得ることができます。
次に掛け算した結果を復号する場合を考えます。
暗号文に対して掛け算を行いたいとき、$(c_0 + c_1 s)(c_0 ^{\prime} + c_1 ^{\prime} s)=c_0 c_0 ^{\prime} + (c_0 c_1 ^{\prime} + c_1 c_0 ^{\prime})s + c_1 c_1 ^{\prime} s^2$を計算して、これを復元することになります。つまり掛け算を行うと、多項式を$s$の次数が増えることになります。この状態で更に掛け算を行うと次数は2のべき乗のスピードで増えていきます。すなわち掛け算を行うと暗号文のサイズが指数関数的に増えていってしまうことになってしまいます。なので掛け算を行ったあとに暗号文のサイズを抑えるために多項式の$s$の次数を抑える処理が必要になります。具体的には掛け算の後に$s$の2次式になっているものを$s$の一次式として表し直してやる必要があります。$s$の一次式、すなわち線形関数として表し直すのでrelinearlizationと呼びます。
rescale
relinearlization以外にも掛け算の際には注意が必要です。そもそも暗号化の際にscale値$\Delta _{scale}$で大きくしていますが、掛け算を行うと$\Delta _{scale} ^2$の大きさになります。このまま掛け算を続けるとscaleが拡大し続けていしまいます。これを防ぐためにrescaleと呼ばれる処理も必要になります。
まとめ
今回は格子暗号の1形式であるCKKS形式に注目をして話を進めました。詳細な点は冒頭で紹介した記事にもありますので適宜ご確認いただけるとありがたいです。