7人の人間がそれぞれ総当たりで2人対戦を行う場合、全部で何試合あるでしょうか?
全部で21試合です。
総当たり数は 6+5+4+3+2+1 で計算できます。
では3人対戦の場合はどうでしょうか?
(答えは一番下に書いてあります)
このような場合の総当たりパターンを生成出来るクラスを作ってみたいと思います。
ちなみに上記の2人対戦のパターンであれば、こんな感じで組むと、
for (int a = 0; a < (7 - 1); a++)
{
for (int b = (a + 1); b < 7; b++)
{
printf("(a=%d,b=%d) ", a, b);
}
printf("\n");
}
こんな感じで列挙が出来ます。
(0,1) (0,2) (0,3) (0,4) (0,5) (0,6)
(1,2) (1,3) (1,4) (1,5) (1,6)
(2,3) (2,4) (2,5) (2,6)
(3,4) (3,5) (3,6)
(4,5) (4,6)
(5,6)
これを総人数や対戦人数を臨機応変に変更できるようにクラス化してみます。
# pragma once
# include <vector>
# include <stdarg.h>
class BruteForceSearch
{
public:
BruteForceSearch()
:m_pBuffer(nullptr) {}
virtual ~BruteForceSearch() {
Reset();
}
void Reset();
void SetMassNum(const std::vector<int>& nums);
void Run(int num);
protected:
char* m_pBuffer;
int m_TotalMassNum;
std::vector<int> m_Axis;
int m_HierarchyCount;
virtual int Confirm();
void Dump();
int SubFunc(int ptNum, int start, int end);
};
# include "BruteForceSearch.h"
// リセット
void BruteForceSearch::Reset()
{
delete[] m_pBuffer;
m_pBuffer = nullptr;
}
// マス数の設定
void BruteForceSearch::SetMassNum(const std::vector<int>& nums)
{
m_Axis = nums;
m_TotalMassNum = 1;
for (auto num : m_Axis)
{
m_TotalMassNum *= num;
}
m_pBuffer = new char[m_TotalMassNum];
memset(m_pBuffer, 0, m_TotalMassNum);
}
// 実行
void BruteForceSearch::Run(int num)
{
if (m_pBuffer == nullptr)
{
return;
}
memset(m_pBuffer, 0, m_TotalMassNum);
m_HierarchyCount = 0;
SubFunc(num, 0, m_TotalMassNum);
}
// 確定
int BruteForceSearch::Confirm()
{
Dump();
return 0;
}
// 状態表示
void BruteForceSearch::Dump()
{
auto axisSize = m_Axis.size();
auto bFlag = false;
putchar('(');
for (auto i = 0; i < m_TotalMassNum; i++)
{
if (m_pBuffer[i] != 0)
{
if (bFlag)
{
putchar(',');
}
if (axisSize != 1)
{
putchar('(');
auto tmp = i;
for (size_t j = 0; j < axisSize; j++)
{
if (j != 0)
{
putchar(',');
}
printf("%d", tmp % m_Axis[j]);
tmp /= m_Axis[j];
}
putchar(')');
}
else
{
printf("%d", i);
}
bFlag = true;
}
}
puts(")");
}
int BruteForceSearch::SubFunc(int ptNum, int start, int end)
{
if (ptNum == 0)
{
return Confirm();
}
for (auto i = start; i < (end - (ptNum - 1)); i++)
{
if (ptNum == 1)
{
m_pBuffer[i] = 1;
auto result = Confirm();
m_pBuffer[i] = 0;
if (result != 0)
{
return result;
}
}
else
{
m_pBuffer[i] = 1;
m_HierarchyCount++;
auto result = SubFunc(ptNum - 1, i + 1, end);
m_pBuffer[i] = 0;
if (result != 0 && result <= m_HierarchyCount)
{
m_HierarchyCount--;
return result;
}
m_HierarchyCount--;
}
}
return 0;
}
総人数が増える分には変更は少しですが、対戦人数が増えるとループの入れ子が増えるので、実装の仕方が少し複雑になります。
再帰を使って表現します。
使い方はこんな感じです。
int main()
{
BruteForceSearch cls;
std::vector<int> axis;
axis.push_back(7);
cls.SetMassNum(axis);
cls.Run(2);
return 0;
}
SetMassNum関数には、上記の例で言えば人数を指定します。
なんでこんなややこしい指定なのかは後で書きます。
Run関数でパターンを列挙していきます。
引数には、上記の例で言えば対戦人数になります。
基本クラスでは、標準出力にパターンを表示します。
独自に何かチェックを行いたい場合は、クラスを継承してConfirm()をオーバーライドします。
やっていることの考え方
このクラスでは、必要な数だけマス(m_pBuffer)を用意して0でまず埋めます。
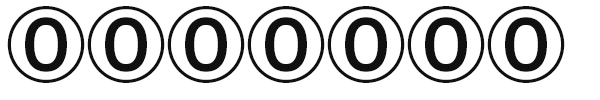
そしてRun()で指定された数だけマスを1にして、Confirm()を呼び出します。
Run(2)の場合の最初のConfirm()呼び出しではm_pBufferは図のようになっています。
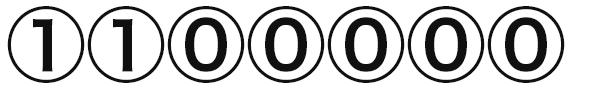
そうしてm_pBufferの中を書き換えながら、Confirm()が21回呼び出されます。
先程の
std::vector<int> axis;
axis.push_back(7);
cls.SetMassNum(axis);
ですが、
std::vector<int> axis;
axis.push_back(4);
axis.push_back(3);
cls.SetMassNum(axis);
という感じにすると、

といった感じの2次配列のマス目でパターンを表現することが出来ます。
n×mマスの中から3マスを塗りつぶした際に、2つのマス同士が上下左右にくっついてしまうパターンがいくつあるか答えよ
みたいな問題などで使用します。
総当たりアルゴリズムの欠点は、数が増えるとチェック対象が爆発的に増えていくことです。
上記の例でも10×10程度のマスなら大丈夫でも11×11になった途端、急に結果が出るまでに時間がかかるようになったりします。
何かのチェックを行っている場合は、足切り(これ以降の無駄なチェックをスキップ)をする事で処理時間を短縮することが出来ますが、一応Confirmが0以外を返した場合は、それより後ろのチェックをスキップできるようになっていますので、足切りできる場合は使ってみてください。
総当たりはパズルを解く際の一番基本的なロジックです。
とてもシンプルでミスの少ない考え方ですので、まずは総当たりでサンプルをいくつか採って、法則を見つけていくのが良いでしょう。
*7人の人間がそれぞれ総当たりで3人対戦を行う場合の総試合数は35試合です。