対数二項回帰モデル
二値応答のデータを扱う場合に頻用される統計モデルとして,ロジスティック回帰モデルがあります.
ロジスティック回帰モデルは,応答の分布を二項分布,リンク関数をロジットとした一般化線型モデルです.
一方で,リンク関数としてロジットの代わりに対数関数を用いた一般化線型モデルが使用されることもあり,対数二項回帰モデルとよばれます.
対数二項回帰モデルの回帰係数の最尤推定には,フリーの統計ソフトRや,有償の統計ソフトSASを利用することができます.
しかし,それぞれのソフトウェアの出力において,標準誤差の推定値として異なった値が出力されてしまうことから,注意が必要です.
本ページでは,Rのglm関数を利用した場合とSASのGENMODプロシジャを利用した場合の標準誤差の出力の差異を比較し,差異の原因について考察します.
使用データ
R言語に付属するデータinfertを用います.
library(tidyverse)
data(infert)
dat <- infert %>%
mutate(spont = if_else(spontaneous==0, 0, 1)) %>%
select(age,case,spont)
write.csv(dat, "~/infert.csv", row.names=FALSE)
データの変数と中身は次のようになっています.
# age:年齢(歳)
# case:不妊症か否かを表す(0/1).
# spont:自然流産歴を表す(0/1).元のデータは「0回/1回/2回以上」だったが,「0回/1回以上」に変換.
> head(df)
age case spont
1 26 1 1
2 42 1 0
3 39 1 0
4 34 1 0
5 35 1 1
6 36 1 1
RとSASでの結果の差異
Rのglm関数を用いた場合とSASのGENMODプロシジャを用いた場合で,回帰係数の推定値は一致するが標準誤差については一致しないことがわかります.
推定された標準誤差は,SASの方がやや大きめです.
Rのglm関数による実装と出力
fit <- glm(case ~ spont + age,
data=dat,
family=binomial(link="log"))
> summary(fit)
Call:
glm(formula = case ~ spont + age, family = binomial(link = "log"),
data = d)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.3562 -0.7259 -0.6446 1.0890 1.9084
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.30574 0.54582 -4.224 2.40e-05 ***
spont 0.99621 0.19364 5.145 2.68e-07 ***
age 0.02108 0.01576 1.337 0.181
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 316.17 on 247 degrees of freedom
Residual deviance: 287.28 on 245 degrees of freedom
AIC: 293.28
Number of Fisher Scoring iterations: 7
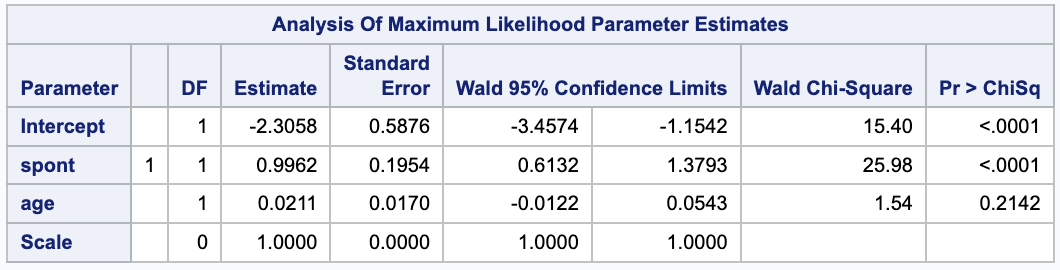
SASのGENMODプロシジャによる実装と出力
FILENAME REFFILE '/file_path/infert.csv';
PROC IMPORT DATAFILE=REFFILE
DBMS=CSV
OUT= WORK.infert;
GETNAMES=YES;
DATAROW=2;
RUN;
PROC GENMOD DATA=WORK.infert;
CLASS spont(param=ref ref=first);
MODEL case(event="1") = spont age / dist = binomial link=log itprint;
ESTIMATE "RR(spont)" intercept 0 spont 1 age 0/e exp;
RUN;
ソフトウェア間での標準誤差計算方法の差異
多くの統計計算パッケージでは,情報行列に基づいて最尤推定値の標準誤差が計算されます.そこで,まず,対数二項回帰モデルでの情報行列の形式を具体的にみていくことにします.
記法を
- $y_{i} \in \left\lbrace0,1\right\rbrace ,(i=1,\ldots,n)$:二値の応答変数
- $\boldsymbol{x}_{i} \in \mathbb{R}^{p}$:説明変数ベクトル (説明変数は定数)
\boldsymbol{x}_{i}=(x_{i, 0},\ldots,x_{i, p-1})^{\top}
- $\mathbf{X} \in \mathbb{R}^{n \times p}$:説明変数行列
\mathbf{X}=(\boldsymbol{x}_{1},\ldots,\boldsymbol{x}_{n})^{\top}
- $\boldsymbol{\beta} \in \mathbb{R}^{p}$: 回帰係数ベクトル
\boldsymbol{\beta}=({\beta}_{0},\ldots,{\beta}_{p-1})^{\top}
と導入すると,対数二項回帰モデルの対数尤度$\ell(\boldsymbol{\beta})$は
\begin{align*}
\ell(\boldsymbol{\beta})
&= \sum_{i=1}^{n} \left\{
\boldsymbol{x}_{i}^{\top}\boldsymbol{\beta} y_{i}
+ (1 - y_{i})\log \left(1 - \exp (\boldsymbol{x}_{i}^{\top}\boldsymbol{\beta})\right)
\right\}
\end{align*}
と表せます.
対数尤度のヘッセ行列(パラメータによる二階微分)の負をとることで観測情報行列$\mathbf{J}{(\boldsymbol{\beta})}$を計算すると
\begin{align*}
\mathbf{J}{(\boldsymbol{\beta})}
&= -\frac{\partial^{2}}{\partial \boldsymbol{\beta}^{\top} \partial \boldsymbol{\beta}} \ell(\boldsymbol{\beta})
= -\mathbf{X}^{\top} \mathbf{W}_{\mathbf{J}}(\boldsymbol{\beta})\mathbf{X},
\\
\mathbf{W}_{\mathbf{J}}(\boldsymbol{\beta})
&= \mathrm{diag}({w}_{1},\ldots,{w}_{n})^{\top},
\\
w_{i}
&= -\frac{(1 - y_{i})\exp (\boldsymbol{x}_{i}^{\top}\boldsymbol{\beta})}{\left(1 - \exp (\boldsymbol{x}_{i}^{\top}\boldsymbol{\beta})\right)^{2}}
\end{align*}
が得られます.
さらに,フィッシャー情報行列$\mathbf{I}{(\boldsymbol{\beta})}$は
\begin{align*}
\mathbf{I}{(\boldsymbol{\beta})}
&= \mathbb{E}_{y} \left[-\frac{\partial^{2}}{\partial \boldsymbol{\beta}^{\top} \partial \boldsymbol{\beta}} \ell(\boldsymbol{\beta})\right]
= -\mathbf{X}^{\top} \mathbf{W}_{\mathbf{I}}(\boldsymbol{\beta})\mathbf{X},
\\
\mathbf{W}_{\mathbf{I}}(\boldsymbol{\beta})
&= \mathrm{diag}({\omega}_{1},\ldots,{\omega}_{n})^{\top},
\\
\omega_{i}
&= -\frac{\exp (\boldsymbol{x}_{i}^{\top}\boldsymbol{\beta})}{1 - \exp (\boldsymbol{x}_{i}^{\top}\boldsymbol{\beta})}
\end{align*}
と得られます.
さて,観測情報行列とフィッシャー情報行列をそれぞれRで実装し,その逆行列の対角成分の平方根を計算すると,次の結果が得られます.
y <- d$case
X <- d %>%
mutate(const=1) %>%
dplyr::select(const,spont,age) %>%
as.matrix()
p <- fit$fitted.values
# 観測情報行列
W.J <- diag(
-(1-y)*p/((1-p)^2)
)
J <- - t(X) %*% W.J %*% X
# フィッシャー情報行列
W.I <- diag(
-p/(1-p)
)
I <- - t(X) %*% W.I %*% X
> sqrt(diag(solve(J)))
const spont age
0.58757012 0.19543400 0.01697029
> sqrt(diag(solve(I)))
const spont age
0.5458181 0.1936362 0.0157587
RおよびSASでの回帰係数の標準誤差の推定結果と比較すると,観測情報行列に基づく計算結果はSASでの結果に,フィッシャー情報行列での計算結果はRでの結果に一致します.
したがって,Rのglm関数を利用した場合とSASのGENMODプロシジャを利用した場合の標準誤差の出力の差異は,観測情報行列とフィッシャー情報行列のどちらに基づいて標準誤差が計算されるかに起因すると考えられます.
実際に,SASのGENMODプロシジャのドキュメントでは,対数尤度のヘッセ行列の逆行列の負をそのまま用いて標準誤差を計算していることが記載されています.
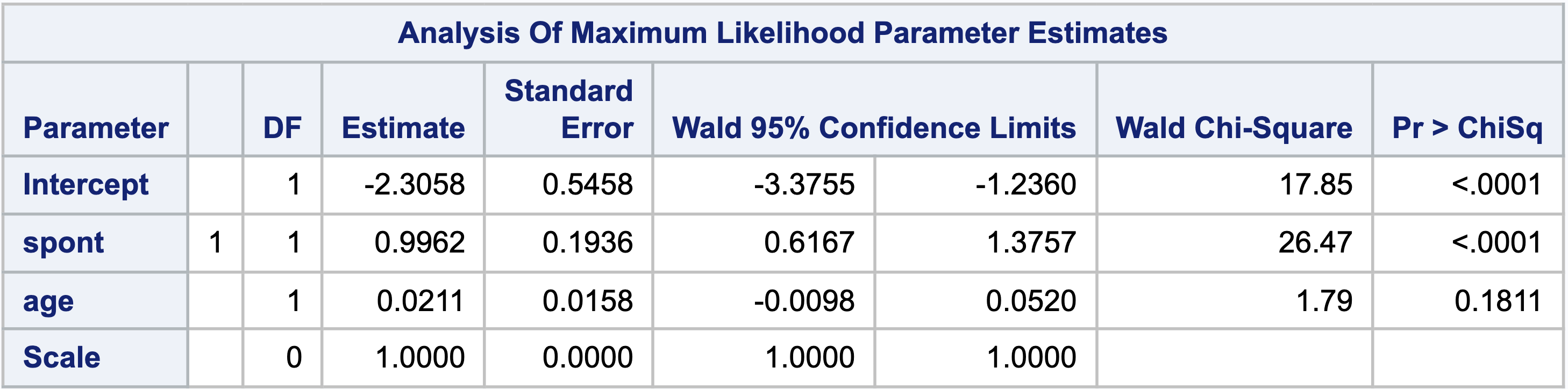
SASでフィッシャー情報行列に基づく推定値を得る方法
本ページを X(twitter)でポストしたところ,@triadsou 先生より,SASのGENMODプロシジャでSCORINGオプションに大きな数字を指定すればRと同じ結果になるのではないかという指摘がありました.
GENMODプロシジャでは,MODELステートメント内でSCORING=number(numberは0以上の整数)を指定することで,推定値の計算アルゴリズムにおいて,number回目の反復までヘッセ行列の逆行列の代わりにフィッシャー情報行列が使用されます(cf. SCORINGオプションのドキュメント).
したがって,number回目までに推定値の計算が収束すれば,最後の反復で使用されたフィッシャー情報行列に基づいて標準誤差が推定されると考えられます.
そこで,推定値の計算アルゴリズムの最大反復回数(GENMODプロシジャでは50回)をSCORINGオプションに指定して計算を実行してみると,次のように,実際にRの結果と一致する結果を得ることができました.
PROC GENMOD DATA=WORK.infert;
CLASS spont(param=ref ref=first);
MODEL case(event="1") = spont age / dist = binomial link=log itprint scoring=50;
ESTIMATE "RR(spont)" intercept 0 spont 1 age 0/e exp;
RUN;