目的変数:予測したい情報
説明変数:予測に使う情報
モデル:説明変数と目的変数を結ぶ”箱”(数式やプログラム)
目的変数の方に応じて問題の種類が変わる
- 目的変数が数値型 ⇒ 回帰問題 (ex.売上予測)
- 目的変数がID型 ⇒ 分類問題(ex.クリック予測(クリックする or しない))
目的変数の有無に応じて機械学習は以下の2種類にわけられる
- 目的変数がある:教師あり学習 : 正解があって機械学習モデルで求める
- 目的変数がない:教師なし学習 : データからパターンを見つけたい。
教師あり学習-回帰-
以下において、線形回帰分析(linear regression)以外は非線形回帰分析(nonlinear regression)。
線形回帰では線形パラメータが必要だが、非線形回帰では必要ない。線形パラメータとの関係を適切にモデル化できない場合は、線形回帰ではなく非線形回帰を使用する。
| モデル | 説明 | イメージ |
|---|---|---|
| 線形回帰分析 | ”線形”とは線で解けることを意味する。回帰の場合、目的変数:説明変数のグラフを書くと線になる。 |
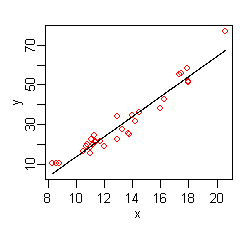 wikipediaより引用 wikipediaより引用 |
| MARS(Multivariate adaptive regression splines) | 部分的に線形モデルを作ってる感じ。 |
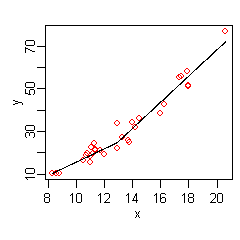 wikipediaより引用 wikipediaより引用 |
| サポートベクター回帰(SVR) | サポートベクターマシンの考え方を利用している。 |
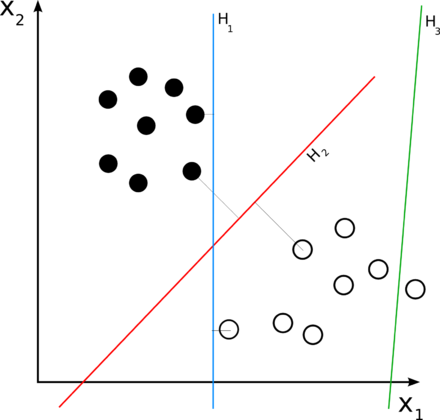 wikipediaより引用 wikipediaより引用 |
| 回帰木 | ツリー状に分類していく。リーフの平均値が枝の値。離散的な値しか予測できない。データがグループ分けされていく。 |
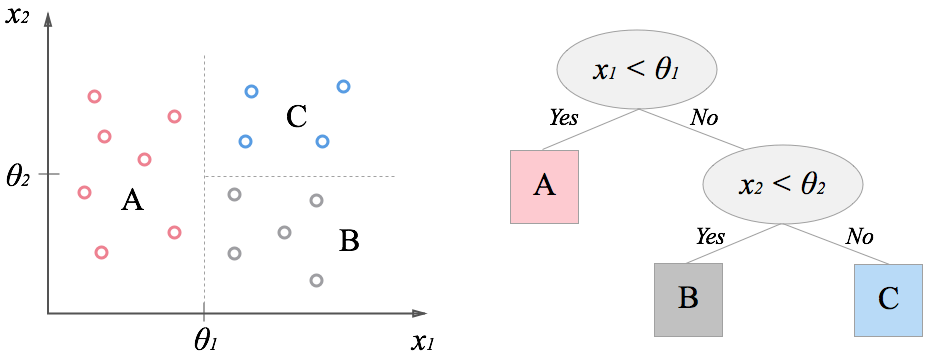 引用元:http://codecrafthouse.jp/wp-content/uploads/2014/09/decisiontree1.png 引用元:http://codecrafthouse.jp/wp-content/uploads/2014/09/decisiontree1.png
|
| モデル木 | モデル木は回帰木に似ているが、 回帰木が予測値として端末ノードの平均値を利用するのに対して、 モデル木の場合は線形回帰モデルで予測値を求める。 | |
| 遺伝子プログラミング | どういうモデルをするか推定する。進化論を真似している。最初に適当な乱数で非構造を作って、それに対して演算。試行回数を増やさないといい結果は得られない |
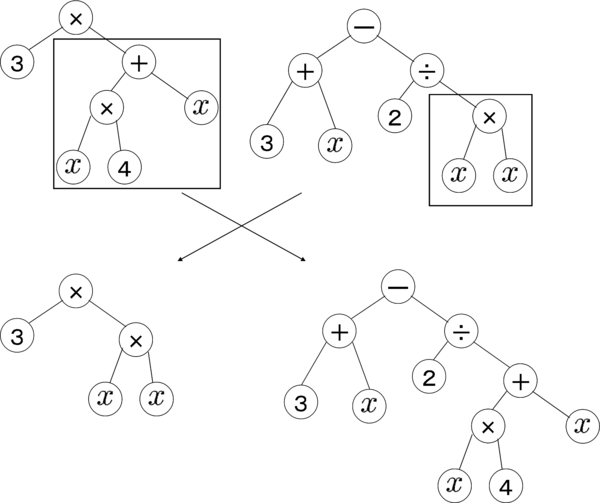 wikipediaより引用 wikipediaより引用 |
教師あり学習-分類-
| モデル | 説明 | イメージ |
|---|---|---|
| 二値分類 | シンプルな方法。データを二種類に分類する。 | 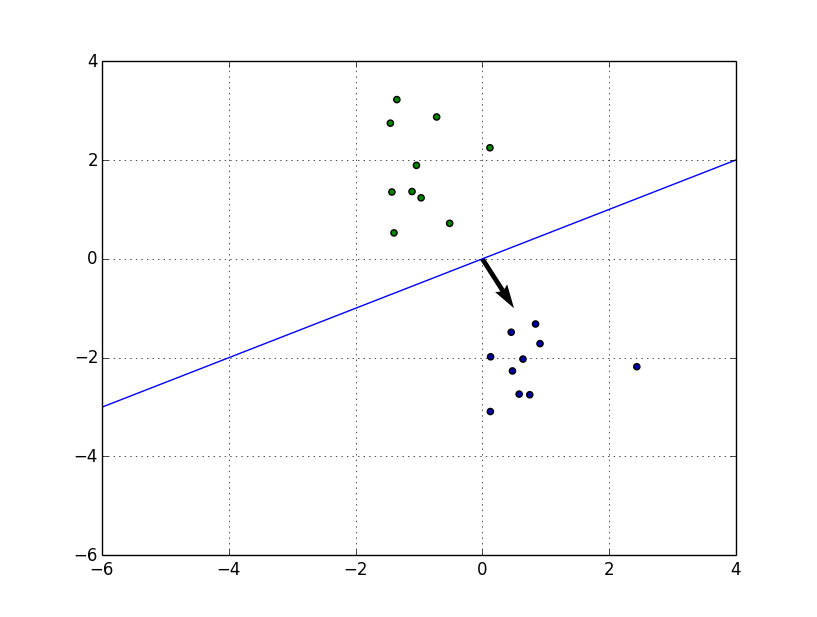 |
| ロジスティック回帰 | を直線の代わりにシグモイド曲線(S 字状曲線)で回帰する手法 |
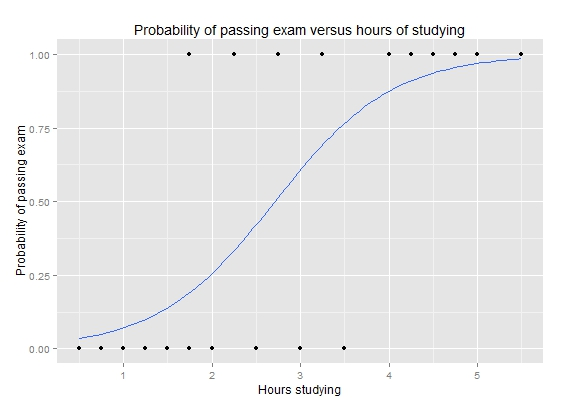 wikipediaより引用 wikipediaより引用 |
| k近傍法 | 学習データをベクトル空間上にプロットしておき、未知のデータがそこから距離が近い順に任意のK個を取得し、多数決でデータが属するクラスを推定する。 |
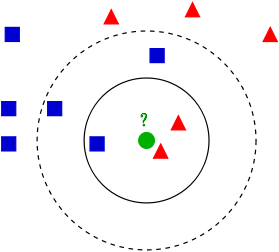 wikipediaより引用 wikipediaより引用 |
| サポートベクターマシン(SVM) | カーネル関数を用いて線形分離ができないものを特徴空間にマッピングを行い分離することができるようにしている。カーネルの種類は4つ(linear,polynomial,rbf,sigmoid)ある。 |
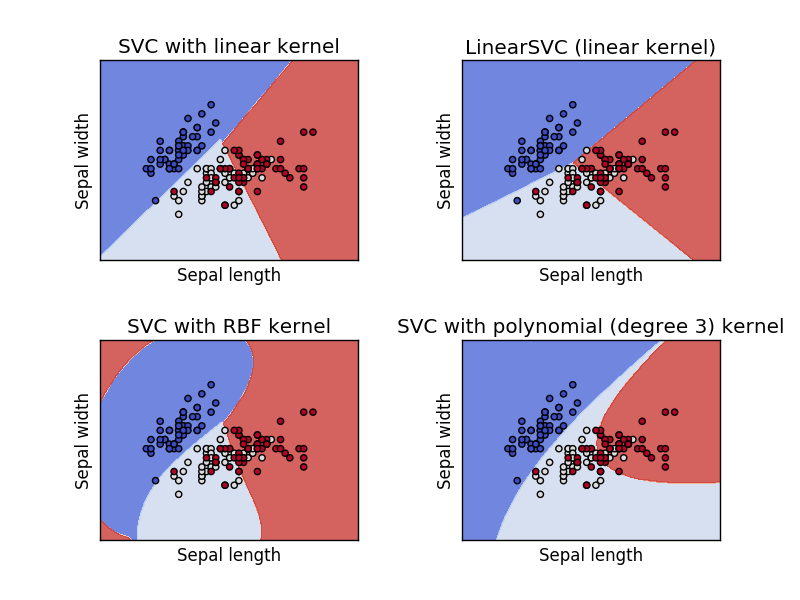 http://scikit-learn.org/stable/modules/svm.html https://www.youtube.com/watch?v=3liCbRZPrZA http://scikit-learn.org/stable/modules/svm.html https://www.youtube.com/watch?v=3liCbRZPrZA
|
| 決定木 | ツリー状に分類。 |
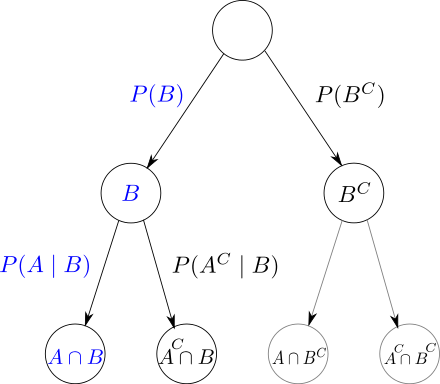 引用元:https://ja.wikipedia.org/wiki/%E6%B1%BA%E5%AE%9A%E6%9C%A8 引用元:https://ja.wikipedia.org/wiki/%E6%B1%BA%E5%AE%9A%E6%9C%A8
|
| ランダムフォレスト | 木をいっぱい作る。木の形ばらばら。予測するときは多数決。分類はされて正解率は高いが、なんでこのような結果になるのかその理由は分からないのが欠点。 | |
| ニューラルネット | 人間の脳の神経回路の特性を計算機上のシミュレーションによって表現することを目指した数学モデル。 |
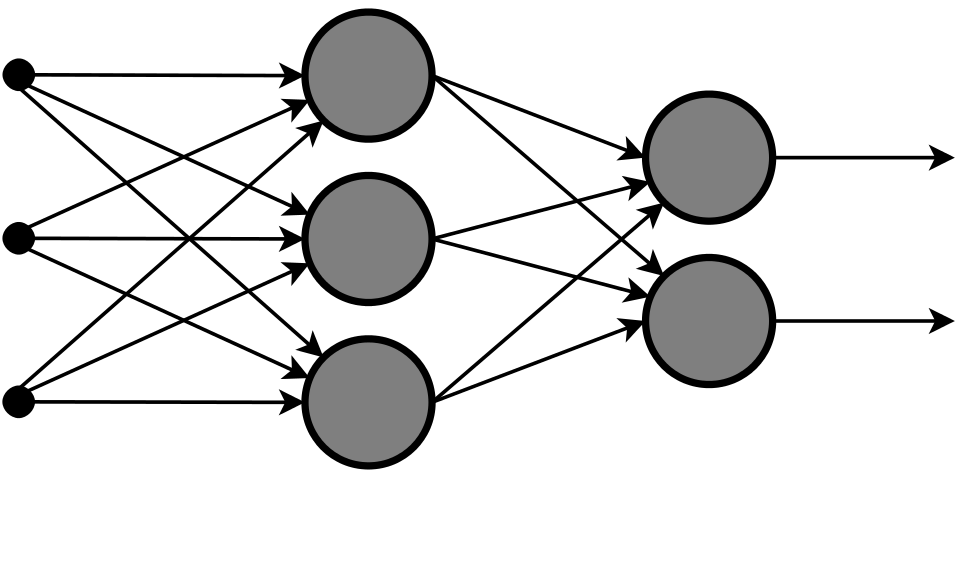 wikipediaより引用 wikipediaより引用 |