クラスター分析の特徴
- 最も似ている組み合わせから順番にクラスターにしていく方法
- 近いものから順番にまとめるという方法をとるので、あらかじめクラスター数を決める必要がない。
- 分類の対象が非常に多い場合、計算量が多くなり実行が困難になったり、出来上がる樹形図が巨大になり結果が不明瞭になる。
重心法
- 重心法は、以下のような流れで実装される。
0: データ準備(標準化)
- 体重をグラムに直すと値が1000倍になってしまい、体重の変数の影響が大きくなってしまう。そのため、標準化を行い単位の影響をなくす。
- ここでは平均0、分散1で標準化を実施。
標準化前
| 動物 | 体重(kg) | 脳の重さ(g) |
|---|---|---|
| 牛 | 465 | 423 |
| 馬 | 521 | 655 |
| ゴリラ | 207 | 406 |
| 人間 | 62 | 1320 |
| チンパンジー | 52 | 440 |
標準化後
| 動物 | 体重(-) | 脳の重さ(g) |
|---|---|---|
| 牛 | 0.921 | -0.581 |
| 馬 | 1.175 | 0.016 |
| ゴリラ | -0.246 | -0.625 |
| 人間 | -0.902 | 1.727 |
| チンパンジー | -0.947 | -0.537 |
1: 変数を用いて個々の対象の距離を全て計算し、その中で距離が最も短い対象どうしを併合して最初のクラスターを作成する。
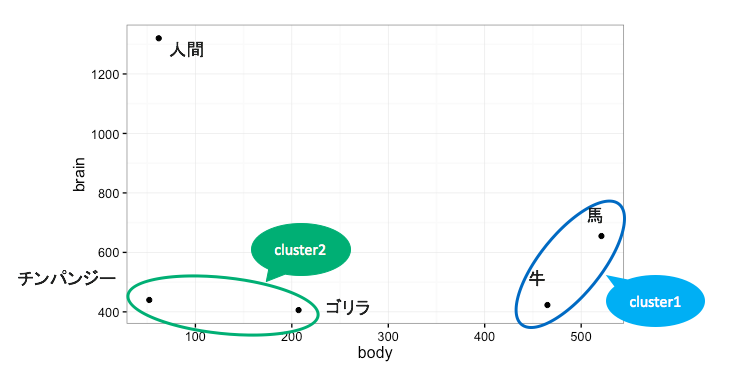
牛と馬の距離
√((0.921-1.175) ^2 + -0.581 -0.016) ^2 = 0.649
| 動物 | 牛 | 馬 | ゴリラ | チンパンジー |
|---|---|---|---|---|
| 馬 | 0.649 | |||
| ゴリラ | 1.168 | 1.159 | ||
| 人間 | 2.942 | 2.691 | 2.442 | |
| チンパンジー | 1.869 | 2.192 | 0.706 | 2.265 |
- その中で距離が最も短い対象どうしを併合して最初のクラスターを作成する。
→ 牛×馬の距離が最も短いため、これをcluster1とする
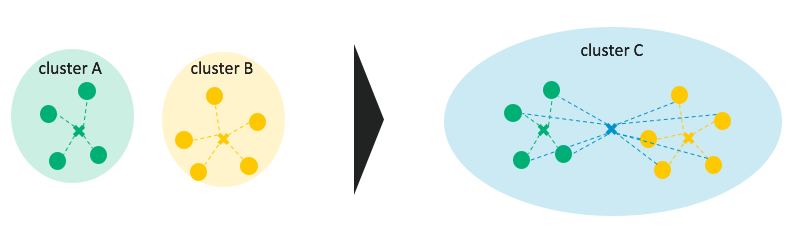
2: 1で作成されたクラスターと他の対象との距離を計算し、1で計算された対象間の距離を含めて、最も近いものを併合する。
- cluster1の体重と脳の重さは、牛と馬との重心(平均)を用いる。
- 体重:((0.921 + 1.175)/2) = 1.048
- 脳の重さ:((-0.581 +0.016)/2) = -0.283
| cluster1 | ゴリラ | 人間 | |
|---|---|---|---|
| cluster1 | 1.339 | ||
| ゴリラ | 2.800 | 2.442 | |
| 人間 | 2.011 | 0.706 | 2.265 |
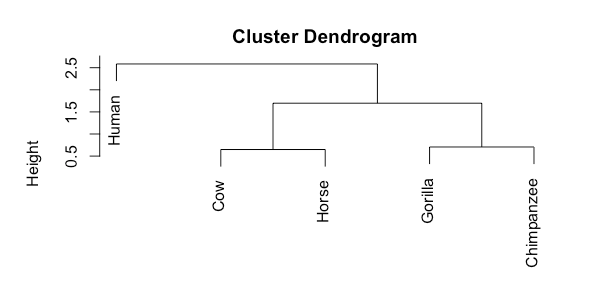
3. 手順2を繰り返し、全てのクラスターが併合されるまで計算を行う。
4. 計算結果を用いて、クラスターの併合される過程を表すデンドログラムを描く。
ウォード法
- 2つのクラスターを併合する際に、クラスター内の平方和を最小にするようにクラスターを併合していく手法
- クラスター間の距離を平方和(散布度)の増加量で表す。平方和はクラスター内の散らばりを表すため、併合後の平方和の増加量が大きければ、2つのクラスターは類似していないと考えられる。
- 鎖効果が起こりにくく、実用場面でも頻繁に利用される。
- 鎖効果
- ある1つのクラスターに対象がひとつずつ順番に吸収されて、クラスターの形成がなされていく現象。最短距離法で起こりやすい。
- 鎖効果