中心極限定理とは
wikiによると・・・
- 中心極限定理は、確率論・統計学における極限定理の一つ。
- 大数の法則によると、ある母集団から無作為抽出された標本平均はサンプルのサイズを大きくすると真の平均に近づく。これに対し中心極限定理は標本平均と真の平均との誤差を論ずるものである。多くの場合、母集団の分布がどんな分布であっても、その誤差はサンプルのサイズを大きくしたとき近似的に正規分布に従う。
- なお、標本の分布に分散が存在しないときには、極限が正規分布と異なる場合もある。
- 統計学における基本定理であり、例えば世論調査における必要サンプルのサイズの算出等に用いられる。
まとめると
- 母集団の分布がどんな分布であっても、その誤差はサンプルのサイズを大きくしたとき近似的に正規分布に従う。
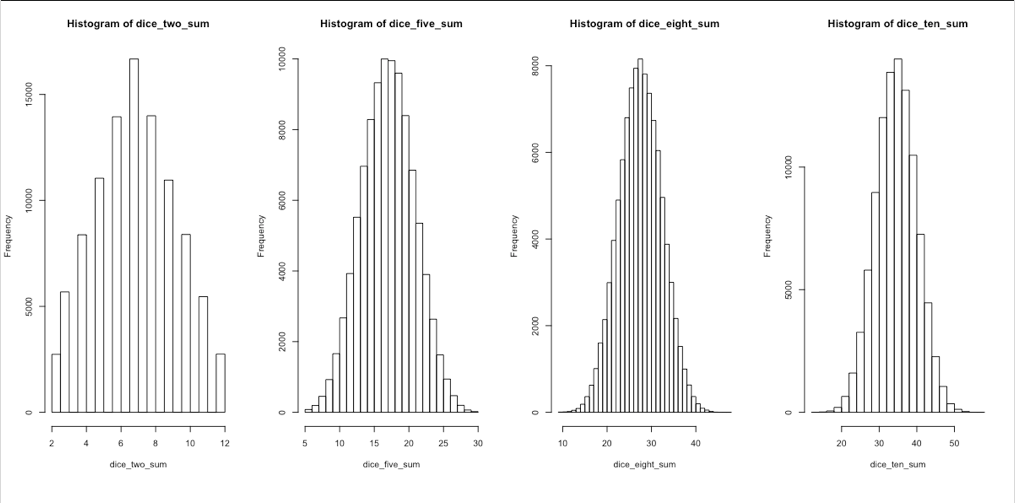
- 例えば、 n 個のサイコロを振って出た目の合計数の分布をとった時に、1個のサイコロでは、各目が出る確率はそれぞれ 1/6 、平均は 7/2 、分散は 35/12。サイコロの数 n が大きくなると,合計数の分布は正規分布に近づいていく。
R を使って試してみる
サイコロをN個投げて、その目の和がSとなる確率を求める。
> #サイコロ作成
> dice <- 1:6
> #データ表示
> dice
[1] 1 2 3 4 5 6
> #サイコロを2個投げることを100000回繰り返す
> dice_two_sum <- foreach(1:100000,.combine = "rbind") %do% {
> + sum(sample(dice,2,replace = TRUE))
> + }
> #ヒストグラム
> hist(dice_two_sum,breaks = 30)