図で見るソートアルゴリズム（C言語 / Java / VBA / Python）

はじめに

基本的なソートアルゴリズムについてまとめておきます（次の４つ）。

• ヒープソート
• クイックソート
• マージソート
• バブルソート

図表メインで、ソースコードは、C言語、Java、VBA、Pythonについて記載しています。
なお、JavaとPythonは初学レベルなので、もっと良い書き方があると思われます。ご注意ください。

最後は、気になる速度比較もしておきました。結果を見て、Pythonが人気がある理由がまた少し分かりました。

＜目次＞
1. ヒープソート
　1-1. ヒープソートのアルゴリズム概要
　1-2. ヒープソートのサンプルコード
2. クイックソート
　2-1. クイックソートのアルゴリズム概要
　2-2. クイックソートのサンプルコード
3. マージソート
　3-1. マージソートのアルゴリズム概要
　3-2. マージソートのサンプルコード
4. バブルソート
　4-1. バブルソートのアルゴリズム概要
　4-2. バブルソートのサンプルコード
5. 速度比較
　5-1. 計算量
　5-2. 処理速度の計測結果
　5-3. 【参考】処理時間計測のソースコード

1. ヒープソート

ヒープソートは、二分ヒープの性質を利用して並べ替えを行うアルゴリズムです。

二分ヒープは、次のような木構造を取ります。
要件は「完全二分木」であることと「親要素は子要素より常に大きいか等しい構造（ヒープ構造）」であることの2つです。

二分ヒープと配列のイメージ

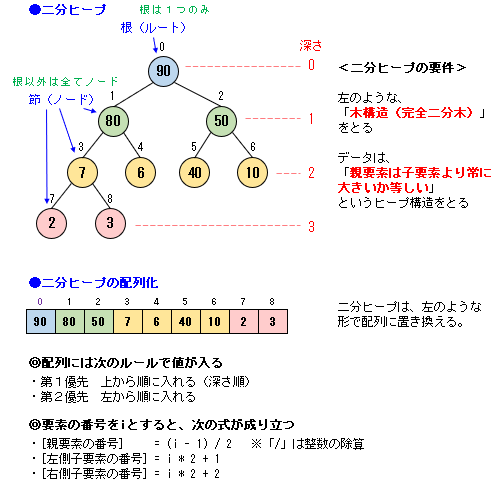
プログラムでは、この二分ヒープを、上の図ように配列に置き換えてコードを書くことになります。
配列の要素番号をiとすると、次の式が成り立ちます。

　[親要素の番号]     = (i - 1) / 2    ※/(スラッシュ)は整数の除算で小数点以下は切り捨て
　[左側子要素の番号] = i * 2 + 1
　[右側子要素の番号] = i * 2 + 2

1-1. ヒープソートのアルゴリズム概要

ヒープソートでは、最初に、配列を「二分ヒープ」の形にする必要があります。
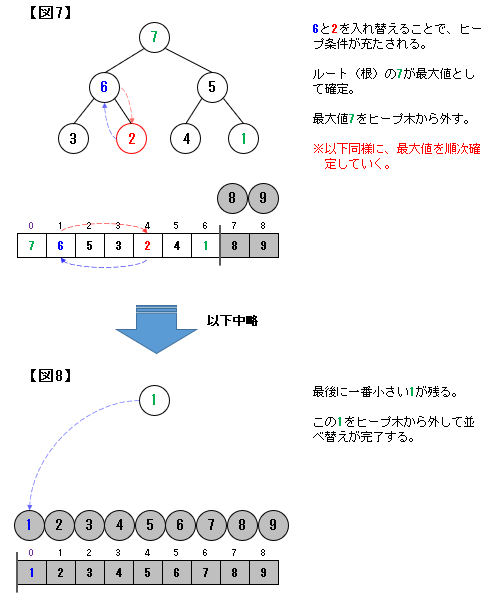
そして、二分ヒープの形を維持しながら、最大値である根（ルート）を順次取り出していくことになります。

アルゴリズムの考え方は、おおよそ「基本情報技術者試験平成30年度春期午後問8」に基づいています。
以下、順に見ていきます。

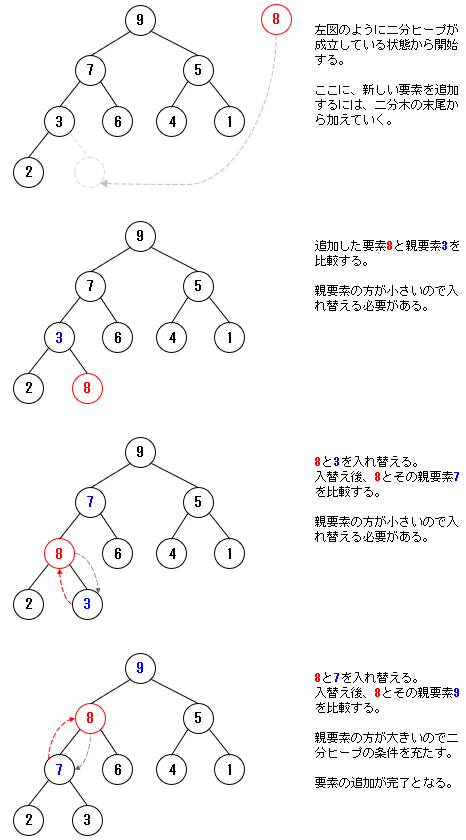
1-1-1. 配列を二分ヒープに変換する方法（up-heap）

ランダムな配列を二分ヒープにするためには、「既にヒープ構造になっている二分ヒープ木に対して、下から要素を追加していく方法」を使用します。
この方法は、アップヒープ（up-heap）といい、図で見ると次のような感じです。
赤色の⑧に注目すれば、上に移動（up）していくのが分かると思います。

アップヒープのイメージ

これを配列に当てはめると、次のような手順になります。

配列をヒープ構造に変換するイメージ

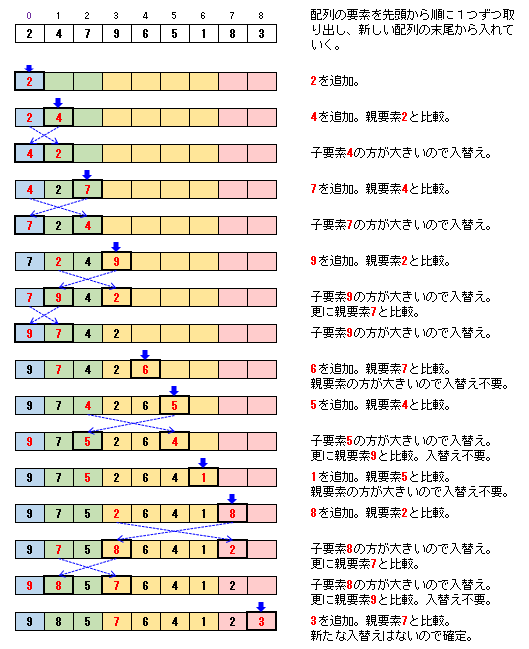
ここでは、わかりやすいように、元の配列から新しい配列に１つずつ要素を入れています。
しかし、図を見てわかるように、新しい配列を用意しなくとも、元の配列に要素を置いたまま、前から順にヒープ構造にしていくことができます。

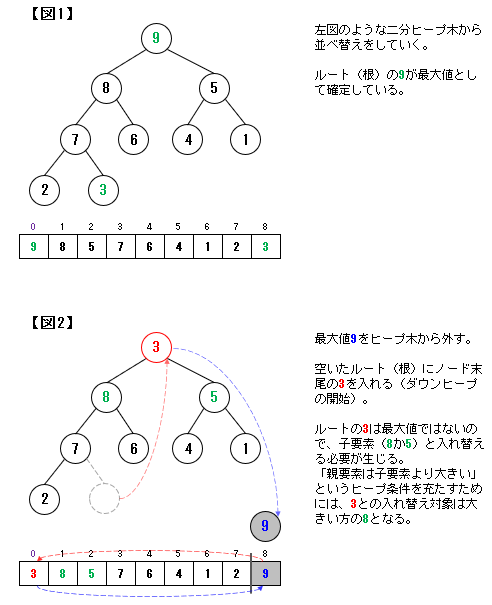
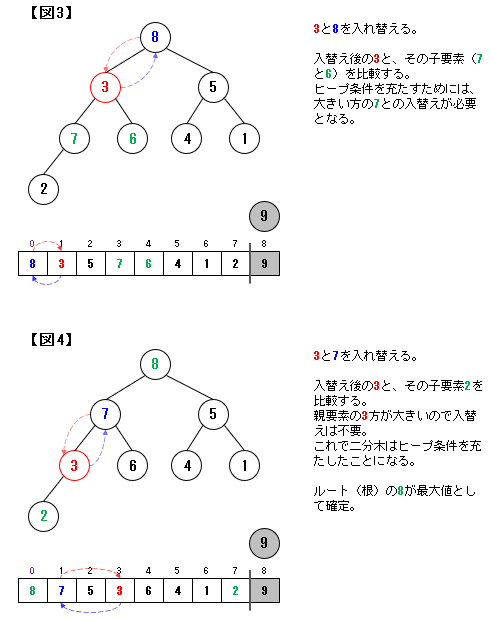
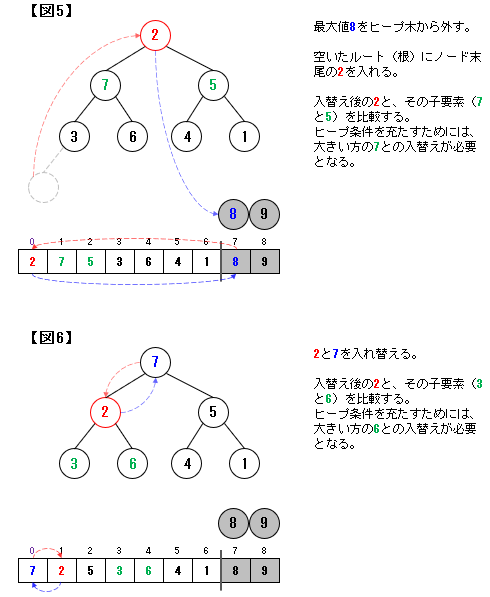
1-1-2. 二分ヒープから並べ替えをする方法（down-heap）

二分ヒープ木では根（ルート）が最大値となります。
この根（最大値）を取り出していくことで並べ替えを進めていくことになります（この点はバブルソートに近しい）。

なお、最大値を取り除くと、二分ヒープ構造が崩れます。
ここでは、下図のように上から要素を追加する形で二分ヒープ構造に戻していきます。
この方法をダウンヒープ（down-heap）といいます。
赤色の③に注目すれば、下に移動（down）していくのが分かると思います。

ダウンヒープによるソートのイメージ

動きとしては、バブルソートに近いと言えますが、ヒープソートの方が、比較数・交換数は少なくて済みますので、その分効率の良いアルゴリズムとなります。

また、ヒープソートは「元の配列に要素を置いたまま交換を繰り返すことにより並べ替えができるアルゴリズム」となります。
このようなソートアルゴリズムをIn-placeアルゴリズムといいます。In-placeアルゴリズムには、追加の記憶領域をほとんど使わないで済むという利点があります。

In-placeアルゴリズムの範疇に含まれるものには、クイックソート、バブルソートなどがあります。

1-2. ヒープソートのサンプルコード

1-2-1. C言語

＜ソースコード＞

heap_sort.c

#include <stdio.h>
#include <stdlib.h>  // malloc関数で使用
#include <time.h>  // time関数、clock関数で使用

int parent(int child) {return (child - 1) / 2;}  // 親要素の要素番号を取得
int left_child(int parent) {return parent * 2 + 1;}  // 左の子要素の要素番号を取得
int right_child(int parent) {return parent * 2 + 2;}  // 右の子要素の要素番号を取得
void swap(int *n1, int *n2);

// ヒープソート
void heap_sort(int *nums, int numslen) {
  // 配列を二分ヒープに変換する（up-heap）
  for (int i = 0; i < numslen; i++) {
    int j = i;  // 要素番号iにある要素を二分ヒープに追加（要素番号をjに代入）
    while (j > 0) {  // 要素番号が0以上の場合（子要素の番号である場合）はループを継続
      if (nums[j] > nums[parent(j)]) {  // 追加した要素が親要素より大きい場合
        swap(&nums[j], &nums[parent(j)]);  // 親要素と子要素を入れ替える
        j = parent(j);  // jの位置を入替え後の位置（親要素のあった位置）に移動
      } else {
        break;  // 親要素の方が大きければ入替えの必要がないので確定
      }
    }
  }

  // ソート処理（down-heap）
  for (int i = numslen - 1; i > 0; i--) {
    swap(&nums[0], &nums[i]);  // 根（ルート）の要素を最大値として確定して配列の後方に移動
    int j = 0;  // 配列の先頭に来た要素をdown-heapしていく

    while (left_child(j) < i) {
      // 子のうち値の大きい方の配列番号をtmpに格納
      int tmp = left_child(j);  // 一旦左の子の要素番号を入れる
      if (right_child(j) < i && nums[right_child(j)] > nums[tmp]) tmp = right_child(j);  // 右の要素（値）が大きければtmpを入替え

      // 親の値が子の値より小さければ入れ替え
      if (nums[j] < nums[tmp]) {
        swap(&nums[j], &nums[tmp]);
        j = tmp;
      } else {
        break;  // 親の値が子の値より大きければ確定
      }
    }
  }
}

// スワップ（入れ替え）関数
void swap(int *n1, int *n2) {
  int tmp = *n1;
  *n1 = *n2;
  *n2 = tmp;
}

// ヒープソートの実行
int main(void) {
  // ソート用の配列を作成
  srand((unsigned int)time(NULL)); // 乱数の発生をランダムにする
  int n = 10;
  int *nums = malloc(n * sizeof(int)); // int型配列のメモリを確保
  for (int i = 0; i < n; i++) nums[i] = (int)rand() % n; // ランダムな値を代入
  for (int i = 0; i < n; i++) printf("%d, ", nums[i]); // ソート前の配列出力
  printf("\n");

  heap_sort(nums, n);  

  for (int i = 0; i < n; i++) printf("%d, ", nums[i]); // ソート後の配列出力
  printf("\n");
  return 0;
}

＜出力確認＞

ターミナル

$ gcc heap_sort.c 
$ ./a.out 
4, 6, 9, 7, 4, 2, 8, 0, 3, 2, 
0, 2, 2, 3, 4, 4, 6, 7, 8, 9, 

1-2-2. Java

＜ソースコード＞

HeapSortTest.java

import java.util.Random;

public class HeapSortTest {
  public static void main(String[] args) {
    // ソート用の配列を作成
    int n = 10;
    int nums[] = new int[n];
    Random rand = new Random(); // 乱数のインスタンスを作成
    for (int i = 0; i < n; i++) nums[i] = rand.nextInt(n);  // ランダムな値を代入
    for (int i = 0; i < nums.length; i++) System.out.print(nums[i] + ", ");  // ソート前の配列出力
    System.out.print("\n");

    HeapSort(nums, n);  // ヒープソートの実行

    for (int i = 0; i < nums.length; i++) System.out.print(nums[i] + ", ");  // ソート前の配列出力
    System.out.print("\n");
  }

  public static void HeapSort(int nums[], int n) {
    // 配列を二分ヒープに変換する（up-heap）
    for (int i = 0; i < n; i++) {
      int j = i;  // 要素番号iにある要素を二分ヒープに追加（要素番号をjに代入）
      while (j > 0) {  // 要素番号が0以上の場合（子要素の番号である場合）はループを継続
        if (nums[j] > nums[parent(j)]) {  // 追加した要素が親要素より大きい場合
          Swap(nums, j, parent(j));  // 親要素と子要素を入れ替える
          j = parent(j);  // jの位置を入替え後の位置（親要素のあった位置）に移動
        } else {
          break;  // 親要素の方が大きければ入替えの必要がないので確定
        }
      }
    }

    // ソート処理（down-heap）
    for (int i = n - 1; i > 0; i--) {
      Swap(nums, 0, i);  // 根（ルート）の要素を最大値として確定して配列の後方に移動
      int j = 0;  // 配列の先頭に来た要素をdown-heapしていく

      while (left_child(j) < i) {
        // 子のうち値の大きい方の配列番号をtmpに格納
        int tmp = left_child(j);  // 一旦左の子の要素番号を入れる
        if (right_child(j) < i && nums[right_child(j)] > nums[tmp]) tmp = right_child(j);  // 右の要素（値）が大きければtmpを入替え

        // 親の値が子の値より小さければ入れ替え
        if (nums[j] < nums[tmp]) {
          Swap(nums, j, tmp);
          j = tmp;
        } else {
          break;  // 親の値が子の値より大きければ確定
        }
      }
    }    
  }

  public static int parent(int child) {return (child - 1) / 2;}  // 親要素の要素番号を取得
  public static int left_child(int parent) {return parent * 2 + 1;}  // 左の子要素の要素番号を取得
  public static int right_child(int parent) {return parent * 2 + 2;}  // 右の子要素の要素番号を取得

  public static void Swap(int nums[], int n1, int n2) {
    int tmp = nums[n1];
    nums[n1] = nums[n2];
    nums[n2] = tmp;
  }
}

＜出力確認＞

ターミナル

$ javac HeapSortTest.java
$ java HeapSortTest
2, 0, 4, 3, 3, 3, 3, 8, 9, 5, 
0, 2, 3, 3, 3, 3, 4, 5, 8, 9, 

1-2-3. VBA

＜ソースコード＞

'ヒープソート
Sub HeapSort(nums() As Long)
    Dim i As Long
    Dim c As Long '主に子(child)の要素番号に使用
    Dim p As Long '主に親(parent)の要素番号に使用

    '配列を二分ヒープに変換する（up-heap）
    For i = 0 To UBound(nums)
        c = i
        Do While c > 0
            If nums(c) <= nums(GetPNode(c)) Then Exit Do '子が親以下の値であればループを抜ける（VBAはOrでは結べない）
            Call Swap(nums(c), nums(GetPNode(c)))
            c = GetPNode(c)
        Loop
    Next

    'ソート処理（down-heap）
    For i = UBound(nums) To 0 Step -1
        p = 0
        Call Swap(nums(p), nums(i))
        Do While GetLNode(p) < i
            '子のうち値の大きい方の配列番号をcに格納
            If GetLNode(p) = i - 1 Then '子要素が左のみであれば
                c = GetLNode(p) 'cに左の子の要素番号を格納
            ElseIf nums(GetLNode(p)) > nums(GetRNode(p)) Then '左の要素の値が右の要素より大きければ（VBAはOrでは結べない）
                c = GetLNode(p) 'cに左の子の要素番号を格納
            Else
                c = GetRNode(p) 'cに右の子の要素番号を格納
            End If

            '親の値が子の値より小さければ入れ替え
            If nums(p) >= nums(c) Then Exit Do '親が子以上の値であればループを抜ける
            Call Swap(nums(p), nums(c))
            p = c
        Loop
    Next
End Sub

'親要素の要素番号を取得
Function GetPNode(n As Long) As Long
    GetPNode = (n - 1) \ 2
End Function

'左の子要素の要素番号を取得
Function GetLNode(n As Long) As Long
    GetLNode = n * 2 + 1
End Function

'右の子要素の要素番号を取得
Function GetRNode(n As Long) As Long
    GetRNode = n * 2 + 2
End Function

'スワップ
Sub Swap(a As Variant, b As Variant)
    Dim tmp As Variant
    tmp = a
    a = b
    b = tmp
End Sub

＜出力確認＞

ヒープソートの実行（VBA）

Sub OutputHeapSoat()
    Dim nums() As Long
    Call CreateArray(nums, 10) '配列を作成
    Call PrintArray(nums) 'ソート前の配列を出力

    Call HeapSort(nums)

    Call PrintArray(nums) 'ソート前の配列を出力
End Sub

乱数作成（VBA）

'乱数による配列作成プロシージャ
Sub CreateArray(nums() As Long, n As Long)
    Dim i As Long
    ReDim nums(n - 1)
    Randomize '乱数ジェネレーターを初期化（都度異なる乱数値を取得するため）
    For i = 0 To UBound(nums)
        nums(i) = Fix(Rnd * n)
    Next
End Sub

配列出力（VBA）

'1次元配列の内容を出力するプロシージャ
Sub PrintArray(nums As Variant)
    Dim i As Long
    Dim buf As String
    For i = 0 To UBound(nums)
        buf = buf & nums(i) & ", "
    Next
    Debug.Print buf
End Sub

イミディエイトウィンドウ（2行目がソート後の配列）

1, 1, 6, 6, 0, 6, 2, 8, 6, 9, 
0, 1, 1, 2, 6, 6, 6, 6, 8, 9, 

1-2-4. Python

＜ソースコード＞

HeapSort.py

import random

def parent(child): return (child - 1) // 2
def left_child(parent): return parent * 2 + 1
def right_child(parent): return parent * 2 + 2

# ヒープソート
def heap_sort(nums):
  for i in range(len(nums)):
    j = i
    while j > 0:
      if nums[j] > nums[parent(j)]: nums[j], nums[parent(j)], j = nums[parent(j)], nums[j], parent(j)
      else: break

  for i in range(len(nums) - 1, 0, -1):
    nums[0], nums[i], j = nums[i], nums[0], 0
    while left_child(j) < i:
      tmp = left_child(j)
      if right_child(j) < i and nums[right_child(j)] > nums[tmp]: tmp = right_child(j)
      if nums[j] < nums[tmp]: nums[j], nums[tmp], j = nums[tmp], nums[j], tmp
      else: break

# ヒープソートの実行
n = 10
nums = [random.randint(0, n - 1) for i in range(n)]
print(nums)  # ソート前の配列出力

heap_sort(nums)  # ヒープソート

print(nums)  # ソート後の配列出力

＜出力確認＞

ターミナル

> python HeapSort.py  
[0, 0, 8, 2, 3, 9, 4, 5, 0, 5]
[0, 0, 0, 2, 3, 4, 5, 5, 8, 9]

2. クイックソート

クイックソートは、その名のとおり処理速度が速いアルゴリズムです。

2-1. クイックソートのアルゴリズム概要

2-1-1. 基本となる考え方

クイックソートでは、以下の図のように、配列の中で基準となる数値を一つ決めて、基準よりも小さい値のグループと、基準以上の値のグループに分けていきます。
各グループで更にこれを繰り返すことで、並べ替えを完了させるアルゴリズムです。

クイックソートのイメージ

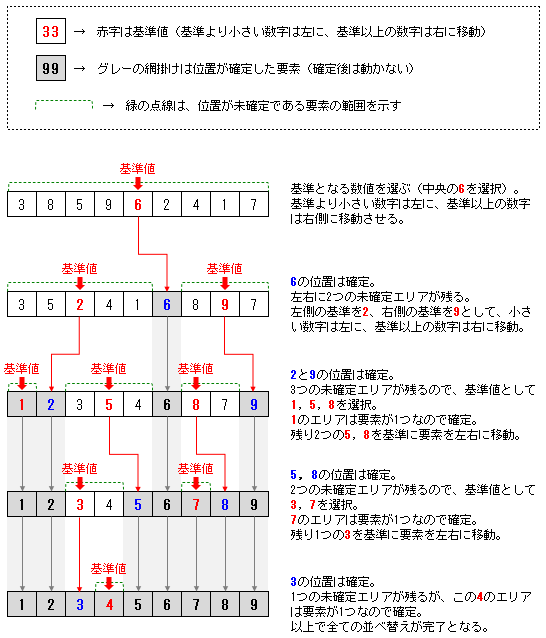
クイックソートもヒープソートと同様に、In-placeアルゴリズム（元の配列に要素を置いたまま交換により並べ替えをするアルゴリズム）の範疇に入ります。

2-1-2. 基準値との比較方法と要素の交換方法

クイックソートをコード化する一般的な考え方として「基本情報技術者試験平成27年度春期午後問8」があります（Wikipediaの解説も同様）が、この方法を採ると無限ループを回避する工夫が必要となるため結構面倒でした。

ここでは、こちらの論文「(MAX上における)アルゴリズム的問題におけるユーザーインターフェースの改良」で紹介されているクイックソートの考え方をベースとして次のような方法でコードを書いていきます。

クイックソートにおける要素交換方法のイメージ


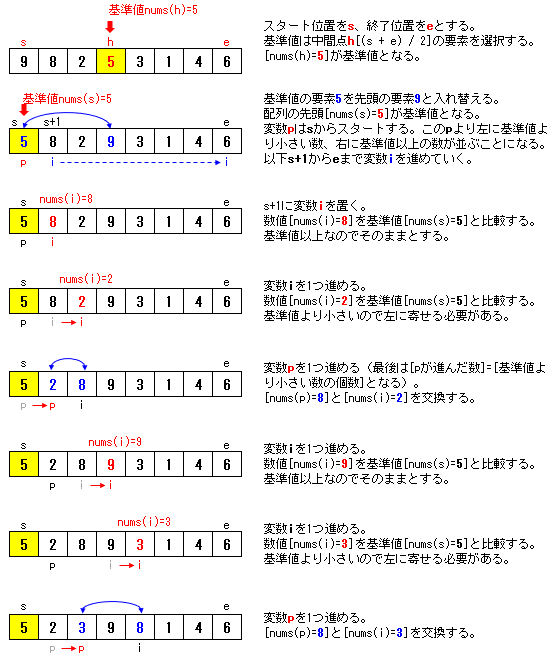
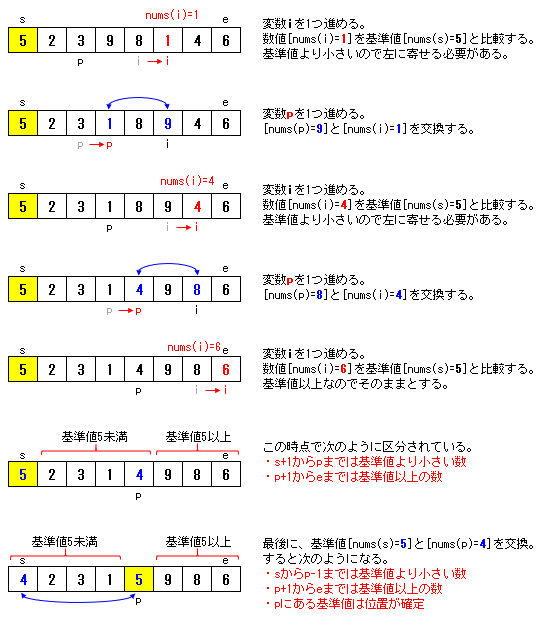
以上の処理を終えた後に、更に、基準値未満の数（sからp-1までの要素）と、基準値以上の数（p+1からeまでの要素）について同じ処理を再帰的に繰り返すことになります。

2-2. クイックソートのサンプルコード

2-2-1. C言語

＜ソースコード＞

quick_sort.c

#include <stdio.h>
#include <stdlib.h>  // malloc関数で使用
#include <time.h>  // time関数、clock関数で使用

void swap(int *n1, int *n2);

// クイックソート
void quick_sort(int *nums, int s, int e) {
  if (s >= e) return;  // 配列の要素数が1以下の場合は処理不要
  int p = s;  // 最終的にはこのpの位置より左側に基準値より小さい要素が並ぶ
  int h = (s + e) / 2;  // 基準値は配列中央から選ぶことにする
  swap(&nums[s], &nums[h]);  // 基準値は一旦配列先頭に置いておく（基準値=nums[s]となる）
  for (int i = s + 1; i <= e; i++) {
    if (nums[i] < nums[s]) swap(&nums[++p], &nums[i]);  // 基準値より小さい要素をpの左側に移動させていく
  }
  swap(&nums[s], &nums[p]);  // 基準値をpの位置に置き換える（基準値の位置が確定）
  quick_sort(nums, s, p - 1);  // 配列前半部分（基準値より小さい値）を再帰処理
  quick_sort(nums, p + 1, e);  // 配列後半部分（基準値以上の値）を再帰処理
}

// スワップ（入れ替え）関数
void swap(int *n1, int *n2) {
  int tmp = *n1;
  *n1 = *n2;
  *n2 = tmp;
}

// クイックソートの実行
int main(void) {
  // ソート用の配列を作成
  srand((unsigned int)time(NULL)); // 乱数の発生をランダムにする
  int n = 10;
  int *nums = malloc(n * sizeof(int)); // int型配列のメモリを確保
  for (int i = 0; i < n; i++) nums[i] = (int)rand() % n; // ランダムな値を代入
  for (int i = 0; i < n; i++) printf("%d, ", nums[i]); // ソート前の配列出力
  printf("\n");

  quick_sort(nums, 0, n - 1); // クイックソートの実行

  for (int i = 0; i < n; i++) printf("%d, ", nums[i]); // ソート後の配列出力
  printf("\n");
  return 0;
}

＜出力確認＞

ターミナル

$ gcc quick_sort.c 
$ ./a.out 
3, 8, 9, 5, 0, 9, 8, 1, 2, 8, 
0, 1, 2, 3, 5, 8, 8, 8, 9, 9, 

参考：先頭要素を基準値とした場合

なお、リスクはありますが、並べ替えする配列がランダムなものであれば、先頭の要素をそのまま基準値として、次のように簡潔に書くこともできます。
交換回数も減るので、スピードも少し早くなります（配列の並びがランダムであれば）。

quick_sort2.c

// クイックソート（先頭要素を基準値とした場合）
void quick_sort(int *nums, int s, int e) {
  if (s >= e) return;
  int p = s;
  for (int i = s + 1; i <= e; i++) if (nums[i] < nums[s]) swap(&nums[++p], &nums[i]);
  swap(&nums[s], &nums[p]);
  quick_sort(nums, s, p - 1);
  quick_sort(nums, p + 1, e);
}

でも、並べ替える配列が、もともと昇順に近い形である場合には、かなり無駄な演算を繰り返すことになりますので、やっぱりこの書き方はあまり適切でないと思います。

2-2-2. Java

＜ソースコード＞

QuickSortTest.java

import java.util.Random;

public class QuickSortTest {
  public static void main(String[] args) {
    // ソート用の配列を作成
    int n = 10;
    int nums[] = new int[n];
    Random rand = new Random(); // 乱数のインスタンスを作成
    for (int i = 0; i < n; i++) nums[i] = rand.nextInt(n);  // ランダムな値を代入
    for (int i = 0; i < nums.length; i++) System.out.print(nums[i] + ", ");  // ソート前の配列出力
    System.out.print("\n");

    QuickSort(nums, 0, n - 1);  // クイックソートの実行

    for (int i = 0; i < nums.length; i++) System.out.print(nums[i] + ", ");  // ソート前の配列出力
    System.out.print("\n");
  }

  // クイックソート
  public static void QuickSort(int nums[], int s, int e) {
    if (s >= e) return;  // 配列の要素数が1以下の場合は処理不要
    int p = s;  // 最終的にはこのpの位置より左側に基準値より小さい要素が並ぶ
    int h = (s + e) / 2;  // 基準値は配列中央から選ぶことにする
    Swap(nums, s, h);  // 基準値は一旦配列先頭に置いておく（基準値=nums[s]となる）
    for (int i = s + 1; i <= e; i++) {
      if (nums[i] < nums[s]) Swap(nums, ++p, i);  // 基準値より小さい要素をpの左側に移動させていく
    }
    Swap(nums, s, p);  // 基準値をpの位置に置き換える（基準値の位置が確定）
    QuickSort(nums, s, p - 1);  // 配列前半部分（基準値より小さい値）を再帰処理
    QuickSort(nums, p + 1, e);  // 配列後半部分（基準値以上の値）を再帰処理
  }

  // Swap関数
  public static void Swap(int nums[], int n1, int n2) {
    int tmp = nums[n1];
    nums[n1] = nums[n2];
    nums[n2] = tmp;
  }
}

＜出力確認＞

ターミナル

$ javac QuickSortTest.java 
$ java QuickSortTest
9, 9, 1, 3, 9, 0, 6, 7, 4, 7, 
0, 1, 3, 4, 6, 7, 7, 9, 9, 9,

2-2-3. VBA

＜ソースコード＞

'クイックソート
'引数（nums=対象となる配列、s=配列の開始位置、e=配列の終了位置）
Sub QuickSort(nums() As Long, s As Long, e As Long)
    If s >= e Then Exit Sub '開始位置sが終了位置e以降になる場合は関数を抜ける
    Dim i As Long
    Dim p As Long: p = s

    Call Swap(nums(s), nums((s + e) \ 2)) '配列中央の値を基準値にして先頭と入れ替え
    For i = s + 1 To e
        If nums(i) < nums(s) Then 'nums(s)を基準値として数値を比較していく
            p = p + 1 '基準値より小さい数があるごとにpを1つ進める
            Call Swap(nums(i), nums(p)) 'Swap関数で入れ替えを行う。
        End If
    Next
    Call Swap(nums(s), nums(p)) 'Swap関数で入れ替え

    Call QuickSort(nums, s, p - 1) '基準値より小さいグループを再帰処理
    Call QuickSort(nums, p + 1, e) '基準値より大きいグループを再帰処理
End Sub

'スワップ
Sub Swap(a As Variant, b As Variant)
    Dim tmp As Variant
    tmp = a
    a = b
    b = tmp
End Sub

＜出力確認＞

クイックソートの実行（VBA）

Sub OutputQuickSort()
    Dim nums() As Long
    Call CreateArray(nums, 10) '配列を作成
    Call PrintArray(nums) 'ソート前の配列を出力

    Call QuickSort(nums, 0, UBound(nums)) 'クイックソートを実行

    Call PrintArray(nums) 'ソート後の配列を出力
End Sub

※CreateArray関数と、PrintArray関数はヒープソートと同じものを使用しています。

イミディエイトウィンドウ（2行目がソート後の配列）

1, 8, 5, 3, 1, 9, 0, 3, 0, 5, 
0, 0, 1, 1, 3, 3, 5, 5, 8, 9, 

2-2-4. Python

＜ソースコード＞

QuickSort.py

import random

# クイックソート
def quick_sort(nums, s ,e):
  if s >= e: return
  p, h = s, (s + e) // 2
  nums[s], nums[h] = nums[h], nums[s]
  for i in range(s + 1, e + 1):
    if nums[i] < nums[s]:
      p += 1
      nums[p], nums[i] = nums[i], nums[p]
  nums[s], nums[p] = nums[p], nums[s]
  quick_sort(nums, s ,p - 1)
  quick_sort(nums, p + 1 ,e)

# クイックソートの実行
n = 10
nums = [random.randint(0, n - 1) for i in range(n)]
print(nums)  # ソート前の配列出力

quick_sort(nums, 0, n - 1)  # クイックソート

print(nums)  # ソート後の配列出力

＜出力確認＞

ターミナル

> python QuickSort.py 
[9, 2, 8, 7, 2, 3, 5, 4, 0, 7]
[0, 2, 2, 3, 4, 5, 7, 7, 8, 9]

3. マージソート

マージソートは、元の配列の並び方に影響を受けることがあまりなく、処理速度もクイックソート並みに早いです。
マージを行う際に、追加の記憶領域が必要となってしまいますが（in-placeではない = not-in-place）、無駄の少ない綺麗なアルゴリズムだと思います（個人的に）。

考え方と実装方法は、おおよそ「基本情報技術者試験平成22年度春期午後問8」に基づいています。

3-1. マージソートのアルゴリズム概要

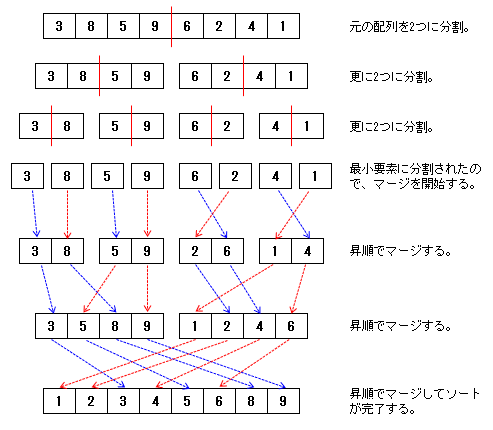
マージソートは、以下の図のように配列を最小単位まで分割した上で、昇順でマージを繰り返していくアルゴリズムです。

マージソートのイメージ

そして、マージ（並べ替え）をどうするかですが、昇順でマージを行う処理は次のような考え方で実装します。

マージ方法のイメージ

＜マージの実装方法＞
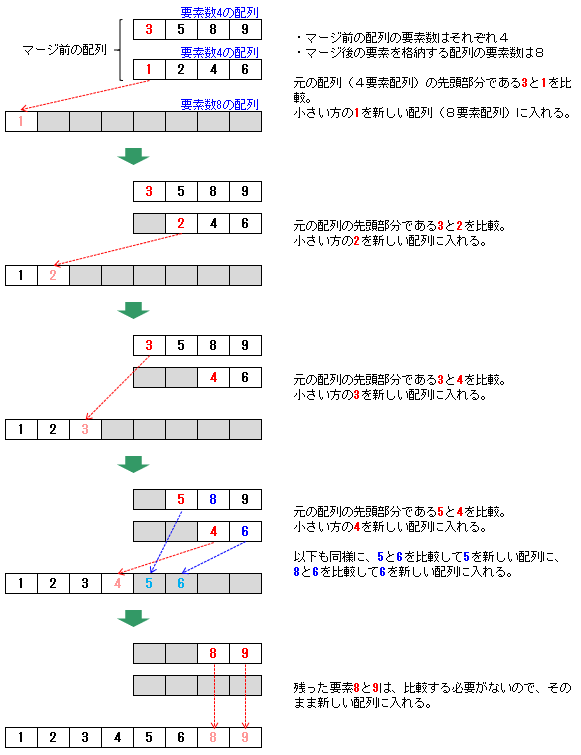
実際にコードを書く場合は、次の図のように、半分（後半部分）は元の配列に残したまま、もう半分（前半部分）のみを取り出した上でマージ処理を行っていくのが効率的です。

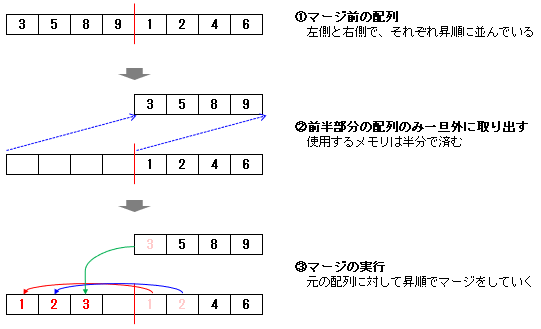
これにより、追加で使用するメモリの領域が半分で済み、メモリのコピーも半分で済みます。

＜前半部分と後半部分の値が同じ場合＞
なお、前半部分と後半部分の先頭部分の要素が、それぞれ同じ値の場合は、前半部分を優先してマージします。
そうすることで、「同等なデータのソート前の順序が、ソート後も保存される」こととなります（これを「安定ソート」と言います）。

3-2. マージソートのサンプルコード

3-2-1. C言語

＜ソースコード＞

merge_sort.c

#include <stdio.h>
#include <stdlib.h>  // malloc関数で使用
#include <time.h>  // time関数、clock関数で使用

// マージソート
void merge_sort(int *nums, int s, int e) {
  // 配列の分割位置を決める
  int h = (s + e) / 2;  // hは中央値
  int lenl = h - s + 1;  // lenlは前半部分の配列の要素数（わかりやすくするため変数に格納）
  int lenr = e - h;  // lenrは後半部分の配列の要素数（わかりやすくするため変数に格納）

  // 分割した配列が２以上の要素を持つときは再帰処理を行う（再帰処理の終了後は各配列が昇順になっている）
  if (lenl > 1) merge_sort(nums, s, h);
  if (lenr > 1) merge_sort(nums, h + 1, e);

  // 前半部分を新たな配列に格納
  int *tmpnums = malloc(lenl * sizeof(int));  // 分割した配列を格納するメモリを確保（gccでは int tmpnums[lenl]; でもOK）
  for (int i = 0; i < lenl; i++) tmpnums[i] = nums[s + i];

  // ２つの配列を昇順にマージ
  int nl = 0, nr = 0;
  for (int i = s; i <= e; i++) {
    if (nl > lenl - 1) break;  // 前半部分の要素が全てマージされた場合は全ての並べ替えが終了
    if (nr > lenr - 1 || tmpnums[nl] <= nums[h + 1 + nr]) {
      nums[i] = tmpnums[nl++];  // 後半部分の要素が全てマージ or [前半部分の要素]<=[後半部分の要素] の場合
    } else {
      nums[i] = nums[h + 1 + nr++];  // [前半部分の要素]>[後半部分の要素] の場合
    }
  }

  // メモリの解放
  free(tmpnums);
}

// マージソートの実行
int main(void) {
  // ソート用の配列を作成
  srand((unsigned int)time(NULL)); // 乱数の発生をランダムにする
  int n = 10;
  int *nums = malloc(n * sizeof(int)); // int型配列のメモリを確保
  for (int i = 0; i < n; i++) nums[i] = (int)rand() % n; // ランダムな値を代入
  for (int i = 0; i < n; i++) printf("%d, ", nums[i]); // ソート前の配列出力
  printf("\n");

  merge_sort(nums, 0, n - 1);  // マージソートの実行

  for (int i = 0; i < n; i++) printf("%d, ", nums[i]); // ソート後の配列出力
  printf("\n");
  return 0;
}

可読性優先で冗長な書き方をしているため、コードが長く見えます。
変数を減らして整理するとmerge_sort部分だけであれば10行くらいで済みます。

＜出力確認＞

ターミナル

$ gcc merge_sort.c 
$ ./a.out 
9, 4, 6, 9, 8, 5, 0, 5, 5, 3, 
0, 3, 4, 5, 5, 5, 6, 8, 9, 9, 

3-2-2. Java

＜ソースコード＞

MergeSortTest.java

import java.util.Random;

public class MergeSortTest {
  public static void main(String[] args) {
    // ソート用の配列を作成
    int n = 10;
    int nums[] = new int[n];
    Random rand = new Random(); // 乱数のインスタンスを作成
    for (int i = 0; i < n; i++) nums[i] = rand.nextInt(n);  // ランダムな値を代入
    for (int i = 0; i < nums.length; i++) System.out.print(nums[i] + ", ");  // ソート前の配列出力
    System.out.print("\n");

    MergeSort(nums, 0, n - 1);  // マージソートの実行

    for (int i = 0; i < nums.length; i++) System.out.print(nums[i] + ", ");  // ソート前の配列出力
    System.out.print("\n");
  }

  public static void MergeSort(int nums[], int s, int e) {
    // 配列の分割位置を決める
    int h = (s + e) / 2;  // hは中央値
    int lenl = h - s + 1;  // lenlは前半部分の配列の要素数（わかりやすくするため変数に格納）
    int lenr = e - h;  // lenrは後半部分の配列の要素数（わかりやすくするため変数に格納）

    // 分割した配列が２以上の要素を持つときは再帰処理を行う（再帰処理の終了後は各配列が昇順になっている）
    if (lenl > 1) MergeSort(nums, s, h);
    if (lenr > 1) MergeSort(nums, h + 1, e);

    // 前半部分を新たな配列に格納
    int tmpnums[] = new int[lenl];  // 分割した配列を格納する配列
    for (int i = 0; i < lenl; i++) tmpnums[i] = nums[s + i];

    // ２つの配列を昇順にマージ
    int nl = 0, nr = 0;
    for (int i = s; i <= e; i++) {
      if (nl > lenl - 1) break;  // 前半部分の要素が全てマージされた場合は全ての並べ替えが終了
      if (nr > lenr - 1 || tmpnums[nl] <= nums[h + 1 + nr]) {
        nums[i] = tmpnums[nl++];  // 後半部分の要素が全てマージ or [前半部分の要素]<=[後半部分の要素] の場合
      } else {
        nums[i] = nums[h + 1 + nr++];  // [前半部分の要素]>[後半部分の要素] の場合
      }
    }  
  }

  public static void Swap(int nums[], int n1, int n2) {
    int tmp = nums[n1];
    nums[n1] = nums[n2];
    nums[n2] = tmp;
  }
}

＜出力確認＞

ターミナル

$ javac MergeSortTest.java 
$ java MergeSortTest
3, 1, 6, 2, 3, 0, 7, 9, 3, 1, 
0, 1, 1, 2, 3, 3, 3, 6, 7, 9, 

3-2-3. VBA

＜ソースコード＞

マージソート（VBA）

Sub MergeSort(nums() As Long, s As Long, e As Long)
    Dim i As Long
    Dim h As Long: h = (s + e) \ 2
    Dim numsTmp() As Long: ReDim numsTmp(h - s)

    If h - s > 0 Then Call MergeSort(nums, s, h)
    If e - h - 1 > 0 Then Call MergeSort(nums, h + 1, e)
    For i = 0 To h - s
        numsTmp(i) = nums(s + i)
    Next

    Dim nl As Long: nl = 0
    Dim nr As Long: nr = 0
    For i = s To e
        If nl > h - s Then Exit For
        If nr > e - h - 1 Then
            nums(i) = numsTmp(nl)
            nl = nl + 1
        ElseIf numsTmp(nl) < nums(h + 1 + nr) Then
            nums(i) = numsTmp(nl)
            nl = nl + 1
        Else
            nums(i) = nums(h + 1 + nr)
            nr = nr + 1
        End If
    Next
End Sub

＜出力確認＞

マージソートの実行（VBA）

Sub OutputMergeSort()
    Dim nums() As Long
    Call CreateArray(nums, 10) '配列を作成
    Call PrintArray(nums) 'ソート前の配列を出力

    Call MergeSort(nums, 0, UBound(nums))

    Call PrintArray(nums) 'ソート後の配列を出力
End Sub

※CreateArray関数と、PrintArray関数はヒープソートと同じものを使用しています。

イミディエイトウィンドウ（2行目がソート後の配列）

1, 3, 9, 6, 5, 7, 2, 0, 8, 5, 
0, 1, 2, 3, 5, 5, 6, 7, 8, 9, 

3-2-4. Python

＜ソースコード＞

MergeSort.py

import random

# マージソート
def merge_sort(nums, s ,e):
  h = (s + e) // 2
  lenl, lenr = h - s + 1, e - h
  if lenl > 1: merge_sort(nums, s, h)
  if lenr > 1: merge_sort(nums, h + 1, e)
  tmp_nums = [nums[s + i] for i in range(lenl)]
  nl = nr = 0
  for i in range(s, e + 1):
    if nl > lenl - 1: break
    if nr > lenr - 1 or tmp_nums[nl] <= nums[h + 1 + nr]:
      nums[i] = tmp_nums[nl]
      nl += 1
    else:
      nums[i] = nums[h + 1 + nr]
      nr += 1

# マージソートの実行
n = 10
nums = [random.randint(0, n - 1) for i in range(n)]
print(nums)  # ソート前の配列出力

merge_sort(nums, 0, n - 1)  # マージソート

print(nums)  # ソート後の配列出力

＜出力確認＞

ターミナル

> python MergeSort.py 
[7, 8, 8, 1, 1, 4, 8, 2, 9, 2]
[1, 1, 2, 2, 4, 7, 8, 8, 8, 9]

4. バブルソート

バブルソートは処理速度が遅いですが、アルゴリズムが単純なので、簡単に作成することができます。
データが大量でなければ、バブルソートで十分なことも多いです。

4-1. バブルソートのアルゴリズム概要

バブルソートは、以下の図のように隣り合う要素を順に比較して、値が大きいものを後ろに移動させていくアルゴリズムです。
一巡するたびに、一番大きい値が末尾に置かれて確定していきます。
バブル（泡）がどんどん上に上っていくように、大きい値が末尾に移動して確定していくというイメージです。

バブルソートのイメージ

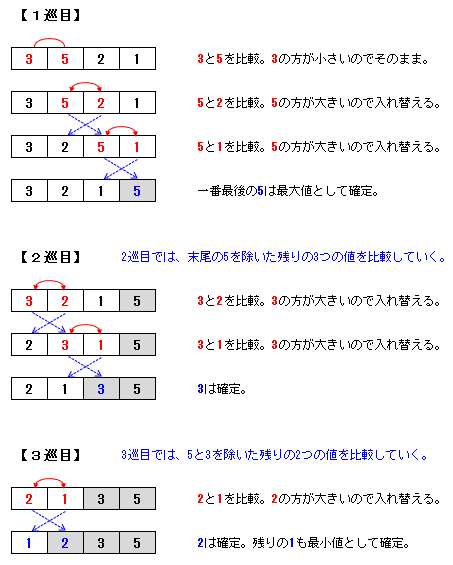
バブルソートもIn-placeアルゴリズム（元の配列に要素を置いたまま交換により並べ替えをするアルゴリズム）となります。

4-2. バブルソートのサンプルコード

4-2-1. C言語

bubble_sort関数自体は正味3行程度です。

＜ソースコード＞

bubble_sort.c

#include <stdio.h>
#include <stdlib.h>  // malloc関数で使用
#include <time.h>  // time関数、clock関数で使用

void swap(int *n1, int *n2);

// バブルソート
void bubble_sort(int *nums, int numslen) {
  for (int i = numslen - 1; i > 0; i--) {
    for (int j = 0; j < i; j++) {
      if (nums[j] > nums[j + 1]) swap(&nums[j], &nums[j + 1]);
    }
  }
}

// スワップ（入れ替え）関数
void swap(int *n1, int *n2) {
  int tmp = *n1;
  *n1 = *n2;
  *n2 = tmp;
}

// バブルソートの実行
int main(void) {
  // ソート用の配列を作成
  srand((unsigned int)time(NULL)); // 乱数の発生をランダムにする
  int n = 10;
  int *nums = malloc(n * sizeof(int)); // int型配列のメモリを確保
  for (int i = 0; i < n; i++) nums[i] = (int)rand() % n; // ランダムな値を代入
  for (int i = 0; i < n; i++) printf("%d, ", nums[i]); // ソート前の配列出力
  printf("\n");

  bubble_sort(nums, n);  // バブルソートの実行

  for (int i = 0; i < n; i++) printf("%d, ", nums[i]); // ソート後の配列出力
  printf("\n");
  return 0;
}

＜出力確認＞

ターミナル

$ gcc bubble_sort.c 
$ ./a.out 
8, 5, 6, 3, 1, 0, 5, 2, 2, 1, 
0, 1, 1, 2, 2, 3, 5, 5, 6, 8, 

4-2-2. Java

＜ソースコード＞

BubbleSortTest.java

import java.util.Random;

public class BubbleSortTest {
  public static void main(String[] args) {
    // ソート用の配列を作成
    int n = 10;
    int nums[] = new int[n];
    Random rand = new Random(); // 乱数のインスタンスを作成
    for (int i = 0; i < n; i++) nums[i] = rand.nextInt(n);  // ランダムな値を代入
    for (int i = 0; i < nums.length; i++) System.out.print(nums[i] + ", ");  // ソート前の配列出力
    System.out.print("\n");

    BubbleSort(nums);  // バブルソートの実行

    for (int i = 0; i < nums.length; i++) System.out.print(nums[i] + ", ");  // ソート前の配列出力
    System.out.print("\n");
  }

  // バブルソート
  public static void BubbleSort(int nums[]) {
    for (int i = nums.length - 1; i >= 0; i--) {
      for (int j = 0; j < i; j++) {
        if (nums[j] > nums[j + 1])  Swap(nums, j, j + 1);
      }
    }
  }

  public static void Swap(int nums[], int n1, int n2) {
    int tmp = nums[n1];
    nums[n1] = nums[n2];
    nums[n2] = tmp;
  }
}

＜出力確認＞

ターミナル

$ javac BubbleSortTest.java
$ java BubbleSortTest
2, 5, 9, 9, 1, 9, 2, 4, 0, 1, 
0, 1, 1, 2, 2, 4, 5, 9, 9, 9, 

4-2-3. VBA

＜ソースコード＞

バブルソート（VBA）

'バブルソート
Sub BubbleSort(nums() As Long)
    Dim i As Long
    Dim j As Long
    For i = UBound(nums) - 1 To 0 Step -1 '比較する範囲を1つずつ小さくしていく
        For j = 0 To i
            If nums(j) > nums(j + 1) Then
                Call Swap(nums(j), nums(j + 1)) '前方の値の方が大きければ数値を入れ替える
            End If
        Next
    Next
End Sub

スワップ関数（VBA）

'スワップ関数（値aと値bを入替えるプローシージャ）
Sub Swap(a As Variant, b As Variant)
    Dim tmp As Variant
    tmp = a
    a = b
    b = tmp
End Sub

＜出力確認＞

バブルソートの実行（VBA）

'BubbleSortの出力
Sub OutputBubbleSort()
    Dim nums() As Long
    Call CreateArray(nums, 10) '配列を作成
    Call PrintArray(nums) 'ソート前の配列を出力

    Call BubbleSort(nums) 'バブルソートを実行

    Call PrintArray(nums) 'ソート後の配列を出力
End Sub

※CreateArray関数と、PrintArray関数はヒープソートと同じものを使用しています。

イミディエイトウィンドウ（2行目がソート後の配列）

7, 2, 0, 9, 8, 8, 7, 6, 4, 2, 
0, 2, 2, 4, 6, 7, 7, 8, 8, 9, 

4-2-4. Python

＜ソースコード＞

BubbleSort.py

import random

# バブルソート
def bubble_sort(nums):
  for i in reversed(range(len(nums))):
    for j in range(i):
      if nums[j] > nums[j + 1]: nums[j], nums[j + 1] = nums[j + 1], nums[j]

# バブルソートの実行
n = 10
nums = [random.randint(0, n - 1) for i in range(n)]
print(nums)  # ソート前の配列出力

bubble_sort(nums)  # バブルソート

print(nums)  # ソート後の配列出力

＜出力確認＞

ターミナル

> python BubbleSort.py
[4, 3, 1, 4, 6, 8, 9, 6, 5, 0]
[0, 1, 3, 4, 4, 5, 6, 6, 8, 9]

5. 速度比較

最後に、各ソートアルゴリズムごと、各言語ごとに、処理速度の比較をしておきます。

実測結果は、教科書どおりにコンパイラ言語（C言語、Java）の方が速く、インタプリタ言語（VBA、Python）は10倍ほどの処理速度がかかるという結果になりました。
しかし、Pythonには奥の手（固有のSortメソッド）があり、コンパイラ言語並みのスピードを出すこともできます。

＜実測結果概要＞
要素数：100,000（配列の並びはランダム）
環境：Windows10（VBAがあるので、Windowsで比較しています。）
単位：秒（10回計測した平均値）

言語	ヒープソート	クイックソート	マージソート	バブルソート	固有メソッド
C言語	0.029	0.015	0.024	31.14	-
Java	0.022	0.018	0.029	16.092	0.021
VBA	0.904	0.244	0.161	528.979	-
Python	1.204	0.252	0.487	710.887	0.017

ソートアルゴリズム別に見ると、クイックソートが一番速いです。
配列の並びに左右されず安定的なスピードが出るのは、マージソートとヒープソートになります。

5-1. 計算量

本記事で取り上げた４つのソートアルゴリズムの計算量は次のとおりとなります（詳しくはこちらを参照）。

ソート種別	平均計算量	最大計算量	安定ソート
ヒープソート	O(nlog n)	O(nlog n)	×
クイックソート	O(nlog n)	O(n2)	×
マージソート	O(nlog n)	O(nlog n)	○
バブルソート	O(n2)	O(n2)	○

バブルソートの計算量は、要素数nの２乗に比例するので、大きな配列に使用するのは無理が生じます。
クイックソートは、基準値の選定を誤るとバブルソート並みに時間が掛かるので要注意です。

5-2. 処理速度の計測結果

5-2-1. C言語

当然ですが、C言語は比較的処理速度が速いです。
ランダムな分布であれば、クイックソートが一番処理時間が短くて済みました。

＜速度計測結果＞
要素数：100,000（配列の並びはランダム）
環境：Windows10
単位：秒

試行	ヒープソート	クイックソート	マージソート	バブルソート
1	0.028	0.016	0.022	31.157
2	0.027	0.015	0.024	31.458
3	0.029	0.015	0.024	31.537
4	0.029	0.016	0.024	30.812
5	0.03	0.015	0.023	30.975
6	0.028	0.015	0.024	31.111
7	0.028	0.015	0.024	31.236
8	0.028	0.015	0.023	30.99
9	0.029	0.015	0.024	31.219
10	0.029	0.015	0.025	30.903
平均	0.029	0.015	0.024	31.14

5-2-2. Java

Javaも処理速度がかなり速いです。
ヒープソートとバブルソートにおいては、C言語よりも短時間で処理が終わっています（なぜかは分かりません…）。

なお、Javaには、あらかじめソートメソッドがいくつか用意されています（詳しくは、Javaのソートの方法を一通り確認できるページを参照してください）。
ここでは、一般的と思われる、java.util.Arraysのsort()メソッドの処理速度も合わせて比較しておきます（次のソースコードを使用）。

JavaSortTest.java

import java.util.Random;
import java.math.BigDecimal;

public class JavaSortTest {
  public static void main(String[] args) {
    int n = 100000;
    int nums[] = new int[n];
    Random rand = new Random();
    for (int i = 0; i < n; i++) nums[i] = rand.nextInt(n);
    long start = System.nanoTime(); // スタート時間を記録

    java.util.Arrays.sort(nums);  // ソートの実行

    double processing_time = (System.nanoTime() - start) / Math.pow(10, 9);
    System.out.println(BigDecimal.valueOf(processing_time).toPlainString());  // 処理時間を出力
  }
}

＜速度計測結果＞
要素数：100,000（配列の並びはランダム）
環境：Windows10
単位：秒

試行	ヒープソート	クイックソート	マージソート	バブルソート	sort()メソッド
1	0.023	0.015	0.031	16.199	0.013
2	0.023	0.014	0.03	16.125	0.013
3	0.024	0.021	0.027	16.15	0.029
4	0.021	0.017	0.03	16.058	0.037
5	0.019	0.022	0.031	15.88	0.037
6	0.021	0.016	0.03	16.174	0.013
7	0.021	0.016	0.027	16.329	0.021
8	0.02	0.028	0.027	15.894	0.013
9	0.021	0.016	0.027	16.084	0.016
10	0.023	0.015	0.028	16.028	0.014
平均	0.022	0.018	0.029	16.092	0.021

5-2-3. VBA

VBAだと、CやJavaと比べると10倍くらいの時間が掛かっているようです。
特徴は、マージソートの方がクイックソートより速いことです。他の言語と異なる理由は分かりません。

バブルソートは、10万要素だと10分近く掛かるので、もうほとんどまともに動きません。
100万要素だと、単純に15時間ぐらいくらい掛かることになります。

＜速度計測結果＞
要素数：100,000（配列の並びはランダム）
環境：Windows10
単位：秒

試行	ヒープソート	クイックソート	マージソート	バブルソート
1	0.875	0.23	0.188	520.281
2	0.922	0.227	0.188	590.551
3	0.953	0.266	0.156	587.059
4	0.895	0.266	0.172	545.402
5	0.887	0.234	0.156	503.906
6	0.891	0.219	0.125	538.902
7	0.875	0.266	0.156	497.254
8	0.859	0.219	0.141	514.914
9	1	0.234	0.156	499.352
10	0.887	0.281	0.172	492.168
平均	0.904	0.244	0.161	528.979

5-2-4. Python

Pythonは、私の拙いコードの書き方が原因かもしれませんが、VBA並みもしくはそれ以上の処理時間が掛かっています。

ただし、Pythonには次のようなsortメソッドが用意されています。
これも同条件で速度を計測しましたが、C言語やJava並みの速度が出ています。この辺もPythonの良いところですね。

PythonSort.py

import random
import time  # timeモジュールをインポート

# ソートの実行
n = 100000
nums = [random.randint(0, n - 1) for i in range(n)]
start = time.time()  # スタート時間を記録

nums.sort()  # ソート

processing_time = time.time() - start
print(processing_time)  # 処理時間を出力

＜速度計測結果＞
要素数：100,000（配列の並びはランダム）
環境：Windows10
単位：秒

試行	ヒープソート	クイックソート	マージソート	バブルソート	Sortメソッド
1	1.001	0.218	0.5	710.887	0.015
2	1.011	0.227	0.493	-	0.016
3	1.284	0.37	0.476	-	0.017
4	1.352	0.237	0.484	-	0.018
5	1.043	0.232	0.476	-	0.019
6	1.018	0.236	0.48	-	0.016
7	1.523	0.23	0.484	-	0.017
8	1.367	0.312	0.493	-	0.017
9	1.049	0.215	0.506	-	0.017
10	1.386	0.235	0.482	-	0.017
平均	1.204	0.252	0.487	710.887	0.017

※バブルソートは、とんでもなく遅いので、1回だけしか実行していません。

5-3. 【参考】処理時間計測のソースコード

参考までに、処理時間を計測したソースコードも残しておきます。
ソートアルゴリズムのコードは省略しています。

5-3-1. Python

quick_sort.c

#include <stdio.h>
#include <stdlib.h>  // malloc関数で使用
#include <time.h>  // time関数、clock関数で使用

void quick_sort(int *nums, int s, int e);

// 中略

// クイックソートの実行
int main(void) {
  srand((unsigned int)time(NULL));
  int n = 100000;
  int *nums = malloc(n * sizeof(int));
  for (int i = 0; i < n; i++) nums[i] = (int)rand() % n;
  int start = clock(); // スタート時間を記録

  quick_sort(nums, 0, n - 1); // クイックソートの実行

  int end = clock();
  double processing_time = (double)(end - start) / CLOCKS_PER_SEC;
  printf("%f\n", processing_time);  // 処理時間を出力
  return 0;
}

5-3-2. Java

QuickSortTest.java

import java.util.Random;
import java.math.BigDecimal;

public class QuickSortTest {
  public static void main(String[] args) {
    int n = 100000;
    int nums[] = new int[n];
    Random rand = new Random();
    for (int i = 0; i < n; i++) nums[i] = rand.nextInt(n);
    long start = System.nanoTime(); // スタート時間を記録

    QuickSort(nums, 0, n - 1);  // クイックソートの実行

    double processing_time = (System.nanoTime() - start) / Math.pow(10, 9);
    System.out.println(BigDecimal.valueOf(processing_time).toPlainString());  // 処理時間を出力
}

  public static void QuickSort(int nums[], int s, int e) {
    // 中略
  }
}

5-3-3. VBA

Sub SortSpeed()
    Dim n As Long: n = 100000
    Dim nums() As Long
    Call CreateArray(nums, n) '配列を作成
    Dim startTime As Double: startTime = Timer 'スタート時間を記録

    Call QuickSort(nums, 0, UBound(nums)) 'クイックソート

    Dim processingTime As Double: processingTime = Timer - startTime
    Debug.Print processingTime
End Sub

5-3-4. Python

QuickSort.py

import random
import time  # timeモジュールをインポート

# クイックソート
def quick_sort(nums, s ,e):
  # 中略

# クイックソートの実行
n = 100000
nums = [random.randint(0, n - 1) for i in range(n)]
start = time.time()  # スタート時間を記録

quick_sort(nums, 0, n - 1)  # クイックソート

processing_time = time.time() - start
print(processing_time)  # 処理時間を出力

さいごに

図表に時間を取られて途中で先が見えなくなりましたが、何とか最後まで書けたので、まあ良しとします。
Pythonは使いこなせると便利だろうと思いますので、もう少し学習を進めていきたいところです。