概要
Mind で Neural Network (準備編1) 文字画像の読み込み の続きです。
実装を行うにあたり、ニューラルネットワークの 順伝播と逆伝播の処理内容を 図を作りながら調べました。
図に簡単な説明をつけて本記事として公開します。
背景
Deep Learning についての勉強をはじめました。
基本の ニューラルネットワークを 実装できる程度に理解することを 第一の目標としてます。
参考図書として
を用いてます。
この参考書では Python で numpy を用いて 行列で ニューラルネットワークの順伝播と逆伝播の処理を実装しています。
行列演算のない言語での実装では、参考図書の行列演算を、ループでの処理に展開を要します。
ループ内の個々の処理が、ニューラルネットワーク内でのどういう動きを示すのかを、図にしながら 理解していきました。
私と同様に ニューラルネットワークの処理内容を学ぶ方の 参考になれば幸いです。
本記事では 実装に必要となる式 を結果を中心に示しています。式の算出過程は、参考図書および他の記事に譲ります。
ニューラルネットワーク内の動き
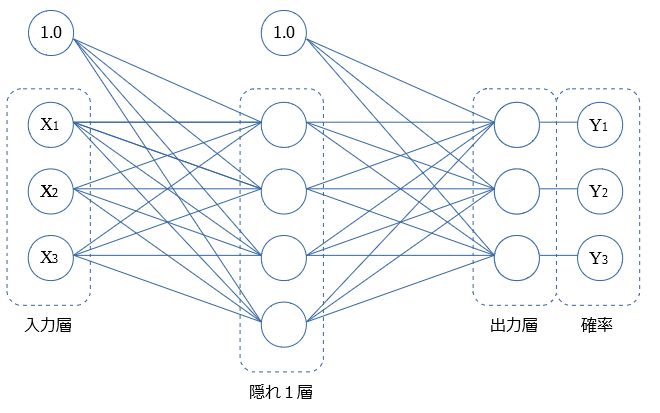
隠れ層が1つの構成で示していきます。
図中ではパーセプトロンを〇で示しています。本記事ではパーセプトロンを"〇"の記号で略します。
入力層は 画像などのデータの格納を行います。
$X_1$~$X_3$で示す〇は、画像の例では 画素(1点)の輝度値に対応します。
ニューラルネットワーク内を、
入力層 → 隠れ1層 → 出力層 → 確率
と伝播してき、判別結果が各確率 $Y_1$~$Y_3$ と算出されます。
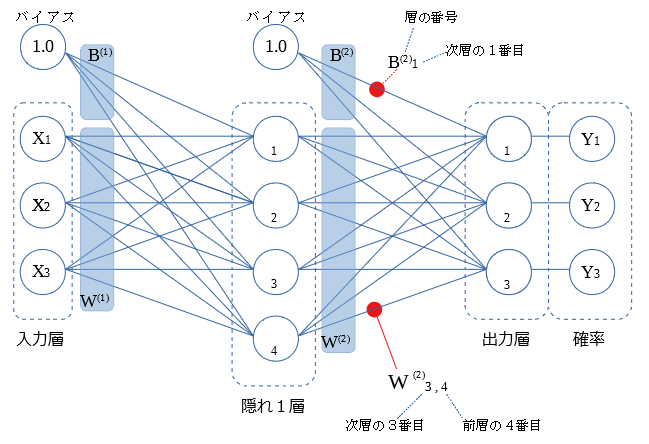
重み
前層から次層への値の伝達は 重み をかけて行います。
図にて $B^{(1)} B^{(2)} W^{(1)} W^{(2)}$ で示しす領域が 重み を示しています。
〇間の結線は 個々に異なる 重み をもちます。
個々の 重み に説明用に番号を付与します。(図中の赤線で例示)
この 重み の適切な値を求めることが ニューラルネットの学習 になります。
X → Y の流れを 順伝播と呼称します。
入力値からニューラルネットワークを介し判別結果の各確率を算出します。
X ← Y の流れを 逆伝播と呼称します。
正解(教師データ)と判別結果を比較し 誤差を求め、
重みの値を調整し誤差を小さくするために、
誤差を X←Yの方向に伝播させ、重みの微分値を算出します。
順伝播と逆伝播を図示していきます。
ReLU関数
本記事では ReLU関数を活性化関数に用います。
ReLU関数は、0以下の入力は0とし、0より大きい値はそのまま値を用いる関数です。
式を示します。
ReLU(x) = \left\{
\begin{array}{ll}
x & (0 \lt x) \\
0 & (x \leqq 0)
\end{array}
\right.
順伝播
入力層 → 隠れ1層
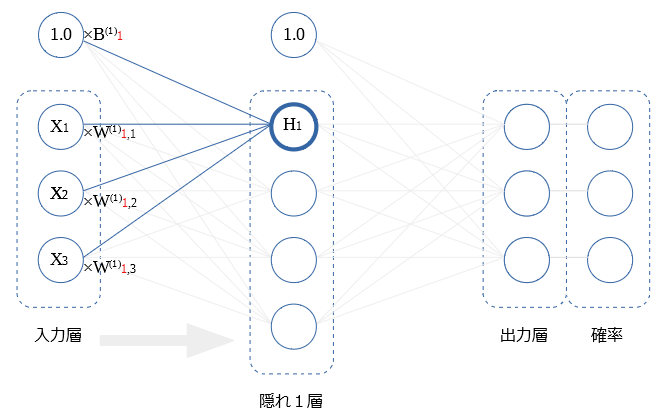
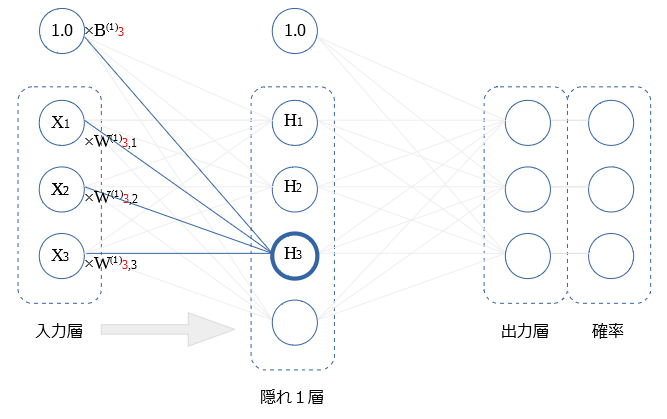
図の $H_1$に注目します。
$H_1$値は、バイアスと 前層の全$X$ から受けた値を、足し合わせ、活性化関数を行った値です。
式を示します。
$$H_1= ReLU( B_1^{(1)} + X_1W_{1,1}^{(1)} + X_2W_{1,2}^{(1)}+ X_3W_{1,3}^{(1)} )$$
$$ = ReLU( B_1^{(1)} + \sum_i X_iW_{1,i}^{(1)})$$
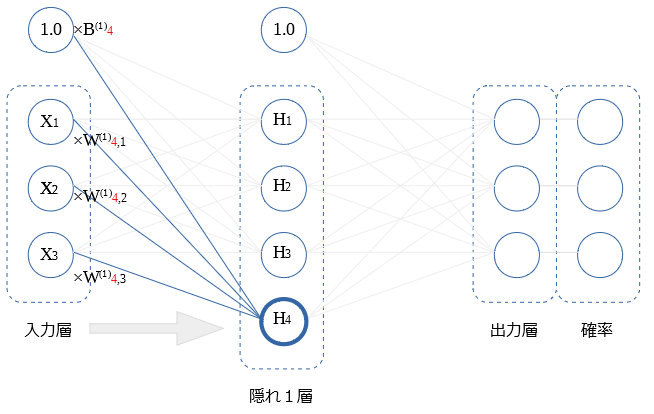
隠れ1層内の他の〇の値についても同様です。
$H_2$ ~ $H_4$ を図示します。
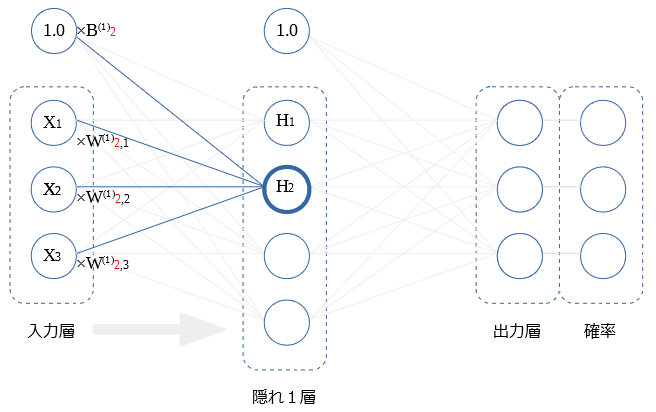
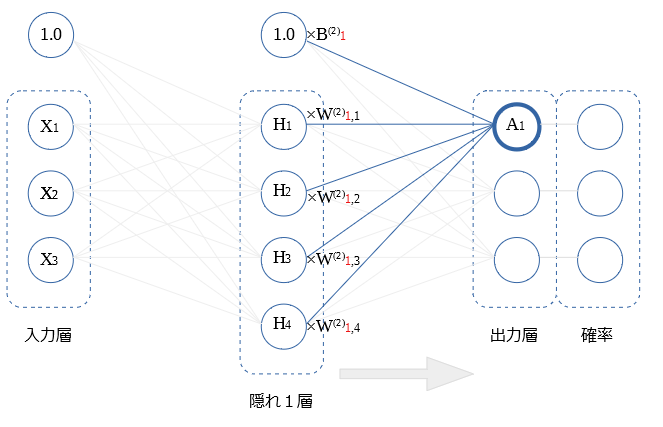
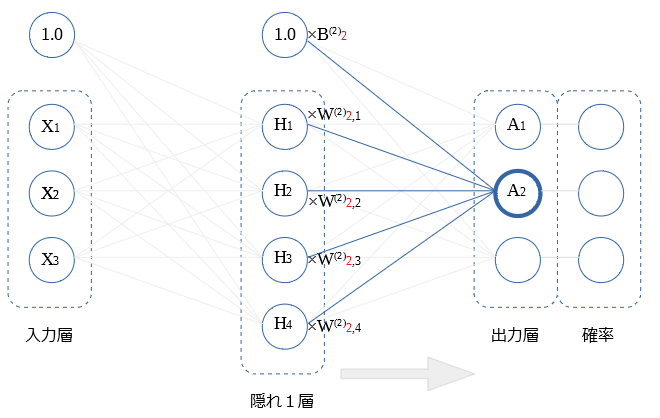
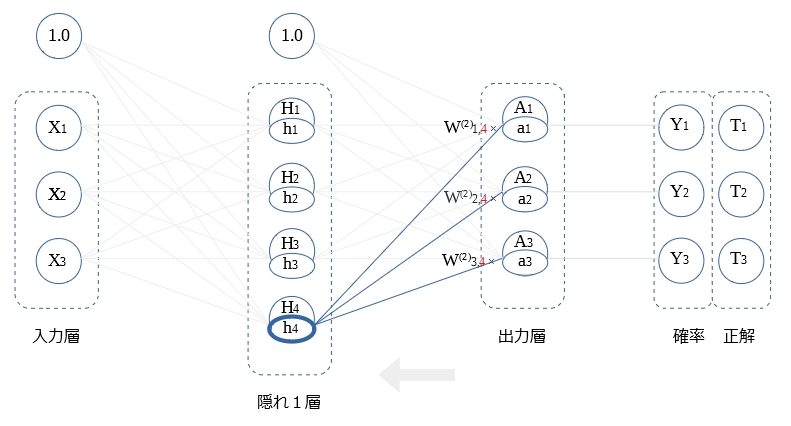
隠れ1層 → 出力層
出力層への伝達では、バイアスと 前層の全$H$ から受けた値を、足し合わせた値を用います。
活性化関数は用いません。
図の $A_1$の式を示します。
$$A_1= B_1^{(2)} + H_1W_{1,1}^{(2)} + H_2W_{1,2}^{(2)}+ H_3W_{1,3}^{(2)}+ H_4W_{1,4}^{(2)} $$
$$ = B_1^{(2)} + \sum_i H_iW_{1,i}^{(2)}$$
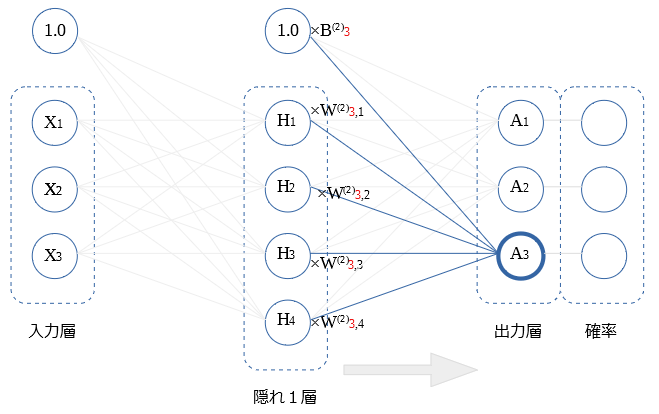
$A_2$、 $A_3$ も $A_1$と同様です、図示します。
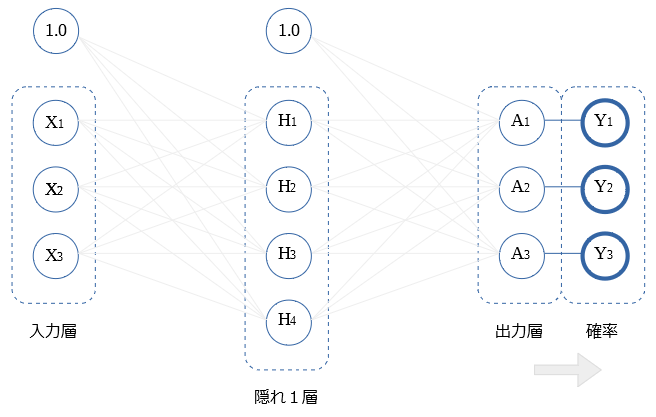
出力層 → 確率
出力層の〇の値を全て使用し Softmax関数にて 確率$Y$を算出します。
式を示します。
{ Y_i=\text{softmax}(A_i) = \frac{\exp(A_i)}{\exp(A_1)+\exp(A_2)+\exp(A_3)}}
{= \frac{\exp(A_i)}{\sum_j \exp(A_j)}}
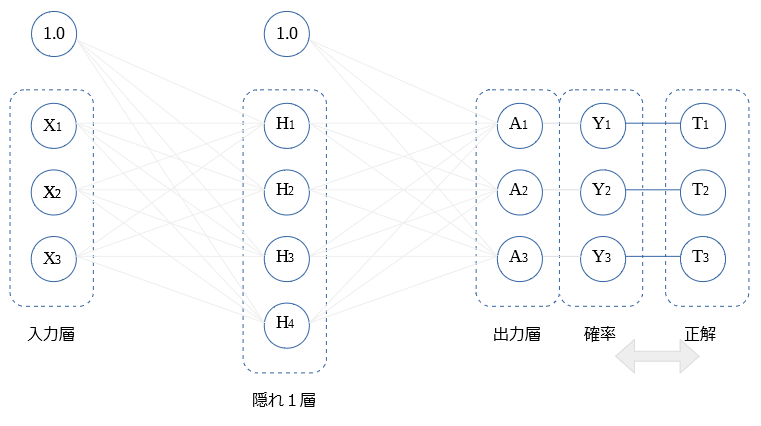
確率と正解の比較 誤差の算出
算出した確率$Y$と 正解値$T$を比較し、誤差を算出します。
正解値$T$は、正解の〇には 1.0 が格納され、他の〇には 0 が格納されてます。
($T_1$が正解の場合の例: $T_1$:1.0 , $T_2$:0 , $T_3$:0)
本記事では「交差エントロピー誤差」を用います。
式を示します。
$$E=-(T_1\log Y_1+T_2\log Y_2+T_3\log Y_3)$$
$$ =-\sum_i T_i\log Y_i$$
この値が小さくなるように 重み を調節するために、逆伝播を行っていき、重みの微分値を求めていきます。
逆伝播
順伝播で算出した値は 大文字 を用いてます。
対応する逆伝播値を 小文字 で示します。
出力層 ← 確率
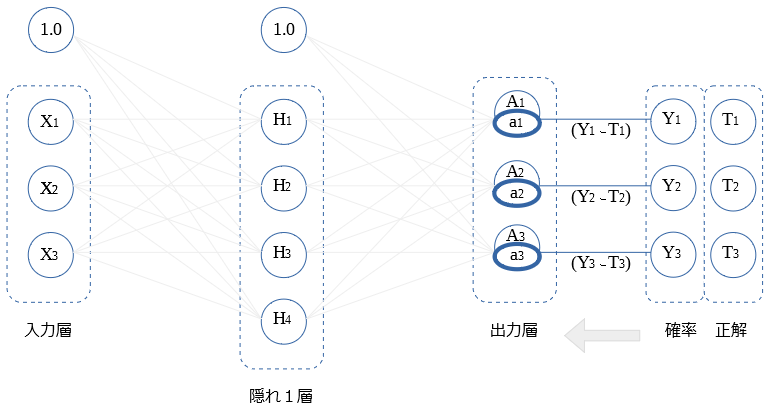
出力層の逆伝播値 $a$ の式を示します。
$$a_i = Y_i - T_i$$
この式が単純化するよう、softmax関数 と 交差エントロピー誤差 の組み合わせで設計されてます。(すばらしい)
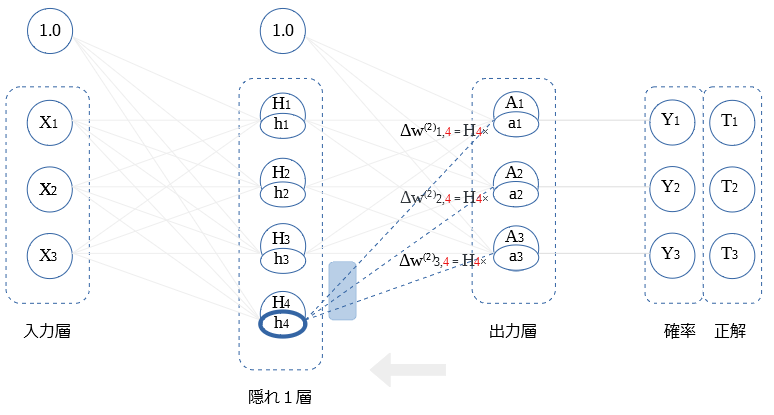
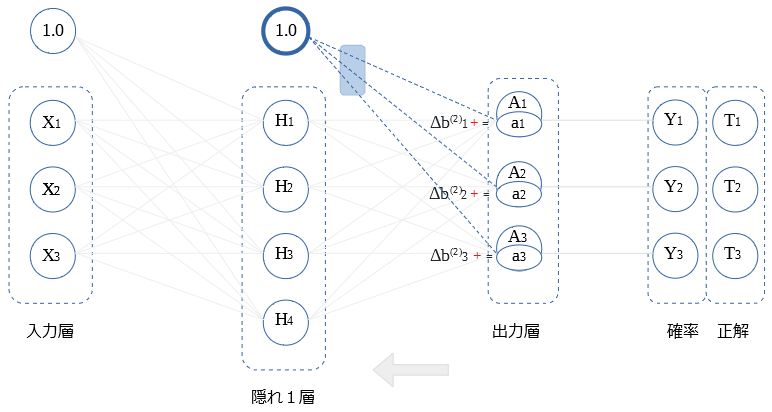
隠れ1層 ← 出力層 (重み微分値)
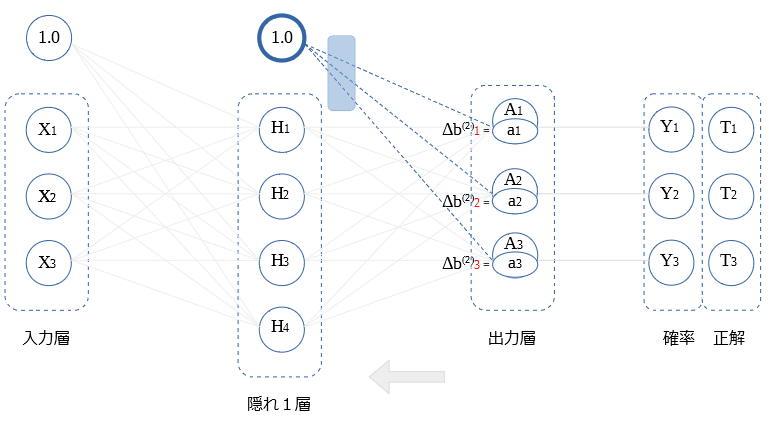
逆伝播値が、そのまま バイアスの重み微分値になります。
式を示します。
$$Δ b_i ^{(2)} = a_i$$
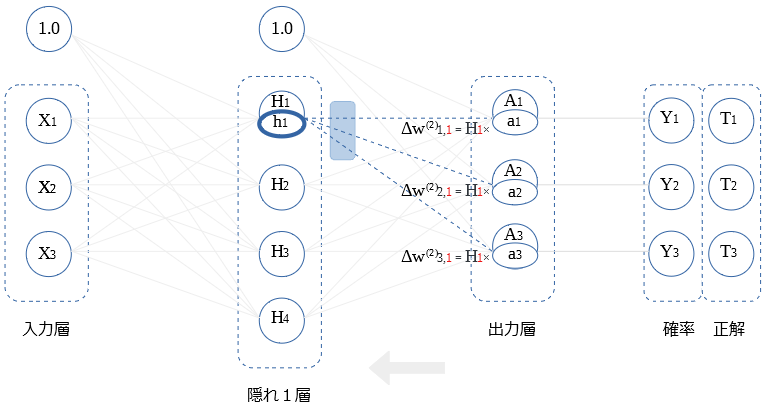
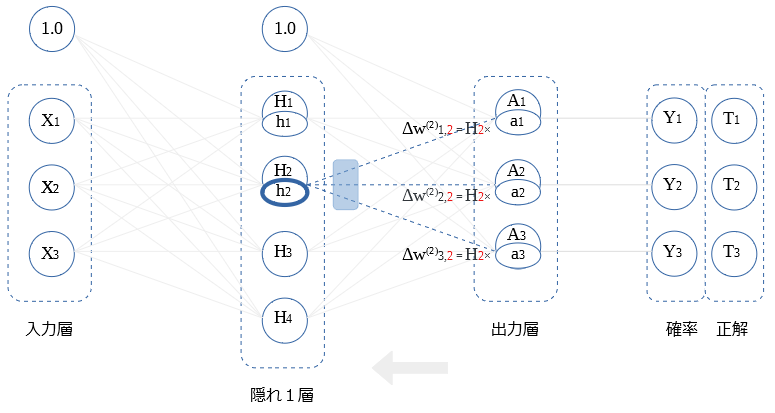
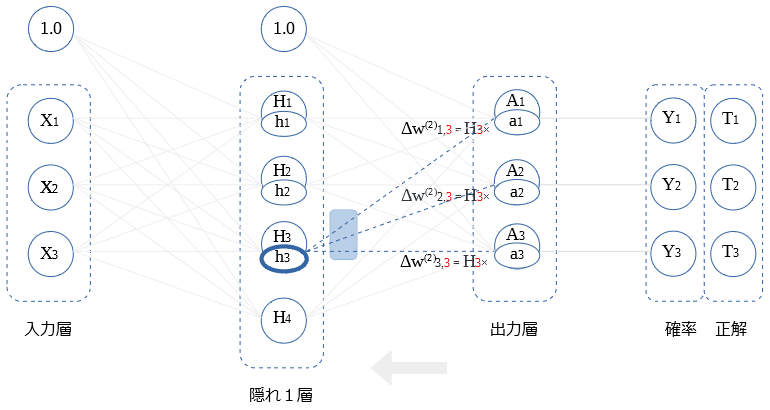
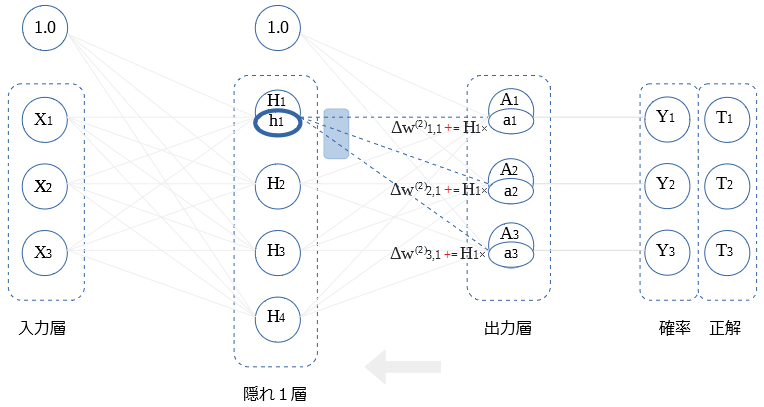
前層〇との重み微分の式を示します。
$$Δ w_{i,1} ^{(2)} = H_1 a_i$$
$H_2$ ~ $H_4$との 重み微分の算出も同様です。図示します。
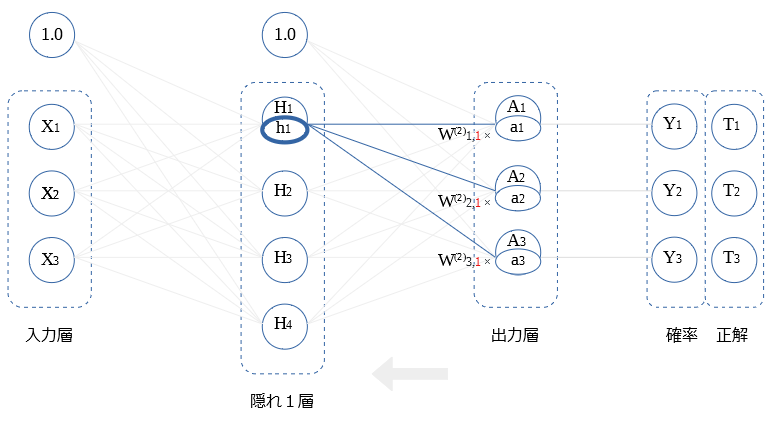
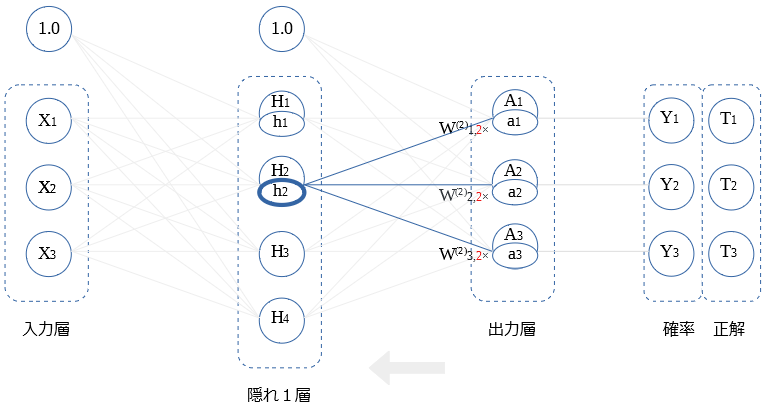
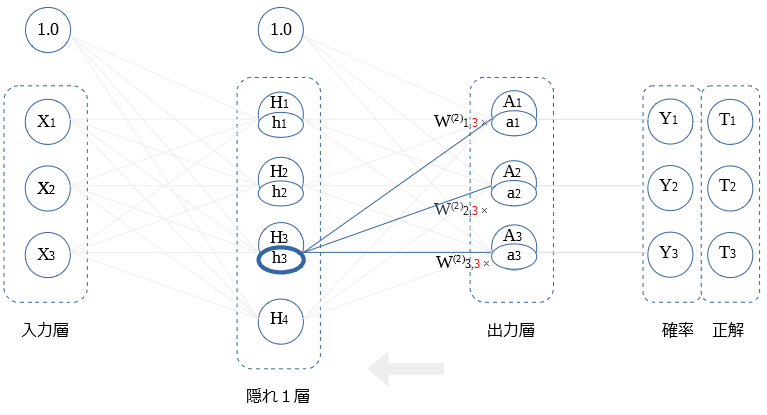
隠れ1層 ← 出力層 (逆伝播値)
前層〇の 逆伝播値 の式を示します。
$$h_1= W_{1,1}^{(2)}a_1 + W_{2,1}^{(2)}a_2+ W_{3,1}^{(2)}a_3$$
$$ = \sum_i W_{i,1}^{(2)}a_i$$
$H_2$ ~ $H_4$との 重み微分の算出も同様です。図示します。
逆伝播 ReLU
順伝播時に0 となった〇は、逆伝播値を0 にする。
逆伝播 ReLU(h) = \left\{
\begin{array}{ll}
h & (0 \lt H) \\
0 & (H \leqq 0)
\end{array}
\right.
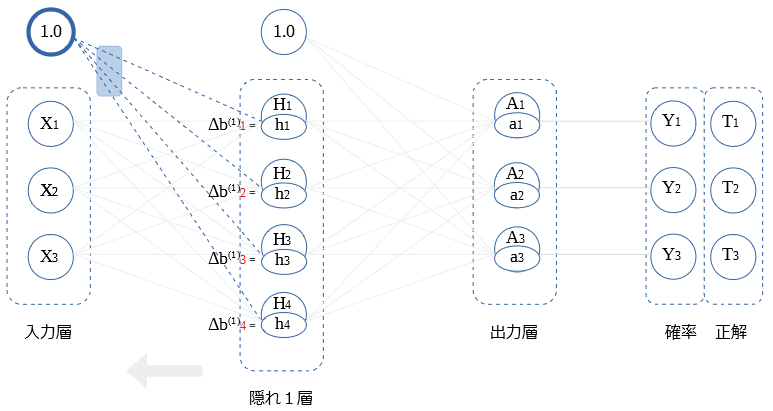
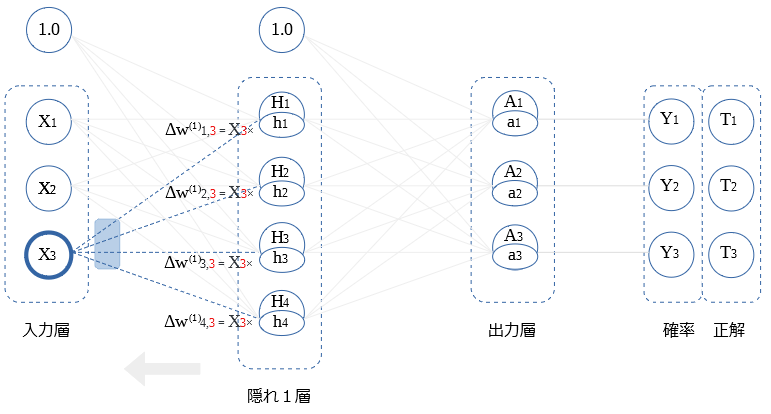
入力層 ← 隠れ1層 (重み微分値)
逆伝播値が、そのまま バイアスの重み微分値になります。
バイアスとの重み微分の式を示します。
$$Δ b_i ^{(1)} = h_i$$
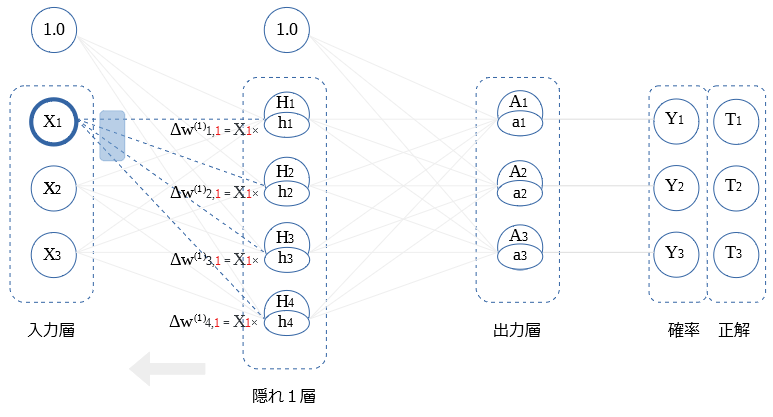
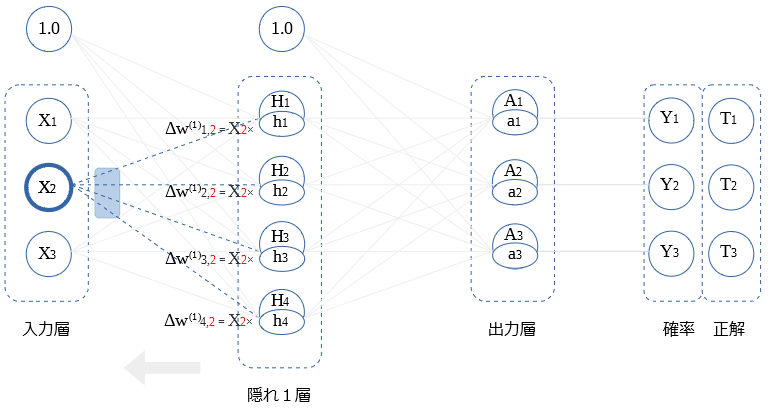
前層〇との重み微分の式を示します。
$$Δ w_{i,1} ^{(1)} = X_1 h_i$$
$X_2$, $X_3$との 重み微分の算出も同様です。図示します。
ミニバッチ処理での 重み微分値
ミニバッチ処理では、複数枚の画像を用いて、重み微分値を求めます。
ミニバッチの開始時に 重み微分値をクリア、以後ミニバッチ期間内で累積した値で、重みを補正します。
ミニバッチ時の、重み微分値の累積を、バイアスと 〇 それぞれ1つ図示します。
重み更新
画像毎の順伝播と逆伝播を、ミニバッチの枚数分行い、加算していった $ΔB$ , $ΔW$ を用いて、$B$ , $W$ の値を更新します。
確率的勾配降下法(Stochastic Gradient Descent) 略称"SGD" での更新式を示します。
$$B=B-η ΔB$$
$$W=W-η ΔW$$
$η$ は学習係数を示し、0.01や0.001といった値を用います。
重み初期値
活性化関数にReLUを用いる場合、nを前層の〇数とすると、各$W$の初期値は$\sqrt{\frac{2}{n}} $ を標準偏差とするガウス分布が適すようです。
Mind言語でのガウス分布の生成は「Mind言語で 疑似乱数関数 を作ってみた」を参考下さい。
次記事
[Mind で Neural Network (SGD)] (http://qiita.com/t-tkd3a/items/6fc76b6874a2d240063e)