概要
Mind で Neural Network (SGD) からの続きです。
重み勾配の 更新方法を SDG から adam に変えた版を公開します。
背景
Deep Learning についての勉強をはじめました。
基本の ニューラルネットワークを 実装できる程度に理解することを 第一の目標としてます。
参考図書として
を用いてます。
読み進めながら 処理の内容を 疑似コードで メモ書きしていたところ、
『日本語プログラミング言語「Mind」最新版をリリースしました』の記事に出会い、言語仕様を調べたところ、メモ書きの 疑似コードが そのまま動きそうな予感で テンション上がり Mind で実装していくことにしました。
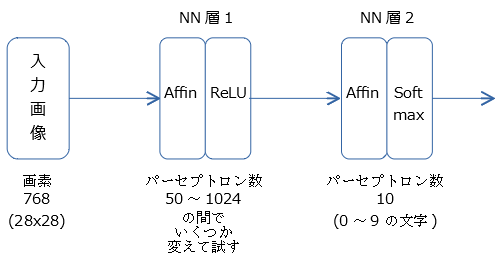
実装したニューラルネットワークの構成
隠れ層1つの、シンプルなニューラルネットワークです。
隠れ層のパーセプトロン数により 性能が変わると予想し 50個と1024個で実行しました。
adam
Mind で Neural Network (準備編2) 順伝播・逆伝播 図解の「重み更新」の項で、$ΔB$と$ΔW$ から $B$と$W$ を更新する式 に、前回はSGD アルゴリズムを用いましたが、今回は adam アルゴリズムを用います。
参考論文:Adam: A Method for Stochastic Optimization
学習係数
α=0.001\\β_1=0.9\\β_2=0.999
更新式
$ΔWからWを更新での例$
lr= α{\frac{\sqrt{1-β_2^t}}{(1-β_1^t)}}
m_{t} = ΔW(1-β_1)+β_1m_{t-1}
v_{t} = ΔW^2(1-β_2)+β_2v_{t-1}
W=W-lr{\frac{m_t}{\sqrt{v_t+0.0000001}}}
$ΔBからBの更新も同様$
ソースコード
4ソースコード構成です。
「Mind言語で 疑似乱数関数 を作ってみた」と、
「Mind で Neural Network (準備編3) 文字画像の読み込みの改良」と、
下記に公開する2本です。
NN2L.src
NN層1パーセプトロン数は 数値 1024。
NN層2パーセプトロン数は 数値 分類数。
※ SDGのソースからは、ループ内の回数値周りを'回数'と'外側回数'を用いるように変更。
NN層1は 構造体
W1は 小数変数
B1は 小数変数
順値1は 小数変数
逆伝播値1は 小数変数
dW1は 小数変数
dB1は 小数変数
W配列1は
画素数の W1
dW配列1は
画素数の dW1
パーセプトロン1は
順値1と
逆伝播値1と
W配列1と B1と
dW配列1と dB1と
全体は
NN層1パーセプトロン数の パーセプトロン1
。
※ -- NN層2は出力層 --
NN層2は 構造体
W2は 小数変数
B2は 小数変数
順値2は 小数変数
逆伝播値2は 小数変数
dW2は 小数変数
dB2は 小数変数
W配列2は
NN層1パーセプトロン数の W2
dW配列2は
NN層1パーセプトロン数の dW2
パーセプトロン2は
順値2と
逆伝播値2と
W配列2と B2と
dW配列2と dB2と
全体は
NN層2パーセプトロン数の パーセプトロン2
。
ソフトマックス層は 構造体
S総和は 小数変数
S各予測値は 小数変数
S各誤差値は 小数変数
直近正否は 小数変数 ※1.0:正解 0.0:間違い※
直近誤差エントロピーは 小数変数
予測値配列Sは
分類数の S各予測値
誤差値配列Sは
分類数の S各誤差値
全体は
直近正否と
直近誤差エントロピーと
予測値配列Sと
誤差値配列Sと
S総和
。
バッチカウンタは 変数。
検証回数は 変数。
ニューラルネット初期化とは
PTは 外側回数と 等価
Iは 回数と 等価
Rは 小数変数
シグマ1は 小数変数
シグマ2は 小数変数
NN層1を クリア
NN層2を クリア
ソフトマックス層を クリア
0を バッチカウンタに 入れる
0を 検証回数に 入れる
画素数を 小数化し シグマ1に 入れる
[シグマ1 := sqrt( 2.0 / シグマ1 ) ]
NN層1パーセプトロン数を 小数化し シグマ2に 入れる
[シグマ2 := sqrt( 2.0 / シグマ2 ) ]
※ -- NN層1 の 重み1 と バイアス1 --
NN層1パーセプトロン数を 回数指定して ※PT
画素数を 回数指定して、※I
※ 「Lv1 W(」を 表示し、 PTを 数値表示し、 「 , 」を 表示し、 Iを 数値表示し、 「)」を 表示し、 改行
ガウス分布乱数( 0.0 , シグマ1 )を W1(PT,I)に 入れる
繰り返す ※PT
繰り返す ※I
NN層1パーセプトロン数を 回数指定して
※ 「Lv1 B(」を 表示し、 回数を 数値表示し、 「) 」を 表示し、
ガウス分布乱数( 0.0 , シグマ1 )を B1(回数)に 入れる
※ B1(回数)を 簡易小数表示し 改行
繰り返す
※ -- NN層2 の 重み2 と バイアス2 --
NN層2パーセプトロン数を 回数指定して、※PT
NN層1パーセプトロン数を 回数指定して、※I
※ 「Lv2 W(」を 表示し、 PTを 数値表示し、 「 , 」を 表示し、 Iを 数値表示し、 「)」を 表示し、 改行
ガウス分布乱数( 0.0 , シグマ2 )を W2(PT,I)に 入れる
繰り返す ※PT
繰り返す ※I
NN層2パーセプトロン数を 回数指定して、
※ 「Lv2 B(」を 表示し、 回数を 数値表示し、 「) 」を 表示し、
ガウス分布乱数( 0.0 , シグマ2 )を B2(回数)に 入れる
※ B2(回数)を 簡易小数表示し 改行
繰り返す
「ニューラルネット初期化 完了」を 表示し 改行
。
NN順伝播とは 関数 整数入力(画像番号)
画像番号は 変数
Zは 小数変数
NN層2最大値は 小数変数
NN層2最大インデックスは 変数
エントロピーは 小数変数
En1は 小数変数
正値は 変数
PTは 外側回数と 等価
Iは 回数と 等価
※ -- 変数初期化 --
画像番号に 入れる
NN層2最大値を クリア
S総和を クリア
f0.0を エントロピーに 入れる
NN層2最大インデックスを クリア
※ 「画像 → NN層1」を 表示し 改行
※ 画像 → NN層1
NN層1パーセプトロン数を 回数指定し、※PT
[Z := B1(回数)]
画素数を 回数指定し、※I, 外側:PT
[Z := 輝度値(画像番号,I) × W1(PT,I) + Z ]
繰り返す
※ ReLU
Zが f0.0より f小さい ならば
f0.0を 順値1(回数)に 入れる
さもなければ
Zを 順値1(回数)に 入れる
つぎに
繰り返す
※ 「NN層1 → NN層2」を 表示し 改行
※ NN層1 → NN層2
順値2(1)を NN層2最大値に 入れる
1を NN層2最大インデックスに 入れる
NN層2パーセプトロン数を 回数指定し、※PT
[Z := B2(回数)]
NN層1パーセプトロン数を 回数指定し、※I, 外側:PT
[Z := 順値1(I) × W2(PT,I) + Z]
繰り返す
Zを 順値2(回数)に 入れる
※ 出力層へのAffinは ReLUしない。※
※ NN層2最大値
順値2(回数)が NN層2最大値より f大きい ならば
順値2(回数)を NN層2最大値に 入れる
回数を NN層2最大インデックスに 入れる
つぎに
繰り返す
※ 「NN層2 → ソフトマックス層」を 表示し 改行
※ NN層2 → ソフトマックス層
NN層2最大インデックスが 0と 等しい ならば
※ どことも判定されなかった ※
改行
「NN層2最大インデックス 0 」を 表示し
「画像番号:」を 表示し 画像番号を 数値表示し、 改行
NN層2パーセプトロン数を 回数指定し、
[回数 - 1 ]を 数値表示し
「:」を 表示し
順値2(回数)を 簡易小数表示し、
「 」を 表示し
繰り返す
改行
0.0を 直近正否に 入れる
[log( 0.0000001 )]を 直近誤差エントロピーに 入れる
分類数を 回数指定し、
正否( 画像番号, 回数)に -1.0を f掛け S各誤差値(回数)に 入れる
繰り返す
さもなければ
正否(画像番号, NN層2最大インデックス)を 直近正否に 入れる
分類数を 回数指定し、
[exp( 順値2(回数) - NN層2最大値 ) ]を S各予測値(回数)に 入れる
[S総和 := S総和 + S各予測値(回数) ]
繰り返す
分類数を 回数指定し、
[S各予測値(回数) / S総和 ]を S各予測値(回数)に 入れる
[S各予測値(回数) - 正否( 画像番号, 回数) ]を S各誤差値(回数)に 入れる
※ 逆伝播の入力値となる値
繰り返す
正解値(画像番号)に 1を 加え 正値に 入れる
[ log( S各予測値( 正値 ) + 0.0000001 ) ]に -1.0を f掛けし 直近誤差エントロピーに 入れる
つぎに
。
NN逆伝播とは 関数 整数入力(画像番号)
画像番号は 変数
Zは 小数変数
Iは 回数と 等価
PTは 外側回数と 等価
画像番号に 入れる
※ NN層2 (←ソフトマックス層)
分類数を 回数指定し、※PT
S各誤差値(回数)を 逆伝播値2(回数)に 入れる
[dB2(回数) + 逆伝播値2(回数)]を dB2(回数)に 入れる
NN層1パーセプトロン数を 回数指定し、※I , 外側:PT
[dW2(PT,I) + 順値1(I) × 逆伝播値2(PT)]を dW2(PT,I)に 入れる
繰り返す
繰り返す
※ NN層1 (←NN層2)
NN層1パーセプトロン数を 回数指定し、※ PT
※ ReLU 分岐
順値1(回数)が f0.0より 以下 ならば
f0.0を 逆伝播値1(回数)に 入れる
さもなければ
f0.0を Zに 入れる
NN層2パーセプトロン数を 回数指定し、※I, 外側:PT
[Z := 逆伝播値2(I) × W2(I,PT) + Z ]
繰り返す
Zを 逆伝播値1(回数)に 入れる
[dB1(回数) + 逆伝播値1(回数)]を dB1(回数)に 入れる
画素数を 回数指定し、※I , 外側:PT
[dw1(PT,I) + 輝度値(画像番号,I) × 逆伝播値1(PT) ]を dw1(PT,I)に 入れる
繰り返す
つぎに
繰り返す
。
傾き値クリアとは
PTは 外側回数と 等価
Iは 回数と 等価
※ -- NN層1 の dw1 と db1 --
パーセプトロン1の 要素数を 回数指定して、※PT
f0.0を dB1(回数)に 入れる
画素数を 回数指定して、 ※I
f0.0を dW1(PT,I)に 入れる
繰り返す
繰り返す
※ -- NN層2 の 重み2 と バイアス2 --
パーセプトロン2の 要素数を 回数指定して、 ※PT
f0.0を dB2(回数)に 入れる
NN層1パーセプトロン数を 回数指定して、 ※I
f0.0を dW2(PT,I)に 入れる
繰り返す
繰り返す
。
検証とは
エントロピ総和は 小数変数
正否総和は 小数変数
Nは 小数変数
Iは 変数
開始番号は 変数
ループ上限は 変数
エントロピ総和を クリア
正否総和を クリア
[検証回数 := 検証回数 + 1]
[開始番号 := 入力画像数 + 1]
検証画像数を 小数化し Nに 入れる
[ループ上限 := 検証画像数 - 1]
ループ上限を 回数指定して
[I := 開始番号 + 回数 ]
NN順伝播( I )する
[エントロピ総和 := エントロピ総和 + 直近誤差エントロピー]
[正否総和 := 正否総和 + 直近正否]
繰り返す
改行
「検証 」を 表示し、 検証回数を 数値表示し、
「回目 誤差エントロピ:」を 表示し、 エントロピ総和を Nで f割りを 簡易小数表示し、
「 正解率:」を 表示し、 正否総和を Nで f割りを 簡易小数表示し、
改行
。
NN_adam.src
"Random.src"を コンパイル。
"MNISTfiles.src"を コンパイル。
"NN2L.src"を コンパイル。
バッチ画像数は 数値 100。
※ 更新アルゴリズム adam のハイパーパラメータ
adamαは 小数定数 0.001。
adamβ1は 小数定数 0.9。
adamβ2は 小数定数 0.999。
adamNN層1は 構造体
WadamM1は 小数変数
WadamV1は 小数変数
BadamM1は 小数変数
BadamV1は 小数変数
WadamM1配列は
画素数の WadamM1
WadamV1配列は
画素数の WadamV1
adamパーセプトロン1は
WadamM1配列と BadamM1と
WadamV1配列と BadamV1
全体は
NN層1パーセプトロン数の adamパーセプトロン1
。
adamNN層2は 構造体
WadamM2は 小数変数
WadamV2は 小数変数
BadamM2は 小数変数
BadamV2は 小数変数
WadamM2配列は
NN層1パーセプトロン数の WadamM2
WadamV2配列は
NN層1パーセプトロン数の WadamV2
adamパーセプトロン2は
WadamM2配列と BadamM2と
WadamV2配列と BadamV2
全体は
NN層2パーセプトロン数の adamパーセプトロン2
。
adam版重み更新とは
PTは 外側回数と 等価
Iは 回数と 等価
LRは 小数変数
Mは 小数変数
Vは 小数変数
Qは 小数変数
Q2は 小数変数
Tは 小数変数
B1tは 小数変数
B2tは 小数変数
_aaは 小数変数
_ab1は 小数変数
_ab2は 小数変数
_tp1は 小数変数
※ 「adam重み更新() 開始」を 表示し 改行
※共通値
[バッチカウンタ := バッチカウンタ + 1]
バッチカウンタを 小数化し Tに 入れる
adamαを _aaに 入れる
adamβ1を _ab1に 入れる
adamβ2を _ab2に 入れる
※ [B1t := f1.0 - pow( _ab1 , T ) ]
f1.0から pow(_ab1,T)を f引き B1tに 入れる
※ [B2t := f1.0 - pow( _ab2 , T ) ]
f1.0から pow(_ab2,T)を f引き B2tに 入れる
[LR := _aa × sqrt( B2t ) / B1t ]
※ 「------------」を 表示し 改行
※ 「 B1t:」を 表示し、 B1tを 簡易小数表示
※ 「 B2t:」を 表示し、 B2tを 簡易小数表示
※ 「 LR:」を 表示し、 LRを 簡易小数表示
※ 改行
※ -- NN層1 の dw1 と db1 --
パーセプトロン1の 要素数を 回数指定して、 ※PT
※ -- バイアス --
dB1(回数)を Qに 入れる
[Q2 := Q × Q]
※[M := Q - _ab1 × Q + _ab1 × BadamM1(回数) ]
[Q + _ab1 × BadamM1(回数)]から [_ab1 × Q]を f引き Mに 入れる
※[V := Q2 - _ab2 × Q2 + _ab2 × BadamV1(回数) ]
[Q2 + _ab2 × BadamV1(回数)]から [_ab2 × Q2]を f引き Vに 入れる
Mを BadamM1(回数)に 入れる
Vを BadamV1(回数)に 入れる
※ [B1(回数) - LR × M / sqrt( V + 0.00000001 ) ]を B1(回数)に 入れる
[LR × M / sqrt( V + 0.00000001) ]を _tp1に 入れる
B1(回数)から _tp1を f引き B1(回数)に 入れる
※ 「----」を 表示し 改行
※ 「 Q:」を 表示し、 Qを 簡易小数表示
※ 「 Q2:」を 表示し、 Q2を 簡易小数表示
※ 「 M:」を 表示し、 Mを 簡易小数表示
※ 「 V:」を 表示し、 Vを 簡易小数表示
※ 「 _tp1:」を 表示し、 _tp1を 簡易小数表示
※ 「 B1(回数):」を 表示し、 B1(回数)を 簡易小数表示
※ 改行
※ -- 重み --
画素数を 回数指定して、※I , 外側:PT
dW1(PT,I)を Qに 入れる
[Q2 := Q × Q]
※[M := Q - _ab1 × Q + _ab1 × WadamM1(PT,I) ]
[Q + _ab1 × WadamM1(PT,I)]から [_ab1 × Q]を f引き Mに 入れる
※[V := Q2 - _ab2 × Q2 + _ab2 × WadamV1(PT,I) ]
[Q2 + _ab2 × WadamV1(PT,I)]から [_ab2 × Q2]を f引き Vに 入れる
Mを WadamM1(PT,I)に 入れる
Vを WadamV1(PT,I)に 入れる
※[W1(PT,I) - LR × M / sqrt( V + 0.00000001 ) ]を W1(PT,I)に 入れる
W1(PT,I)から [LR × M / sqrt( V + 0.00000001 ) ]を f引き W1(PT,I)に 入れる
繰り返す
繰り返す
※ 「adam 第2層」を 表示し 改行
※ -- NN層2 の dw2 と db2 --
パーセプトロン2の 要素数を 回数指定して、※PT
※ -- バイアス --
dB2(回数)を Qに 入れる
[Q2 := Q × Q]
※[M := Q - _ab1 × Q + _ab1 × BadamM2(回数) ]
[Q + _ab1 × BadamM2(回数)]から [_ab1 × Q]を f引き Mに 入れる
※[V := Q2 - _ab2 × Q2 + _ab2 × BadamV2(回数) ]
[Q2 + _ab2 × BadamV2(回数)]から [_ab2 × Q2]を f引き Vに 入れる
Mを BadamM2(回数)に 入れる
Vを BadamV2(回数)に 入れる
※[B2(回数) - LR × M / sqrt( V + 0.00000001 ) ]を B2(回数)に 入れる
B2(回数)から [LR × M / sqrt( V + 0.00000001 ) ]を f引き B2(回数)に 入れる
※ -- 重み --
パーセプトロン1の 要素数を 回数指定して、※I, 外側:PT
※ 「(PT:」を 表示し、 PTを 数値表示し、 「 , I:」を 表示し、 Iを 数値表示し、 「 )」を 表示し、 改行
dW2(PT,I)を Qに 入れる
[Q2 := Q × Q]
※[M := Q - _ab1 × Q + _ab1 × WadamM2(PT,I) ]
[Q + _ab1 × WadamM2(PT,I)]から [_ab1 × Q]を f引き Mに 入れる
※[V := Q2 - _ab2 × Q2 + _ab2 × WadamV2(PT,I) ]
[Q2 + _ab2 × WadamV2(PT,I)]から [_ab2 × Q2]を f引き Vに 入れる
Mを WadamM2(PT,I)に 入れる
Vを WadamV2(PT,I)に 入れる
※[W2(PT,I) - LR × M / sqrt( V + 0.00000001 ) ]を W2(PT,I)に 入れる
W2(PT,I)から [LR × M / sqrt( V + 0.00000001 ) ]を f引き W2(PT,I)に 入れる
繰り返す
繰り返す
※ 「adam重み更新() 完」を 表示し 改行
傾き値クリアをする
。
adam版エポック1巡とは
バッチ分割数は 変数
開始画像番号は 変数
Cntは 変数
Iは 変数
[バッチ分割数 := 入力画像数 / バッチ画像数]
バッチ分割数を 回数指定して、 回数から 1を 引くを Cntに 入れる
[開始画像番号 := バッチ画像数 × Cnt ]
※ 「(開始:」を 表示し、 開始画像番号を 数値表示し、 「, バッチ画像数:」を 表示し、 バッチ画像数を 数値表示し、 「)」を 表示し 改行
バッチ画像数を 回数指定して、
[I := 開始画像番号 + 回数 ]
NN順伝播( I )する
NN逆伝播( I )する
繰り返す
adam版重み更新をする
「+」を 表示する
繰り返す
改行
検証する
。
テスト00とは
「傾き値クリア()」を 表示し 改行
傾き値クリア
「傾き値クリア()完」を 表示し 改行
「NN順伝播()」を 表示し 改行
NN順伝播(10002)する ※実行OK
「NN順伝播()完」を 表示し 改行
「NN逆伝播()」を 表示し 改行
NN逆伝播(10002)
「NN逆伝播()完」を 表示し 改行
「重み更新()」を 表示し 改行
adam版重み更新する
「重み更新()完」を 表示し 改行
「検証()」を 表示し 改行
検証する
「検証()完」を 表示し 改行
。
メインとは
開始時刻値は 変数
終了時刻値は 変数
「メイン開始」を 表示し 改行
20170316を 乱数種値に 入れる
MNISTファイル読込をする
ニューラルネット初期化をする
adamNN層1を クリア
adamNN層2を クリア
「NN層1パーセプトロン数 :」を 表示し、 NN層1パーセプトロン数を 数値表示し、
「 ,adam 」を 表示し、
「 ,入力画像数:」を 表示し、 入力画像数を 数値表示し、
「 ,検証画像数:」を 表示し、 検証画像数を 数値表示し、
改行
日時を値で得て 開始時刻値に 入れる
※ テスト00
30を 回数指定し、 adam版エポック1巡を 繰り返す
日時を値で得て 終了時刻値に 入れる
[ 終了時刻値 - 開始時刻値 ]を 数値表示し、 「(秒)」を 表示し、 改行
スタック検査し
。
動作結果
パーセプトロン数50
NN層1パーセプトロン数 :50 ,adam ,入力画像数:10000 ,検証画像数:1000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 1回目 誤差エントロピ:0.52776 正解率:0.81800
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 2回目 誤差エントロピ:0.39263 正解率:0.85000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 3回目 誤差エントロピ:0.34209 正解率:0.86300
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 4回目 誤差エントロピ:0.31280 正解率:0.86700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 5回目 誤差エントロピ:0.29276 正解率:0.87500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 6回目 誤差エントロピ:0.27817 正解率:0.87900
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 7回目 誤差エントロピ:0.26548 正解率:0.87800
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 8回目 誤差エントロピ:0.25505 正解率:0.88500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 9回目 誤差エントロピ:0.24538 正解率:0.88900
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 10回目 誤差エントロピ:0.23731 正解率:0.89000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 11回目 誤差エントロピ:0.23024 正解率:0.89400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 12回目 誤差エントロピ:0.22414 正解率:0.89500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 13回目 誤差エントロピ:0.21868 正解率:0.89800
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 14回目 誤差エントロピ:0.21320 正解率:0.89900
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 15回目 誤差エントロピ:0.20942 正解率:0.90100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 16回目 誤差エントロピ:0.20549 正解率:0.90200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 17回目 誤差エントロピ:0.20259 正解率:0.89900
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 18回目 誤差エントロピ:0.19996 正解率:0.90000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 19回目 誤差エントロピ:0.19757 正解率:0.90100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 20回目 誤差エントロピ:0.19498 正解率:0.90100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 21回目 誤差エントロピ:0.19323 正解率:0.90200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 22回目 誤差エントロピ:0.19182 正解率:0.90200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 23回目 誤差エントロピ:0.19022 正解率:0.90300
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 24回目 誤差エントロピ:0.18881 正解率:0.90400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 25回目 誤差エントロピ:0.18724 正解率:0.90500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 26回目 誤差エントロピ:0.18640 正解率:0.90700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 27回目 誤差エントロピ:0.18486 正解率:0.90700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 28回目 誤差エントロピ:0.18397 正解率:0.90800
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 29回目 誤差エントロピ:0.18366 正解率:0.90800
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 30回目 誤差エントロピ:0.18320 正解率:0.90800
パーセプトロン数1024
C:Mind\t02_NN>NN_adam
メイン開始
C:\data\MNIST\train-images-idx3-ubyte 読込開始
読込完了
C:\data\MNIST\t10k-images-idx3-ubyte 読込開始
読込完了
C:\data\MNIST\train-labels-idx1-ubyte 読込開始
読込完了
C:\data\MNIST\t10k-labels-idx1-ubyte 読込開始
読込完了
1(秒)
ニューラルネット初期化 完了
NN層1パーセプトロン数 :1024 ,adam ,入力画像数:10000 ,検証画像数:1000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 1回目 誤差エントロピ:0.33544 正解率:0.83300
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 2回目 誤差エントロピ:0.26192 正解率:0.86300
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 3回目 誤差エントロピ:0.20539 正解率:0.89200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 4回目 誤差エントロピ:0.17682 正解率:0.89700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 5回目 誤差エントロピ:0.16251 正解率:0.90800
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 6回目 誤差エントロピ:0.15965 正解率:0.90900
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 7回目 誤差エントロピ:0.15760 正解率:0.91000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 8回目 誤差エントロピ:0.14875 正解率:0.91500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 9回目 誤差エントロピ:0.14233 正解率:0.91500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 10回目 誤差エントロピ:0.13144 正解率:0.92000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 11回目 誤差エントロピ:0.12799 正解率:0.92100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 12回目 誤差エントロピ:0.12474 正解率:0.92000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 13回目 誤差エントロピ:0.12526 正解率:0.92300
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 14回目 誤差エントロピ:0.12641 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 15回目 誤差エントロピ:0.12734 正解率:0.92300
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 16回目 誤差エントロピ:0.12800 正解率:0.92200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 17回目 誤差エントロピ:0.12856 正解率:0.92200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 18回目 誤差エントロピ:0.12873 正解率:0.92200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 19回目 誤差エントロピ:0.12951 正解率:0.92200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 20回目 誤差エントロピ:0.13009 正解率:0.92100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 21回目 誤差エントロピ:0.13050 正解率:0.92100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 22回目 誤差エントロピ:0.13115 正解率:0.92100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 23回目 誤差エントロピ:0.13162 正解率:0.92200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 24回目 誤差エントロピ:0.13202 正解率:0.92200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 25回目 誤差エントロピ:0.13265 正解率:0.92200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 26回目 誤差エントロピ:0.13319 正解率:0.92200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 27回目 誤差エントロピ:0.13380 正解率:0.92200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 28回目 誤差エントロピ:0.13430 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 29回目 誤差エントロピ:0.13493 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 30回目 誤差エントロピ:0.13533 正解率:0.92400
173016(秒)
回数を進めると、誤差エントロピが下がっている。
パーセプトロン数が1024の場合には、正解率は92%程度ある。
ニューラルネットワークの学習がうまく機能していると判断します。
SGD と adam にて、途中経過では差があるものの、30回目での正解率に差は出ませんでした。
どちらも学習係数に定番の値を用いてるためなのでしょうか?
シンプルなネットワークだからでしょうか...。
計算時間
前回のSGDに比べ 体感 1.5倍ほどの時間を要しています。
1024パーセプトロンの計算を行う際に、所要時間算出させる処理を追加しました。
1024パーセプトロンの場合には 173016(秒)要してます。
次記事予定
畳み込みニューラルネットワーク(Convolutional Neural Network)の理解のため、図解と 実装を行って行きたいかと考えてます。