概要
Mind で Neural Network (準備編2) 順伝播・逆伝播 図解 からの続きです。
前回で図解した式を基に実装を行った ニューラルネットワークのソースコードと 実行結果を公開します。
高速化等のアドバイスが頂けると助かります。
背景
Deep Learning についての勉強をはじめました。
基本の ニューラルネットワークを 実装できる程度に理解することを 第一の目標としてます。
参考図書として
を用いてます。
読み進めながら 処理の内容を 疑似コードで メモ書きしていたところ、
『日本語プログラミング言語「Mind」最新版をリリースしました』の記事に出会い、言語仕様を調べたところ、メモ書きの 疑似コードが そのまま動きそうな予感で テンション上がり Mind で実装していくことにしました。
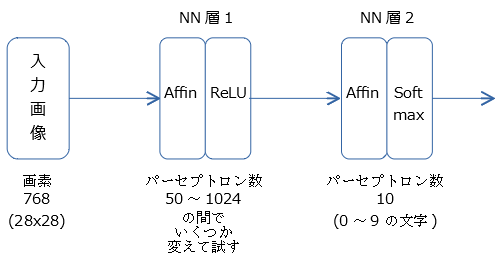
実装したニューラルネットワークの構成
隠れ層1つの、シンプルなニューラルネットワークです。
隠れ層のパーセプトロン数により 性能が変わると予想し 50個と1024個で実行しました。
ソースコード
4ソースコード ファイル構成です。
すでに2つのソースコード ファイルは、
「Mind言語で 疑似乱数関数 を作ってみた」と、
「Mind で Neural Network (準備編1) 文字画像の読み込み」にて
公開してあります。
残り2つを公開します。
NN2L.src
※このソースでは、隠れ層1つの ニューラルネットワークの構造体宣言と
※ 順伝播、逆伝播、検証の処理を実装する。
※
NN層1パーセプトロン数は 数値 1024。
NN層2パーセプトロン数は 数値 分類数。
NN層1は 構造体
W1は 小数変数
B1は 小数変数
順値1は 小数変数
逆伝播値1は 小数変数
dW1は 小数変数
dB1は 小数変数
W配列1は
画素数の W1
dW配列1は
画素数の dW1
パーセプトロン1は
順値1と
逆伝播値1と
W配列1と B1と
dW配列1と dB1と
全体は
NN層1パーセプトロン数の パーセプトロン1
。
※ -- NN層2は出力層 --
NN層2は 構造体
W2は 小数変数
B2は 小数変数
順値2は 小数変数
逆伝播値2は 小数変数
dW2は 小数変数
dB2は 小数変数
W配列2は
NN層1パーセプトロン数の W2
dW配列2は
NN層1パーセプトロン数の dW2
パーセプトロン2は
順値2と
逆伝播値2と
W配列2と B2と
dW配列2と dB2と
全体は
NN層2パーセプトロン数の パーセプトロン2
。
ソフトマックス層は 構造体
S総和は 小数変数
S各予測値は 小数変数
S各誤差値は 小数変数
直近正否は 小数変数 ※1.0:正解 0.0:間違い※
直近誤差エントロピーは 小数変数
予測値配列Sは
分類数の S各予測値
誤差値配列Sは
分類数の S各誤差値
全体は
直近正否と
直近誤差エントロピーと
予測値配列Sと
誤差値配列Sと
S総和
。
バッチカウンタは 変数。
検証回数は 変数。
ニューラルネット初期化とは
PTは 変数
Jは 変数
Rは 小数変数
シグマ1は 小数変数
シグマ2は 小数変数
NN層1を クリア
NN層2を クリア
ソフトマックス層を クリア
0を バッチカウンタに 入れる
0を 検証回数に 入れる
画素数を 小数化し シグマ1に 入れる
[シグマ1 := sqrt( 2.0 / シグマ1 ) ]
NN層1パーセプトロン数を 小数化し シグマ2に 入れる
[シグマ2 := sqrt( 2.0 / シグマ2 ) ]
※ -- NN層1 の 重み1 と バイアス1 --
パーセプトロン1の 要素数を 回数指定して、 回数を PTに 入れる
画素数を 回数指定して、 回数を Jに 入れる
※「Lv1 W(」を 表示し、 PTを 数値表示し、 「 , 」を 表示し、 Jを 数値表示し、 「)」を 表示し、 改行
ガウス分布乱数( 0.0 , シグマ1 )を W1(PT,J)に 入れる
繰り返す ※PT
※ 「Lv1 B(」を 表示し、 PTを 数値表示し、 「) 」を 表示し、
ガウス分布乱数( 0.0 , シグマ1 )を B1(PT)に 入れる
※ B1(PT)を 簡易小数表示し 改行
繰り返す ※J
※ -- NN層2 の 重み2 と バイアス2 --
パーセプトロン2の 要素数を 回数指定して、 回数を PTに 入れる
NN層1パーセプトロン数を 回数指定して、 回数を Jに 入れる
※「Lv2 W(」を 表示し、 PTを 数値表示し、 「 , 」を 表示し、 Jを 数値表示し、 「)」を 表示し、 改行
ガウス分布乱数( 0.0 , シグマ2 )を W2(PT,J)に 入れる
繰り返す ※PT
※ 「Lv2 B(」を 表示し、 PTを 数値表示し、 「) 」を 表示し、
ガウス分布乱数( 0.0 , シグマ2 )を B2(PT)に 入れる
※ B2(PT)を 簡易小数表示し 改行
繰り返す ※J
「ニューラルネット初期化 完了」を 表示し 改行
。
NN順伝播とは 関数 整数入力(画像番号)
画像番号は 変数
Iは 変数
PTは 変数
Zは 小数変数
NN層2最大値は 小数変数
NN層2最大インデックスは 変数
エントロピーは 小数変数
En1は 小数変数
※ -- 変数初期化 --
画像番号に 入れる
NN層2最大値を クリア
S総和を クリア
f0.0を エントロピーに 入れる
NN層2最大インデックスを クリア
※ 画像 → NN層1
NN層1パーセプトロン数を 回数指定し、 回数を PTに 入れる
[Z := B1(PT)]
画素数を 回数指定し、 回数を Iに 入れる
[Z := 輝度値(画像番号,I) × W1(PT,I) + Z ]
繰り返す
※ ReLU
Zが f0.0より f小さい ならば
f0.0を 順値1(PT)に 入れる
さもなければ
Zを 順値1(PT)に 入れる
つぎに
繰り返す
※ NN層1 → NN層2
順値2(1)を NN層2最大値に 入れる
1を NN層2最大インデックスに 入れる
NN層2パーセプトロン数を 回数指定し、 回数を PTに 入れる
[Z := B2(PT)]
NN層1パーセプトロン数を 回数指定し、 回数を Iに 入れる
[Z := 順値1(I) × W2(PT,I) + Z]
繰り返す
Zを 順値2(PT)に 入れる
※ 出力層へのAffinは ReLUしない。※
※ NN層2最大値
順値2(PT)が NN層2最大値より f大きい ならば
順値2(PT)を NN層2最大値に 入れる
PTを NN層2最大インデックスに 入れる
つぎに
繰り返す
※ NN層2 → ソフトマックス層
NN層2最大インデックスが 0と 等しい ならば
※ どことも判定されなかった ※
改行
「NN層2最大インデックス 0 」を 表示し
「画像番号:」を 表示し 画像番号を 数値表示し、 改行
NN層2パーセプトロン数を 回数指定し、 回数を PTに 入れる
PTから 1を 引き 数値表示し
「:」を 表示し
順値2(PT)を 簡易小数表示し、
「 」を 表示し
繰り返す
改行
0.0を 直近正否に 入れる
[log( 0.0000001 )]を 直近誤差エントロピーに 入れる
分類数を 回数指定し、 回数を Iに 入れる
正否( 画像番号, I)に -1.0を f掛け S各誤差値(I)に 入れる
繰り返す
さもなければ
正否(画像番号, NN層2最大インデックス)を 直近正否に 入れる
分類数を 回数指定し、 回数を Iに 入れる
[exp( 順値2(I) - NN層2最大値 ) ]を S各予測値(I)に 入れる
[S総和 := S総和 + S各予測値(I) ]
繰り返す
分類数を 回数指定し、 回数を Iに 入れる
[S各予測値(I) / S総和 ]を S各予測値(I)に 入れる
[S各予測値(I) - 正否( 画像番号, I) ]を S各誤差値(I)に 入れる
※ 逆伝播の入力値となる値
繰り返す
正解値(画像番号)に 1を 加え Iに 入れる
[ log( S各予測値( I ) + 0.0000001 ) ]に -1.0を f掛けし 直近誤差エントロピーに 入れる
つぎに
。
NN逆伝播とは 関数 整数入力(画像番号)
画像番号は 変数
Iは 変数
PTは 変数
Zは 小数変数
画像番号に 入れる
※ NN層2 (←ソフトマックス層)
分類数を 回数指定し、 回数を PTに 入れる
S各誤差値(PT)を 逆伝播値2(PT)に 入れる
[dB2(PT) + 逆伝播値2(PT)]を dB2(PT)に 入れる
NN層1パーセプトロン数を 回数指定し、 回数を Iに 入れる
[dW2(PT,I) + 順値1(I) × 逆伝播値2(PT)]を dW2(PT,I)に 入れる
繰り返す
繰り返す
※ NN層1 (←NN層2)
NN層1パーセプトロン数を 回数指定し、 回数を PTに 入れる
※ ReLU 分岐
順値1(PT)が f0.0より 以下 ならば
f0.0を 逆伝播値1(PT)に 入れる
さもなければ
f0.0を Zに 入れる
NN層2パーセプトロン数を 回数指定し、 回数を Iに 入れる
[Z := 逆伝播値2(I) × W2(I,PT) + Z ]
繰り返す
Zを 逆伝播値1(PT)に 入れる
[dB1(PT) + 逆伝播値1(PT)]を dB1(PT)に 入れる
画素数を 回数指定し、 回数を Iに 入れる
[dw1(PT,I) + 輝度値(画像番号,I) × 逆伝播値1(PT) ]を dw1(PT,I)に 入れる
繰り返す
つぎに
繰り返す
。
傾き値クリアとは
PTは 変数
Iは 変数
※ -- NN層1 の dw1 と db1 --
パーセプトロン1の 要素数を 回数指定して、 回数を PTに 入れる
f0.0を dB1(PT)に 入れる
画素数を 回数指定して、 回数を Iに 入れる
f0.0を dW1(PT,I)に 入れる
繰り返す
繰り返す
※ -- NN層2 の 重み2 と バイアス2 --
パーセプトロン2の 要素数を 回数指定して、 回数を PTに 入れる
f0.0を dB2(PT)に 入れる
NN層1パーセプトロン数を 回数指定して、 回数を Iに 入れる
f0.0を dW2(PT,I)に 入れる
繰り返す
繰り返す
。
検証とは
エントロピ総和は 小数変数
正否総和は 小数変数
Nは 小数変数
Iは 変数
開始番号は 変数
ループ上限は 変数
エントロピ総和を クリア
正否総和を クリア
[検証回数 := 検証回数 + 1]
[開始番号 := 入力画像数 + 1]
検証画像数を 小数化し Nに 入れる
[ループ上限 := 検証画像数 - 1]
ループ上限を 回数指定して
[I := 開始番号 + 回数 ]
NN順伝播( I )する
[エントロピ総和 := エントロピ総和 + 直近誤差エントロピー]
[正否総和 := 正否総和 + 直近正否]
繰り返す
改行
「検証 」を 表示し、 検証回数を 数値表示し、
「回目 誤差エントロピ:」を 表示し、 エントロピ総和を Nで f割りを 簡易小数表示し、
「 正解率:」を 表示し、 正否総和を Nで f割りを 簡易小数表示し、
改行
。
NN2L_SGD.src
"Random.src"を コンパイル。
"MNISTfiles.src"を コンパイル。
"NN2L.src"を コンパイル。
バッチ画像数は 数値 100。
※ 更新アルゴリズム SGD のハイパーパラメータ
sgdLRは 小数定数 0.01。
SGD版重み更新とは
PTは 変数
Iは 変数
Cは 小数変数
※ 画素数を 回数指定して、 回数を Iに 入れる
※ パーセプトロン1の 要素数を 回数指定して、 回数を PTに 入れる
※ dW1(PT,I)を 小数2桁表示し 「 」を 表示し
※ 繰り返す
※ 改行
※ 繰り返す
※ -- NN層1 の dw1 と db1 --
パーセプトロン1の 要素数を 回数指定して、 回数を PTに 入れる
※ -- バイアス --
※[C := sgdLR × dB1(PT)]
sgdLRを dB1(PT)に f掛け Cに 入れる
※ 改行
※ 「(」を 表示し、
※ B1(PT)を 小数2桁表示し、 「,」を 表示し
※ dB1(PT)を 小数2桁表示し、 「,」を 表示し
※ Cを 小数2桁表示し、 「,」を 表示し
[B1(PT) - C]を B1(PT)に 入れる
※ B1(PT)を 小数2桁表示し、 「) 」を 表示
※ -- 重み --
画素数を 回数指定して、 回数を Iに 入れる
※[C := sgdLR × dW1(PT,I)]
sgdLRを dW1(PT,I)に f掛け Cに 入れる
※ 「(」を 表示し、
※ W1(PT,I)を 小数2桁表示し、 「,」を 表示し
※ dW1(PT,I)を 小数2桁表示し、 「,」を 表示し
※ Cを 小数2桁表示し、 「,」を 表示し
[W1(PT,I) - C]を W1(PT,I)に 入れる
※ W1(PT,I)を 小数2桁表示し、 「) 」を 表示し
※ 改行
繰り返す
繰り返す
※ -- NN層2 の dw2 と db2 --
パーセプトロン2の 要素数を 回数指定して、 回数を PTに 入れる
※ -- バイアス --
※[C := sgdLR × dB2(PT)]
sgdLRを dB2(PT)に f掛け Cに 入れる
[B2(PT) - C]を B2(PT)に 入れる
※ -- 重み --
パーセプトロン1の 要素数を 回数指定して、 回数を Iに 入れる
※[C := sgdLR × dW2(PT,I)]
sgdLRを dW2(PT,I)に f掛け Cに 入れる
[W2(PT,I) - C]を W2(PT,I)に 入れる
繰り返す
繰り返す
傾き値クリアをする
。
SGD版エポック1巡とは
バッチ分割数は 変数
開始画像番号は 変数
Cntは 変数
Iは 変数
[バッチ分割数 := 入力画像数 / バッチ画像数]
バッチ分割数を 回数指定して、 回数から 1を 引くを Cntに 入れる
[開始画像番号 := バッチ画像数 × Cnt ]
※ SGD版バッチ処理(開始番号 , バッチ画像数)する
※ 「(開始:」を 表示し、 開始画像番号を 数値表示し、 「, バッチ画像数:」を 表示し、 バッチ画像数を 数値表示し、 「)」を 表示し 改行
バッチ画像数を 回数指定して、
[I := 開始画像番号 + 回数 ]
NN順伝播( I )する
NN逆伝播( I )する
繰り返す
SGD版重み更新をする
「+」を 表示する
繰り返す
改行
検証する
。
メインとは
「メイン開始」を 表示し 改行
20170316を 乱数種値に 入れる
MNISTファイル読込をする
ニューラルネット初期化をする
「NN層1パーセプトロン数 :」を 表示し、 NN層1パーセプトロン数を 数値表示し、
「 ,SDG 」を 表示し、
「 ,入力画像数:」を 表示し、 入力画像数を 数値表示し、
「 ,検証画像数:」を 表示し、 検証画像数を 数値表示し、
改行
30を 回数指定し、
SGD版エポック1巡を
繰り返す
スタック検査し
。
動作結果
パーセプトロン数50
NN層1パーセプトロン数 :50 ,SDG ,入力画像数:10000 ,検証画像数:1000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 1回目 誤差エントロピ:1.25626 正解率:0.46500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 2回目 誤差エントロピ:0.89192 正解率:0.61100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 3回目 誤差エントロピ:0.52123 正解率:0.76800
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 4回目 誤差エントロピ:0.40336 正解率:0.82100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 5回目 誤差エントロピ:0.33500 正解率:0.85800
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 6回目 誤差エントロピ:0.33845 正解率:0.85100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 7回目 誤差エントロピ:0.33307 正解率:0.84200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 8回目 誤差エントロピ:0.32488 正解率:0.84900
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 9回目 誤差エントロピ:0.31975 正解率:0.84600
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 10回目 誤差エントロピ:0.32476 正解率:0.84700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 11回目 誤差エントロピ:0.30658 正解率:0.85600
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 12回目 誤差エントロピ:0.31291 正解率:0.85800
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 13回目 誤差エントロピ:0.31719 正解率:0.85400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 14回目 誤差エントロピ:0.32926 正解率:0.85400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 15回目 誤差エントロピ:0.33657 正解率:0.84600
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 16回目 誤差エントロピ:0.33876 正解率:0.84700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 17回目 誤差エントロピ:0.34543 正解率:0.85000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 18回目 誤差エントロピ:0.34533 正解率:0.85200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 19回目 誤差エントロピ:0.35338 正解率:0.85100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 20回目 誤差エントロピ:0.35970 正解率:0.85400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 21回目 誤差エントロピ:0.38479 正解率:0.84400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 22回目 誤差エントロピ:0.37604 正解率:0.84100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 23回目 誤差エントロピ:0.37479 正解率:0.84700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 24回目 誤差エントロピ:0.38147 正解率:0.84200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 25回目 誤差エントロピ:0.40161 正解率:0.84500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 26回目 誤差エントロピ:0.40109 正解率:0.84700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 27回目 誤差エントロピ:0.39734 正解率:0.84500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 28回目 誤差エントロピ:0.41357 正解率:0.83500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 29回目 誤差エントロピ:0.41969 正解率:0.84000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 30回目 誤差エントロピ:0.43215 正解率:0.83900```
パーセプトロン数1024
NN層1パーセプトロン数 :1024 ,SDG ,入力画像数:10000 ,検証画像数:1000
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 1回目 誤差エントロピ:0.30570 正解率:0.86600
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 2回目 誤差エントロピ:0.20524 正解率:0.89500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 3回目 誤差エントロピ:0.17595 正解率:0.89200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 4回目 誤差エントロピ:0.16812 正解率:0.89700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 5回目 誤差エントロピ:0.15982 正解率:0.90200
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 6回目 誤差エントロピ:0.14949 正解率:0.90900
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 7回目 誤差エントロピ:0.14252 正解率:0.91300
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 8回目 誤差エントロピ:0.13654 正解率:0.91700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 9回目 誤差エントロピ:0.13267 正解率:0.92100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 10回目 誤差エントロピ:0.13096 正解率:0.92100
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 11回目 誤差エントロピ:0.13003 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 12回目 誤差エントロピ:0.12951 正解率:0.92500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 13回目 誤差エントロピ:0.12973 正解率:0.92700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 14回目 誤差エントロピ:0.13025 正解率:0.92700
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 15回目 誤差エントロピ:0.13062 正解率:0.92600
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 16回目 誤差エントロピ:0.13097 正解率:0.92600
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 17回目 誤差エントロピ:0.13180 正解率:0.92600
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 18回目 誤差エントロピ:0.13212 正解率:0.92500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 19回目 誤差エントロピ:0.13260 正解率:0.92500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 20回目 誤差エントロピ:0.13309 正解率:0.92500
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 21回目 誤差エントロピ:0.13354 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 22回目 誤差エントロピ:0.13382 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 23回目 誤差エントロピ:0.13429 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 24回目 誤差エントロピ:0.13459 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 25回目 誤差エントロピ:0.13499 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 26回目 誤差エントロピ:0.13524 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 27回目 誤差エントロピ:0.13562 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 28回目 誤差エントロピ:0.13595 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 29回目 誤差エントロピ:0.13616 正解率:0.92400
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
検証 30回目 誤差エントロピ:0.13648 正解率:0.92400
回数を進めると、誤差エントロピが下がっている。
パーセプトロン数が1024の場合には、正解率は92%程度ある。
ニューラルネットワークの学習がうまく機能していると判断します。
計算時間
手元の環境で、
50パーセプトロンの時は 2~3時間、1024パーセプトロンの時は1日程度、要しています。
次記事
Mind で Neural Network (準備編3) 文字画像の読み込みの改良
Mind で Neural Network (adam)