cuBLSA を用いて GPU で 行列の積演算を行わせるにあたり、行列の積演算関数の引き数には、入力行列の転置の指定があり、転置によって計算時間にどう影響あるのか調査しました。
調査結果を公開します。
背景
深層学習の理解を深めようと自前で実装を行っていると、行列の積演算 の所要時間を少しでも短くしようと感じます。
BLASでの計算時間は、いかにメモリアクセスの時間を短縮するかの工夫(キャッシュメモリに当てる、メモリを連続的にアクセスする)の世界になっていると想像し、入力行列の転置によっても、所要時間に影響あるかと予想し、今回測定しました。
行列の積演算関数 gemm()
参照先「cuda tool kit documentation cublasgemm()」
cublasSgemm(
handle,
CUBLAS_OP_N, //行列A 転置有無
CUBLAS_OP_N, //行列B 転置有無
num, // 行列Aの行数
num, // 行列Bの列数
num, // 行列Aの列数(=行列Bの行数)
&alpha, // 行列の積に掛ける値(なければ1)
devA, // 行列A
num, // 行列Aの行数
devB, // 行列B
num, // 行列Bの行数
&beta, // 行列Cに掛けるスカラ値(なければ0)
devC, // 行列Cの初期値 兼 出力先
num // 行列Cの行数
);
↑の 行列A と 行列B の転置有無の引数を、
| 値 | 意味 |
|---|---|
| CUBLAS_OP_N | 転置なし |
| CUBLAS_OP_T | 転置あり |
の 値を指定することで、転置の有無を指定します。
転置による所要時間
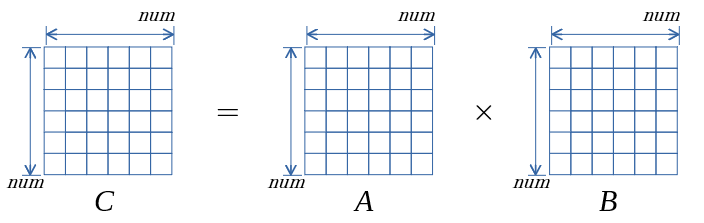
- 一辺 num の 正方行列(下図)で、 num を増やしていった際の 所要時間で比較する。
-
測定は 「転置なし(無印)」「Aのみ転置(At)」「Bのみ転置(Bt)」「A,Bともに転置(AtBt)」の4種
-
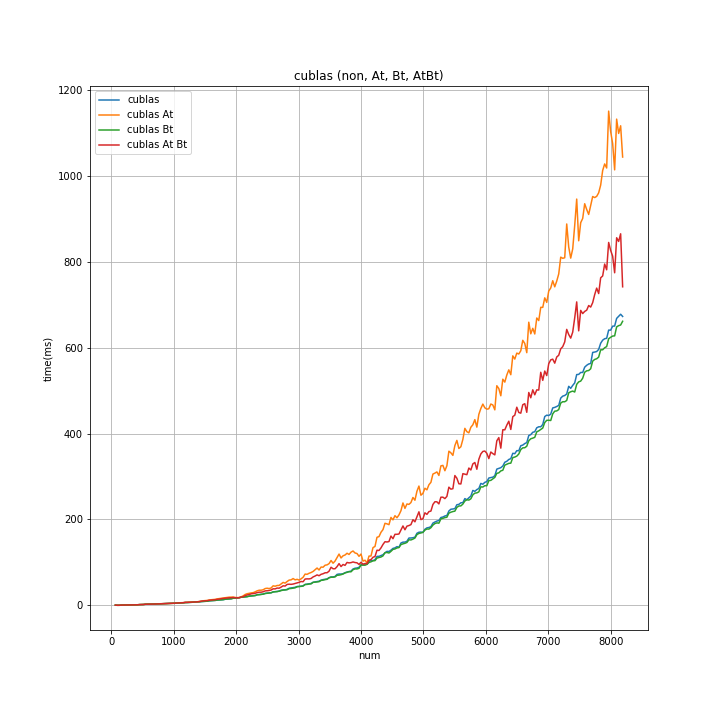
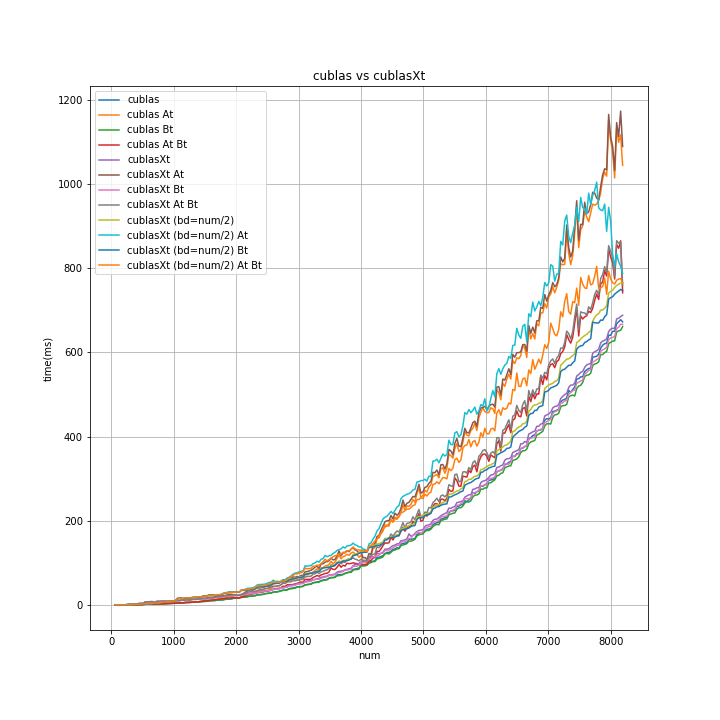
測定は、下記グラフは、前回の記事「cuBLAS と cuBLAS-XT の調査。行列の積演算にて」で有力だった cuBLAS での測定。 cuBLAS-XTを含めたグラフは後述。
-
各num で10回測定し、平均値をプロット。
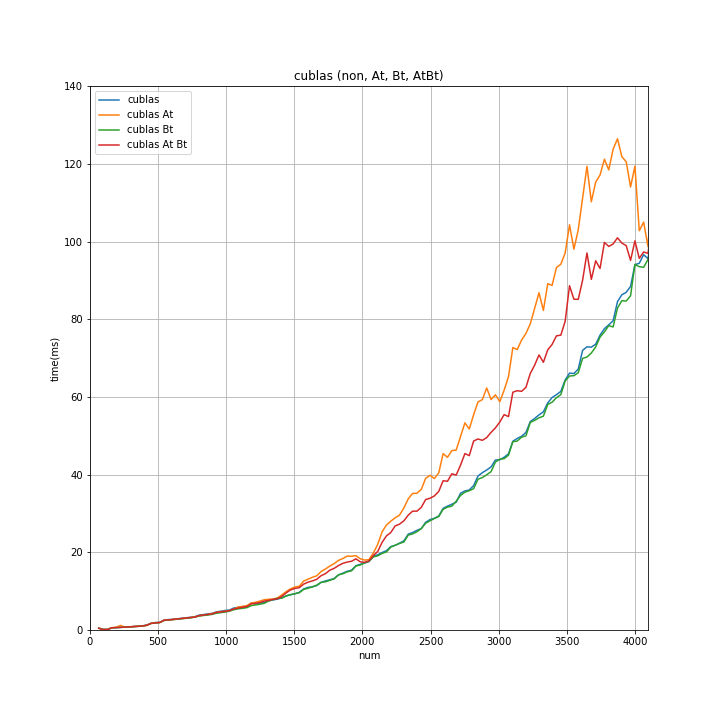
↑を num 4096 以下 で拡大したのが↓
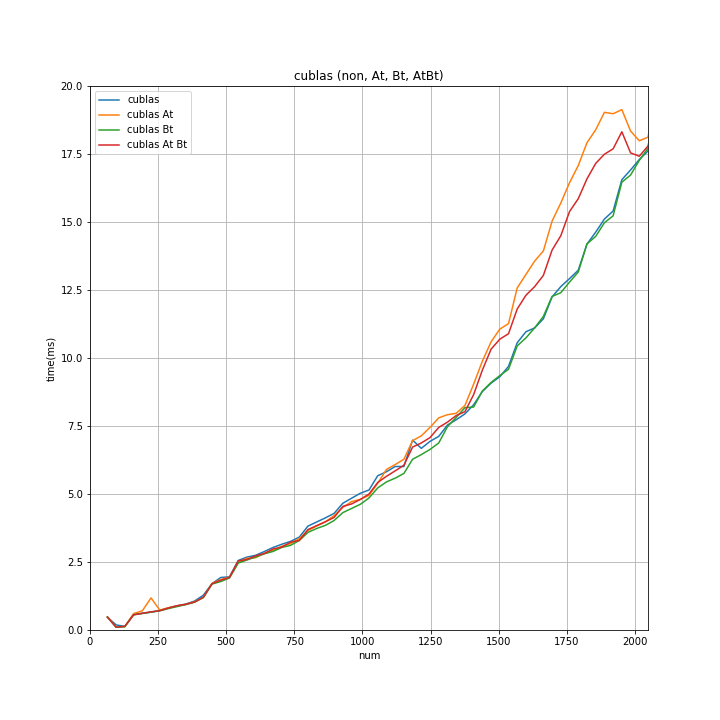
↑を num 2048 以下 で拡大したのが↓
結果
- numの値に関わらず「Bのみ転置」が 所要時間が最も短い。
- 「転置なし」は num が 2000 以下のあたりでは、「Bのみ転置」と同等。numが4096を超えたあたりから ~3%位の差が生じる。
(「転置なし」と「Bのみ転置」間は予想より差が少なかった。「Aのみ転置」と「転置なし」と同様の差が、「転置なし」と「Bのみ転置」間にもあるように予想してました)
→「Bのみ転置」を用いるのが良さそう。
cuBLAS-XT も含めた比較
- 所要時間の短い方から、「cublas(Bのみ転置)」「cublasXt(Bのみ転置)」「cublas(転置なし)」「cublasXt(転置なし)」
- 「Bのみ転置」にしても、cuBLAS-XT より cuBLA のが わずかに所要時間が短い。(グラフィックカードが1枚の場合)
実装の話
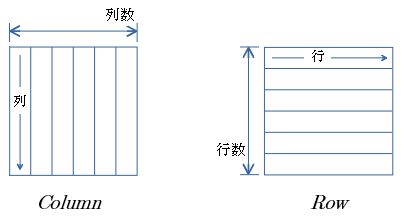
BLASで扱う行列は Column優先(列優先)のメモリ配置。
画像などでよく用いる Row とは向きが異なるので注意が必要。
col優先での B転置!? メモリにどう配置するん?
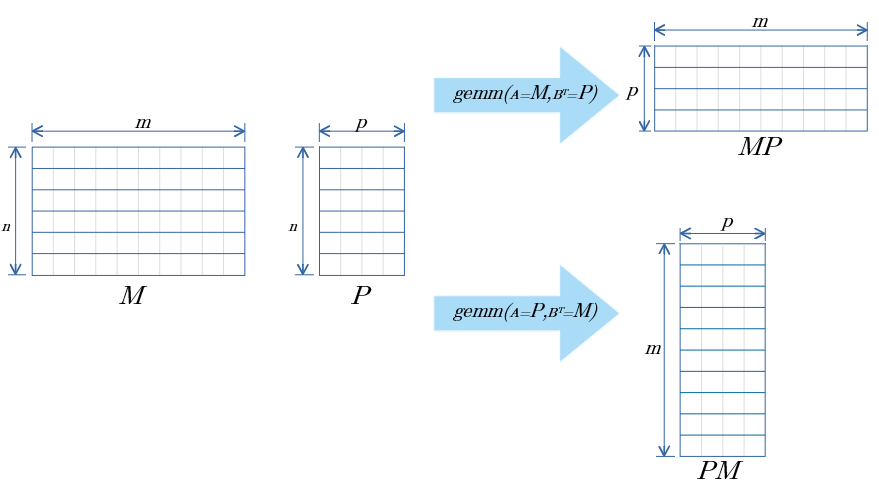
Row 優先表記で↓の配置。
特徴
- MとPの共通項がどちらも 行数 になる。 (どっちがどっちでの悩みが一つ減る)
- MとP、どちらをAにするかで、結果の転置を調整できる。
これはこれで便利そう。 (うまくできてるもんですね)
検算したの?
むしろ、結果から逆算しました...。
入力:
--- M ---
mem:[ 1.0000 ,2.0000 ,3.0000 ,4.0000 ,5.0000 ,6.0000 ,7.0000 ,8.0000 ,9.0000 ]
1.0000 2.0000 3.0000
4.0000 5.0000 6.0000
7.0000 8.0000 9.0000
--- P ---
mem:[ 0.0001 ,0.0010 ,0.0100 ,0.1000 ,1.0000 ,10.0000 ,100.0000 ,1000.0000 ,10000.0000 ]
0.0001 0.0010 0.0100
0.1000 1.0000 10.0000
100.0000 1000.0000 10000.0000
結果:
--- M×Pt ---
mem:[ 700.4001 ,800.5002 ,900.6003 ,7004.0010 ,8005.0020 ,9006.0030 ,70040.0100 ,80050.0200 ,90060.0300 ]
700.4001 800.5002 900.6003
7004.0010 8005.0020 9006.0030
70040.0100 80050.0200 90060.0300
--- P×Mt ---
mem:[700.4001 ,7004.0010 ,70040.0100 ,800.5002 ,8005.0020 ,80050.0200 ,900.6003 ,9006.0030 ,90060.0300 ]
700.4001 7004.0010 70040.0100
800.5002 8005.0020 80050.0200
900.6003 9006.0030 90060.0300