計算グラフ(computational graph)の 基本パーツ の図解です。
ニューラルネットワークの誤差逆伝播法を学習時に 計算グラフを 知りました。
局所的な計算を連鎖させていく考え方で、理解しやすくて良いですね。
計算グラフの基本パーツ
本記事の図では、黒線・黒文字は順伝搬、赤線・赤文字は逆伝播を示します。
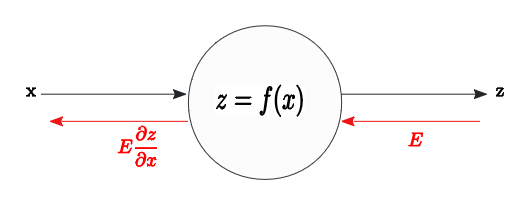
z=f(x)
順方向 z=f(x) の計算の場合、
その逆伝播は 入力値$E$に f(x)の微分値を掛けた値が 出力となる。
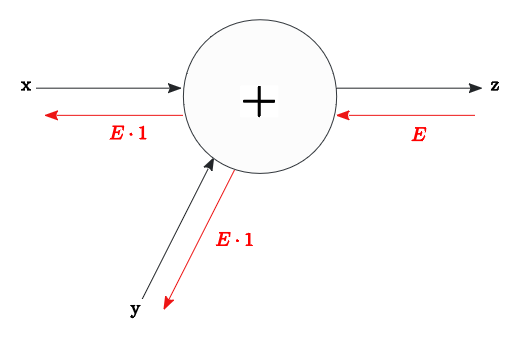
加算ノード
加算ノードの逆伝播は、 入力値$E$ をそのまま 伝達する。
順方向 $z=x+y$ に対し、
$x$ の微分値 $\frac{\partial z} {\partial x}$ は $1$
$y$ の微分値 $\frac{\partial z} {\partial y}$ も $1$
のため、入力$E$ を そのまま伝達 となる。
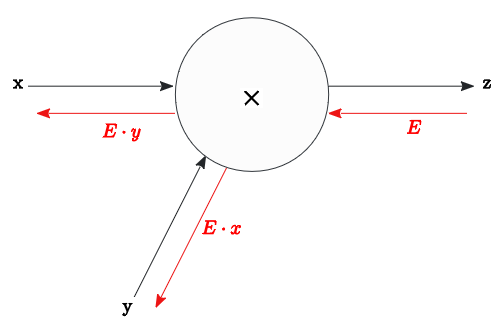
乗算ノード
加算ノードの逆伝播は、 入力値$E$ × 順伝播を入れ替えた値 を伝達する。
順方向 $z=xy$ に対し、
$x$ の微分値 $\frac{\partial z} {\partial x}$ は $y$
$y$ の微分値 $\frac{\partial z} {\partial y}$ は $x$
のため、入力値$E$ × 順伝播を入れ替えた値を 伝達となる。
分岐ノード
順伝播の式中の２か所で $x$が参照されている場合に、$x$の分岐と扱う。
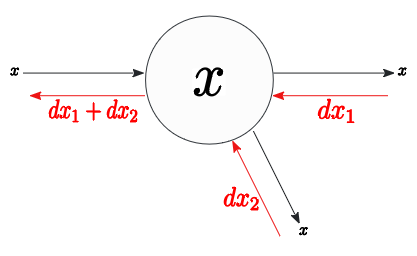
逆伝播は、分岐先からの逆伝播値の和 を伝達する。
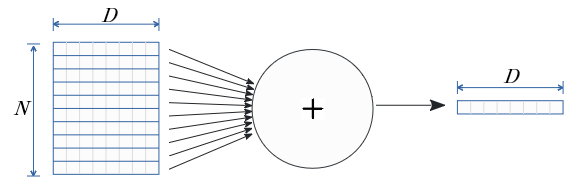
総和ノード
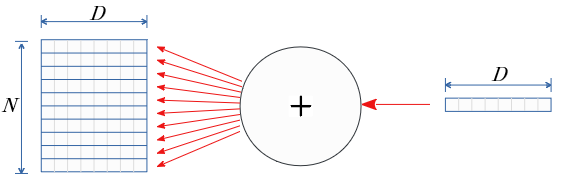
伝播する行列での一方向で(下図の例では$N$の方向で)総和を求める場合、(N,D)の行列は (D,)の次元になる。
総和は 下図の様に 多数の加算ノード と読みかえ出来る。
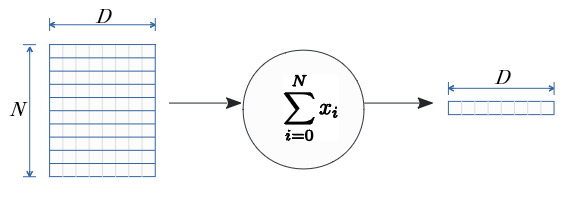
総和の逆伝播は、(D,)次元の逆伝播の入力行列を、そのまま$N$個に伝達し(N,D)次元の行列を生成する。
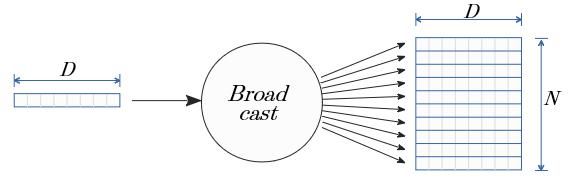
Broadcast ノード
行列のアダマール積にて
(N,D)次元の行列A と (D,)次元の行列Bの積を求める場合、Bは下図で示す Broadcast が行われ(N,D)次元の行列として演算する。
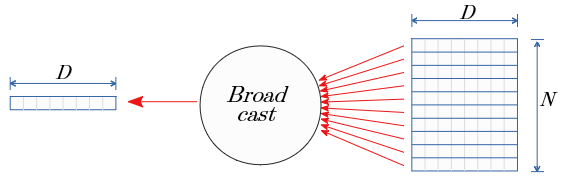
Broadcastは N個への分岐ノードと読みかえが出来る。
逆伝播は、(N,D)次元の行列から (D,)次元への 総和となる。
