行列の積演算をNVIDIAのGPUで行わせたく、CUDA 内の cuBLAS のドキュメントを読み進めたところ、cuBLAS-XT 推しな記述が目に留まり、自分の用途には cuBLAS と cuBLAS-XT のどちらが適しているかの観点で調査を行いました。
内容を公開します。
背景
深層学習の理解を深めようと自前で実装を行っていると、行列の積演算を高速化したくなるかと思います。(なりました)
GPUを用いての行列の積演算 を行うにはどれ位の学習コストがかかるかの調査のつもりが、cuBLASのサンプルプログラムをみると、簡単そうに見え、まず使ってみてから、引っかかった所を調べてく方が効率よさそうに思え、調べた内容が本記事です。
cuBLAS-XT
- cuBLAS-XT は、行列の積演算を含むBLASのLv3関数を、複数のGPUカードで分散・並列して行わせる事が可能なことが特徴です。
ソースを見て頂いてからの方が話が早そうなので、cuda Tool Kit サンプルプログラムをもとに作成した、cuBLAS と cuBLAS-XT の 正方行列の時間測定ルーチンの抜粋を掲載します。(エラー処理系は省略してます)
//抜粋
// 所要時間測定用
timeval st,et;
//ホスト側用
float *hstA,*hstB,*hstC;
//デバイス(GPU)側用
float *devA,*devB,*devC;
// 行列演算 C=αAB+βC のパラメータ
float alpha = 1.0f;
float beta = 0.0f;
// 正方行列 A B C の 一辺のサイズ
int num = 8192; //例
//メモリサイズ算出
int n2 = num*num;
size_t memSz = n2 * sizeof(float);
//ホスト側メモリ確保
hstA=(float*)malloc(msmSz);
hstB=(float*)malloc(msmSz);
hstC=(float*)malloc(msmSz);
// hstA,hstB に値を入れる。略
// 計測開始点
gettimeofday(&st,NULL);
//デバイス側メモリ確保
cudaMalloc((void **)&devA,memSz);
cudaMalloc((void **)&devB,memSz);
cudaMalloc((void **)&devC,memSz);
//ホスト → デバイス memcpy
cublasSetVector(n2, sizeof(float), hstA, 1, devA, 1);
cublasSetVector(n2, sizeof(float), hstB, 1, devB, 1);
// デバイス側ハンドル作成
cublasHandle_t handle;
cublasCreate(&handle);
// 行列の積 演算
cublasSgemm(
handle,
CUBLAS_OP_N, //行列A 転置有無
CUBLAS_OP_N, //行列B 転置有無
num, // 行列Aの行数
num, // 行列Bの列数
num, // 行列Aの列数(=行列Bの行数)
&alpha, // 行列の積に掛ける値(なければ1)
devA, // 行列A
num, // 行列Aの行数
devB, // 行列B
num, // 行列Bの行数
&beta, // 行列Cに掛けるスカラ値(なければ0)
devC, // 行列Cの初期値 兼 出力先
num // 行列Cの行数
);
// デバイス側ハンドル破棄
status = cublasDestroy(handle);
// ホスト ← デバイス memcpy (計算結果取得)
cublasGetVector(n2, sizeof(float), devC, 1, hstC, 1);
// デバイス側メモリ解放
cudaFree(devA);
cudaFree(devB);
cudaFree(devC);
// 計測終了点
gettimeofday(&et,NULL);
// ホスト側メモリ解放
free(hstA);
free(hstB);
free(hstC);
↑ の cuBLAS での 行列の積演算の使い方でも、身構えてたよりは、随分と簡単に使えて驚いたのですが...
↓ の cuBLAS-XT では、さらに、簡略化できます。
//抜粋
// 所要時間測定用
timeval st,et;
//ホスト側用
float *hstA,*hstB,*hstC;
//デバイス(GPU)側用
//
// 行列演算 C=αAB+βC のパラメータ
float alpha = 1.0f;
float beta = 0.0f;
// 正方行列 A B C の 一辺のサイズ
int num = 8192; //例
//メモリサイズ算出
int n2 = num*num;
size_t memSz = n2 * sizeof(float);
//ホスト側メモリ確保
hstA=(float*)malloc(msmSz);
hstB=(float*)malloc(msmSz);
hstC=(float*)malloc(msmSz);
// hstA,hstB に値を入れる。略
// 計測開始点
gettimeofday(&st,NULL);
//デバイス側メモリ確保
//
//ホスト → デバイス memcpy
//
// デバイス側ハンドル作成
cublasXtHandle_t handle;
cublasXtCreate(&handle);
// デバイス選択
int devices[1] = {0};
cublasXtDeviceSelect(handle, 1, devices);
// 分割ブロックの一辺のサイズ
int cub=num; // 分割なしの例
cublasXtSetBlockDim(handle, cub);
// 行列の積 演算
cublasXtSgemm(
handle,
CUBLAS_OP_N, //行列A 転置有無
CUBLAS_OP_N, //行列B 転置有無
num, // 行列Aの行数
num, // 行列Bの列数
num, // 行列Aの列数(=行列Bの行数)
&alpha, // 行列の積に掛ける値(なければ1)
hstA, // 行列A
num, // 行列Aの行数
hstB, // 行列B
num, // 行列Bの行数
&beta, // 行列Cに掛けるスカラ値(なければ0)
hstC, // 行列Cの初期値 兼 出力先
num // 行列Cの行数
);
// デバイス側ハンドル破棄
status = cublasXtDestroy(handle);
// ホスト ← デバイス memcpy (計算結果取得)
//
// デバイス側メモリ解放
//
// 計測終了点
gettimeofday(&et,NULL);
// ホスト側メモリ解放
free(hstA);
free(hstB);
free(hstC);
デバイス(GPU)側メモリ確保・転送・解放の隠蔽化
- cuBLAS は GPU側のメモリ確保、ホストとGPU間のメモリコピー、GPU側のメモリ解放、を明記する。
- cuBLAS-XT では、GPU側のメモリ確保、ホストとGPU間のメモリコピー、GPU側のメモリ解放、を明記しなくてもよい。
- cuBLAS-XT では、複数のグラフィックカードのGPUに、分散・並列しての計算を可能とするため、各カードのGPUのメモリ確保や転送やメモリ解放の処理を隠蔽してくれたと解釈しています。
- cuBLAS-XT でも、cuBLASと同様に GPU上に自前で確保したメモリを用いての演算も可能です。
(ある演算結果を次の演算の入力に使いたい等、GPU上での演算を連続して行わせる事も可能です)
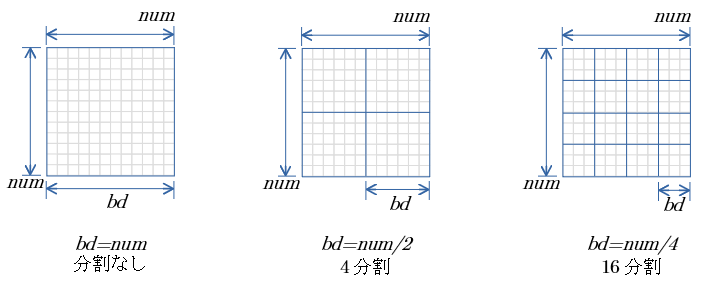
ブロック分割
cuBLAS-XT では cuBLASと同じ引数の関数から、行列の積演算を複数のグラフィックカードに分散させ並列で演算させることが可能です。
分散させる単位は 関数:
cublasXtSetBlockDim(ハンドル, 分割ブロックの1辺サイズ)
で指定可能です。
NVIDIA Visual Profiler を用いて、行列の積演算の流れを見ます
- num=8192 の正方行列の積
- cuBLAS , cuBLAS-XT で bd を 8192(分割なし), 4096(4分割), 2048(16分割) の4処理 の結果を示します。
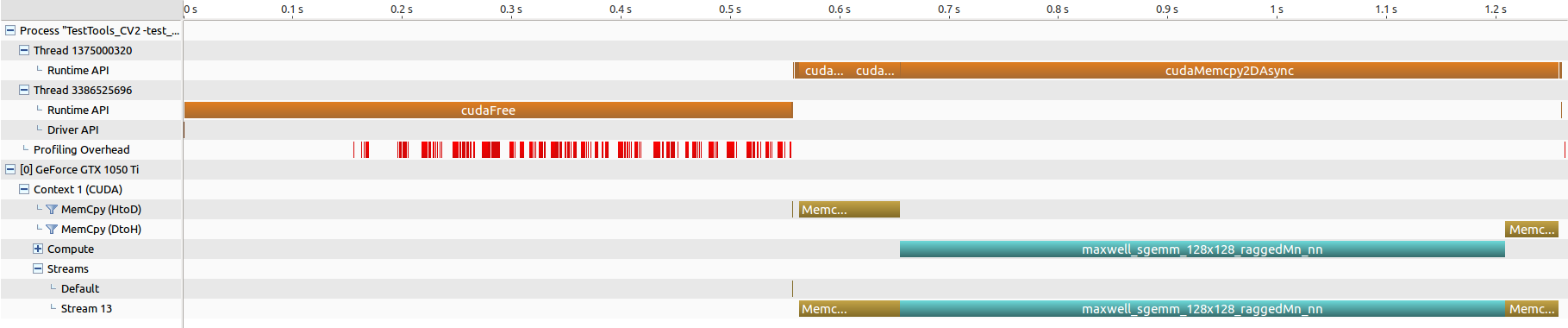
cuBLAS num=8192
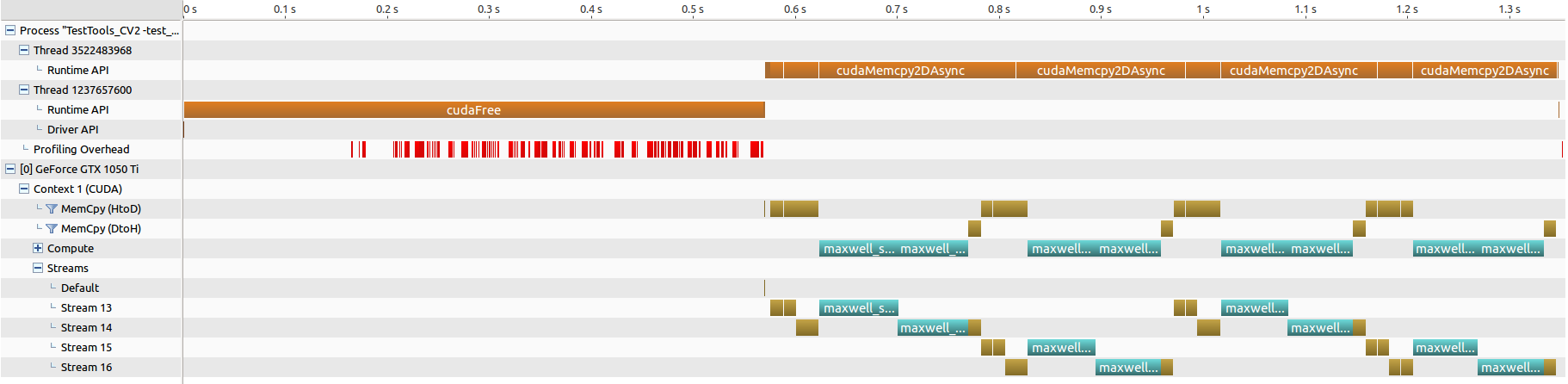
cuBLAS-XT num=8192, bd=8192 (分割なし)
cuBLAS-XT num=8192, bd=4096 (4分割)
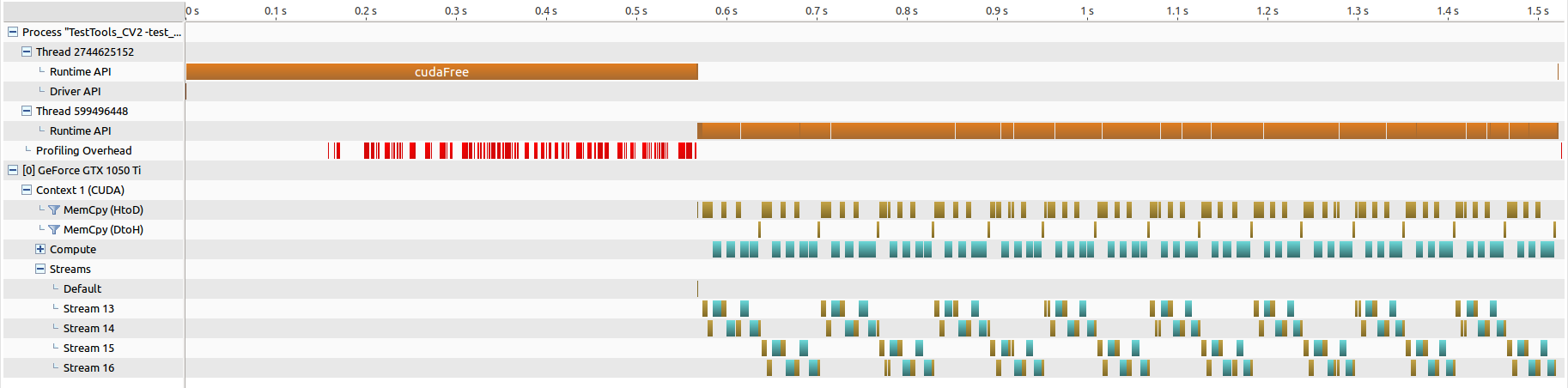
cuBLAS-XT num=8192, bd=2048 (16分割)
- 手元の環境は、グラフィックカードが一枚のみ。
- ブロック分割は行われている様ですが、ブロック単位での並列化は行えてなく、所要時間の短縮とはなってません。
- グラフィックカードが複数枚ある環境の結果も見てみたい……。(チラッ
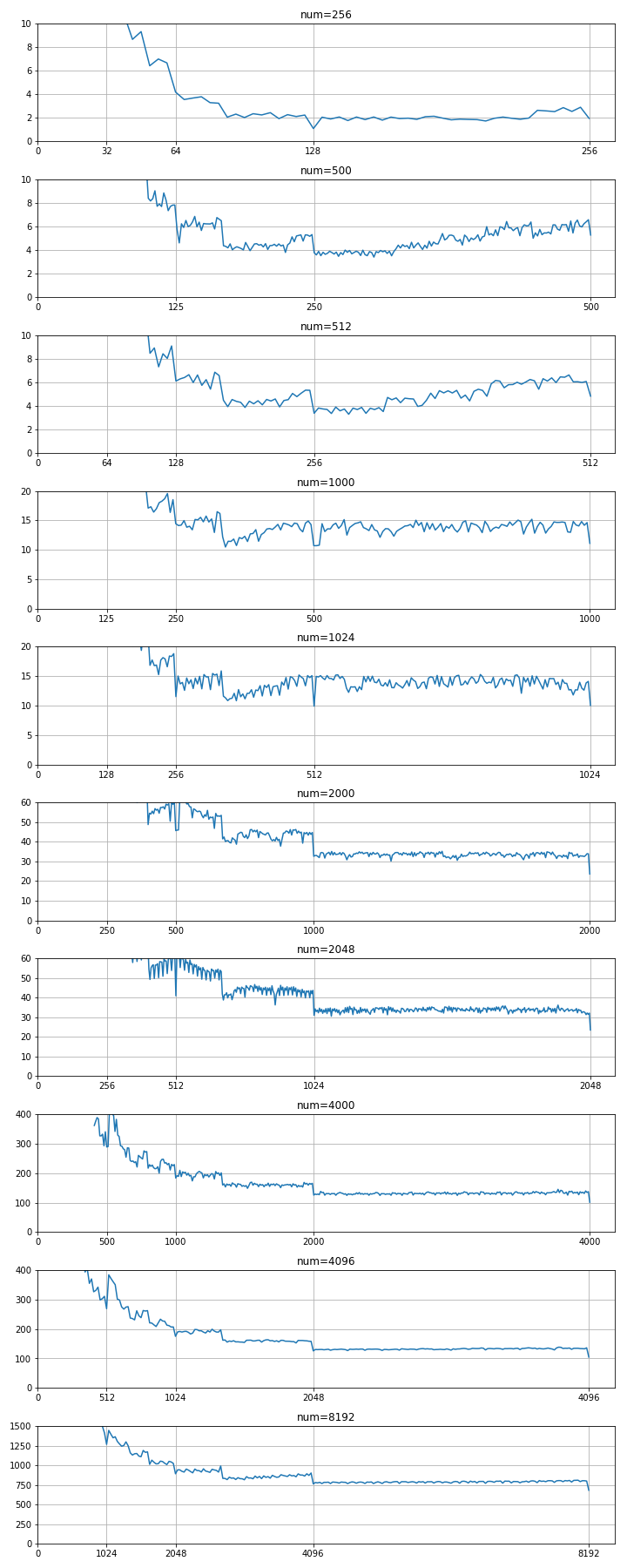
分割ブロックの一辺サイズ(bd)による 所要時間比較
- num=256, 500, 512, 1000, 1024, 2000, 2048, 4000, 4096 , 8000 とし num値の違いで傾向の違いがあるか見ました。
- 上記numの正方行列で、bd の値を変えていき、行列の積 演算 の所要時間を測定。
- 各bdにつき 10回施行し 平均値をプロット。
- 測定環境については 前記事( 行列の積演算で openBLAS cuBLAS を体感する )を参照。
- グラフは下側が良く(所要時間が短い)、上側に行くほど悪い(所要時間が長い)。
- 1000と1024の間、2000と2048の間、4000と4096の間で、極端な違いはない。numが2の乗数の時に特別速くなる等の事象を期待していたが、そんな傾向はなさそう。
- bd にマジックナンバーのような、特別速くなる値は存在しなさそう。
- num が1024 以下の時は、bd=num/2 (4分割) が 最短所要時間。 グラフィックカードが1枚でも、numの値によっては、分割した方が速い場合があることを確認しました。
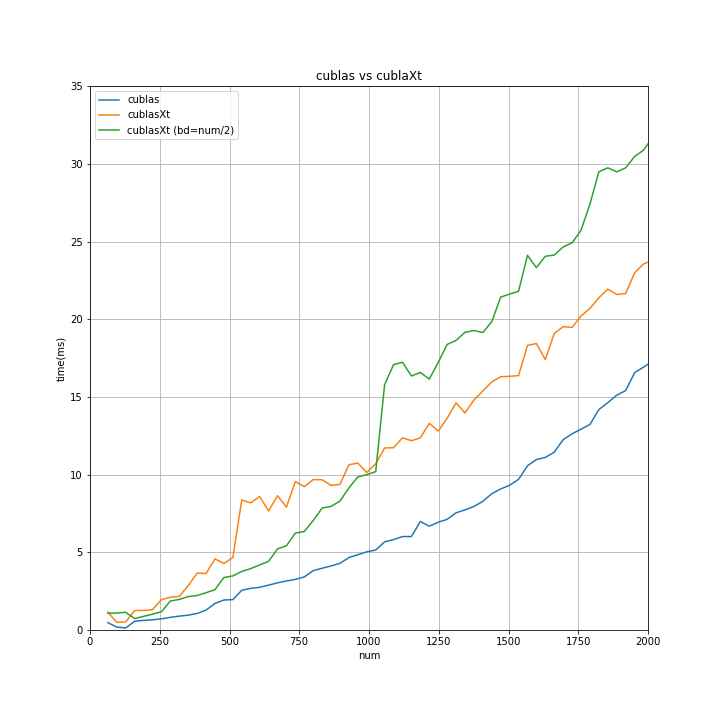
cuBLAS と cuBLAS-XT(分割なし,4分割) で 所要時間比較
- cuBLAS と cuBLAS-XT(分割なし) と cuBLAS-XT(4分割) で 比較する。
- num の値を変えていき、正方行列の 行列の積演算の 所要時間を比較する。
- 各num につき 10回施行し 平均値をプロット。
- グラフは下側が良く(所要時間が短い)、上側に行くほど悪い(所要時間が長い)。
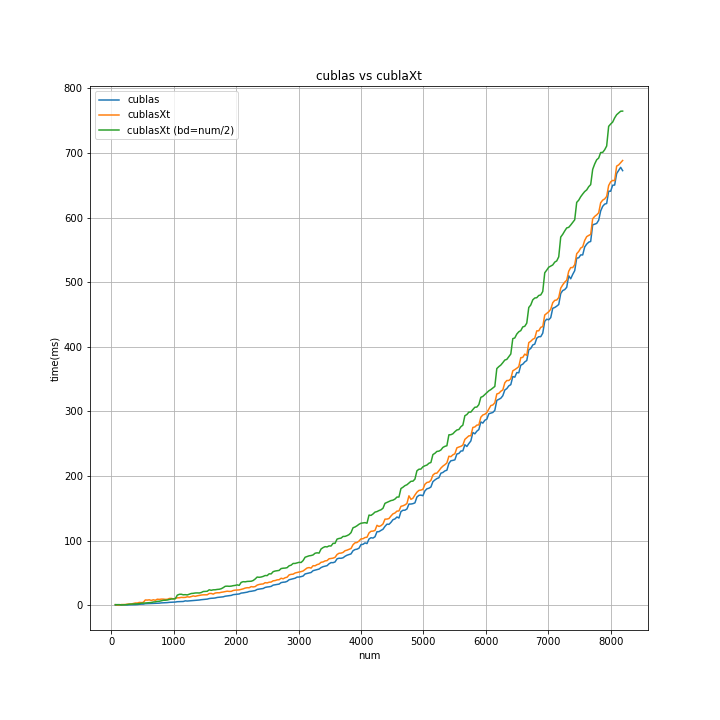
↑を拡大したのが↓
ぁ......。
グラフィックカードが1枚な、うちの環境では、cuBLAS を使った方がよさそう...ですね。
グラフィックカード複数枚の環境下で動かすことを視野に入れるなら、cuBLAS-XTで実装しとくのも...アリですね。
次回
col 優先 と C メモリ配置と、入力行列 A B の転置での 処理時間についての 調査結果の記事です。
→「cuBLAS と cuBLAS-XT の調査(その2)。行列の積演算にて。転置の影響。」