LoginSignup
13
1
@t-shiroganein株式会社セレス

某お遊戯場の確率をPythonを使って検証してみよう

Last updated at Posted at 2023-11-29

某お遊戯場の確率をPythonを使って検証してみよう

某お遊技場で一般的な1/319を引くためには何回の試行が必要か気になったことはありませんか？ありますよね。そうですよね。

今回はPythonを使用して、1/319引くためには大体どのくらいの試行が必要かを検証していきながら、Pythonに対する理解も合わせて深めていければいいなと思っています

今回の要件

  • 当たりの確率を1/319とする
    • 内部的には205/65536として認識している説がありますので今回はこれを採用します.

  • 試行ごとに抽選はリセットします
    • ※この構造が正しいかはわからないです。色々検証していく中で一番しっくりきたので、これを採用しました

  • お遊技場を模して、仮想の単位xymを使用して試行回数を見ていきます
    • 500xymで0回から18回の試行を可能とします
    • 最終的にxymがいくつ必要になったかを確認します

  • 最後に当たりを引くために必要とした試行回数とxymの消費量について、最大値と最小値そして平均を求めます。

環境

$ python3 -V
Python 3.11.2

今回使うモジュールはrandomとmathとmatplotlibです。
randomとmathに関しては3.11.2では標準でインストールされていますので、追加のインストールは不要です。

最後にグラフ表示するのにmatplotlibを使用しています。
入ってない場合はインストールしておいてください。

$ python3 -m pip install matplotlib

書いていく

当たりの確率を1/319とする

当たりの確率を1/319としましょう。
今回キモとなるのがrandom.getrandbits(16)
16bitの最大値(65536)の中からランダムの数値を返してくれるというもの
今回はこれを主軸にして書いていきます。


# モジュールのインポート
import random

# 変数の定義
hit_value = []
# 当たりの確率 205/65536
hit_count = 205

# 当たりとなる数値を65536の中から205個ランダムに選出
while hit_count > 0:
    hit_value.append(random.getrandbits(16))
    hit_count -= 1

# 抽選に挑戦する数値を定義
try_value = random.getrandbits(16)            

# 挑戦した数値が当選番号として存在するか確認します
if try_value in hit_value:
    print("hit!")
else:
    print("NG!")

さすがに単発で当たるまで試行するのは骨が折れるので、当たるまで試行してみましょう
ついでに試行回数も記録するようにしちゃいましょう

# モジュールのインポート
import random

# 変数の定義
hit_value = []
# 当たりの確率 205/65536
hit_count = 205
# 試行回数を定義しておく
trials = 0
# 繰り返しフラグを定義しておく
flag = False

# 当たりとなる数値を65536の中から205個ランダムに選出
while hit_count > 0:
    hit_value.append(random.getrandbits(16))
    hit_count -= 1

# flagがFalseの場合繰り返し
while not flag:
    # 試行回数を増やす
    trials += 1

    # 抽選に挑戦する数値を定義します
    try_value = random.getrandbits(16)            

    # 挑戦した数値が当選番号として存在するか確認します
    if try_value in hit_value:
        print("hit!" + str(try_value) + " try_count " + str(trials))
        # 繰り返しを終了させる
        flag = True
    else:
        print("NG!" + str(try_value) + " try_count " + str(trials))

今回は21856という数値で当たったみたいですね
これで当たりのチェックと試行回数のカウントについては大丈夫そうですね

$ python3 main.py
--snip--
NG!42663 try_count 795
NG!33144 try_count 796
NG!52453 try_count 797
NG!54089 try_count 798
NG!48990 try_count 799
NG!33284 try_count 800
NG!11226 try_count 801
NG!31992 try_count 802
NG!56981 try_count 803
NG!29157 try_count 804
NG!25896 try_count 805
NG!58202 try_count 806
NG!23601 try_count 807
NG!32658 try_count 808
NG!49276 try_count 809
NG!38269 try_count 810
NG!45216 try_count 811
NG!53218 try_count 812
NG!6286 try_count 813
NG!23746 try_count 814
hit!21856 try_count 815

試行ごとに抽選はリセットします

毎回当たりとなる数値は定義し直すようにしましょう
当選番号を定義するwhile文を試行するwhile文の中に入れだけです
これで試行の都度、当選番号を定義し直す処理に変わりました


# モジュールのインポート
import random

# 変数の定義
hit_value = []
# 当たりの確率 205/65536
hit_count = 205
# 試行回数を定義しておく
trials = 0
# 繰り返しフラグを定義しておく
flag = False


# flagがFalseの場合繰り返し
while not flag:
    # 試行回数を増やす
    trials += 1
    # 当たりとなる数値を65536の中から205個ランダムに選出
    while hit_count > 0:
        hit_value.append(random.getrandbits(16))
        hit_count -= 1

    # 抽選に挑戦する数値を定義
    try_value = random.getrandbits(16)            

    # 挑戦した数値が当選番号として存在するか確認します
    if try_value in hit_value:
        print("hit!" + str(try_value) + " try_count " + str(trials))
        # 繰り返しを終了させる
        flag = True
    else:
        print("NG!" + str(try_value) + " try_count " + str(trials))

500xymで0回から18回の試行を可能とします

当選するまでの必要な試行回数に応じて500xym加算されていく処理を追加しましょう
さらに、random.randint(0, 18)を使用して0から18の数値からランダムな数値を取得しましょう

# モジュールのインポート
import random

# 全体の試行回数
try_count = 100

# 結果を入れる箱を用意
result_trials = []
result_xym = []

# 全体の試行回数がなくなるまで繰り返し
while try_count > 0:
    # 繰り返しフラグを定義
    flag = False
    
    # 初期化 
    xym = 0
    trials = 0

    # フラグが立たない限り繰り返し
    while not flag :
        # 500xymの試行回数を決定
        plays_per_count = random.randint(0, 18)
        # 500xymの加算
        xym += 500

        # 定義された回数分だけ試行
        while plays_per_count > 0:
            # 試行回数を増やす
            trials += 1
            # 当たりの数値を入れる箱を用意
            hit = []
            # 当たり確率 205/65536
            hit_count = 205


            # 当たりとなる数値を65536の中から205個ランダムに選出
            while hit_count > 0:
                hit.append(random.getrandbits(16))
                hit_count -= 1

            # 抽選に挑戦する数値を定義
            value = random.getrandbits(16)

            # 挑戦した数値が当選番号として存在するか確認します
            if value in hit:
                # 当選していたら当選した時の状態をresultの箱に保存します
                result_trials.append(trials)
                result_xym.append(xym)
                # 繰り返しから抜けます
                flag = True
                break
            
            # 500xymで決定した試行回数を減らします。なくなったら再度500xymを追加して試行回数から再抽選します
            plays_per_count -= 1
    # 全体の試行回数を減らします
    try_count -= 1

最後に検証結果を出力しましょう

シンプルに端数を切り上げたいのでmathを使用します。

# モジュールのインポート
import random,math

# 全体の試行回数
try_count = 100

# 結果を入れる箱を用意
result_trials = []
result_xym = []

# 全体の試行回数がなくなるまで繰り返し
while try_count > 0:
    # 繰り返しフラグを定義
    flag = False
    
    # 初期化 
    xym = 0
    trials = 0

    # フラグが立たない限り繰り返し
    while not flag :
        # 500xymの試行回数を決定
        plays_per_count = random.randint(0, 18)
        # 500xymの加算
        xym += 500

        # 定義された回数分だけ試行
        while plays_per_count > 0:
            # 試行回数を増やす
            trials += 1
            # 当たりの数値を入れる箱を用意
            hit = []
            # 当たり確率 205/65536
            hit_count = 205


            # 当たりとなる数値を65536の中から205個ランダムに選出
            while hit_count > 0:
                hit.append(random.getrandbits(16))
                hit_count -= 1

            # 抽選に挑戦する数値を定義
            value = random.getrandbits(16)

            # 挑戦した数値が当選番号として存在するか確認します
            if value in hit:
                # 当選していたら当選した時の状態をresultの箱に保存します
                result_trials.append(trials)
                result_xym.append(xym)
                # 繰り返しから抜けます
                flag = True
                break
            
            # 500xymで決定した試行回数を減らします。なくなったら再度500xymを追加して試行回数から再抽選します
            plays_per_count -= 1
    # 全体の試行回数を減らします
    try_count -= 1


# 結果を出力します
print("average_count:" + str(math.ceil(sum(result_trials) / len(result_trials))) + " average_xym:" + str(math.ceil(sum(result_xym) / len(result_xym))))
print("max_count:" + str(max(result_trials)) + " max_xym:" + str(max(result_xym)))
print("min_count:" + str(min(result_trials)) + " min_xym:" + str(min(result_xym)))

これで全ての要件を満たせました！実際に動かしてみましょう!
期待？？してる値が出てますね

$ python main.py 
average_count:355 average_xym:20025
max_count:1607 max_xym:95500
min_count:1 min_xym:500

トータルの回数を増やしてグラフで表示してみましょう

# モジュールのインポート
import random,math
import matplotlib.pyplot as plt

# 全体の試行回数
try_count = 5000

# 結果を入れる箱を用意
result_trials = []
result_xym = []

# 全体の試行回数がなくなるまで繰り返し
while try_count > 0:
    # 繰り返しフラグを定義
    flag = False
    
    # 初期化 
    xym = 0
    trials = 0

    # フラグが立たない限り繰り返し
    while not flag :
        # 500xymの試行回数を決定
        plays_per_count = random.randint(0, 18)
        # 500xymの加算
        xym += 500

        # 定義された回数分だけ試行
        while plays_per_count > 0:
            # 試行回数を増やす
            trials += 1
            # 当たりの数値を入れる箱を用意
            hit = []
            # 当たり確率 205/65536
            hit_count = 205


            # 当たりとなる数値を65536の中から205個ランダムに選出
            while hit_count > 0:
                hit.append(random.getrandbits(16))
                hit_count -= 1

            # 抽選に挑戦する数値を定義
            value = random.getrandbits(16)

            # 挑戦した数値が当選番号として存在するか確認します
            if value in hit:
                # 当選していたら当選した時の状態をresultの箱に保存します
                result_trials.append(trials)
                result_xym.append(xym)
                # 繰り返しから抜けます
                flag = True
                break
            
            # 500xymで決定した試行回数を減らします。なくなったら再度500xymを追加して試行回数から再抽選します
            plays_per_count -= 1
    # 全体の試行回数を減らします
    try_count -= 1


# 結果を出力します
# print("average_count:" + str(math.ceil(sum(result_trials) / len(result_trials))) + " average_xym:" + str(math.ceil(sum(result_xym) / len(result_xym))))
# print("max_count:" + str(max(result_trials)) + " max_xym:" + str(max(result_xym)))
# print("min_count:" + str(min(result_trials)) + " min_xym:" + str(min(result_xym)))

# グラフに入れる変数を定義
x = []
y = []


# 配列の中でユニークな値とその値をカウントしてグラフ用の配列へ追加
for hit_number in sorted(set(result_trials)):
    x.append(hit_number) 
    y.append(result_trials.count(hit_number))

# 二つの線を描画
plt.plot(x, y, label='Line', marker='o')

# グラフを表示
plt.show()

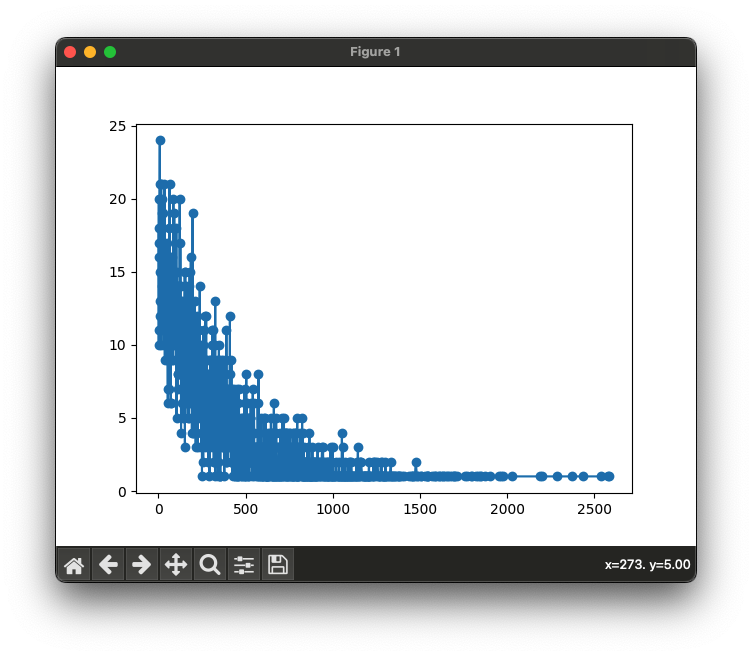
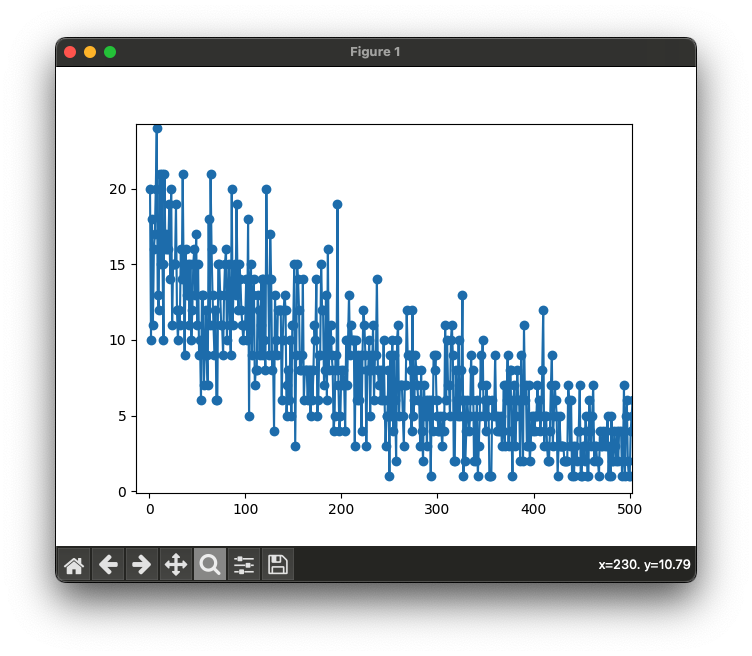
今回の結果はこんな感じで表示されました
案外、早い段階で当たり引けてることが多いみたいですね
スクリーンショット 2023-11-28 20.07.23.png
スクリーンショット 2023-11-28 20.07.34.png

まとめ

いかがだったでしょうか。
みなさんも気になっていたであろう、某お遊技場の確率を実証してみました。
詳しいロジックの部分は完全に同じではないと思いますが、参考値として色々試してみるのもありかもしれません。
ぜひ、遊んでみてください。

13
1
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
13
1