openEMS の存在を最近知りました
電磁界解析のシミュレータってやっぱり特殊用途なので商用のを買うとかなり高額じゃないですか。しかも計算時間も結構かかることが多いのでライセンスも不足しがちだし。オープンで使えるものあったらなーと思っていたんですが、最近 openEMS ってのがあることを知って、ちょっと試してみようと思ったわけです。
まずはインストールですが、公式サイトの手順で問題なくいったので、特にここで記すことはありません。私の環境は Linux Mint22 ですけど、Debian, Ubuntu 系なら問題ないでしょう。一部インストールパッケージの名前が違ったり(libvtk7 が libvtk9 だったり)とかありましたけど、予想の範囲で対処できると思います。Windows はビルド済みバイナリがあるようなのでそれも良いかと思います。試してはいないけど。
解析手法は FDTD法で、手法としてはこなれてると思うんですが、Tutorial 見ると、単なる導波管の素管とか、コレできてもなーって感じのやつしかないので、もうちょっと実用的というか、回路設計してるって感じのやつで試してみようかと考えたわけです。
何を題材にためしてみる?
ただ、解析のためのモデルを用意するのがかなりの重荷なのです。商用ソフトなら、そこはちゃんとした GUI が用意されていて、3D 形状描いてやればいいんでしょうけど、openEMS の場合は、基本コマンドベースで形状定義してやらないといけないみたい(FreeCAD からの変換なんてのもあるみたいだけど)。
そこで、形状が単純で、かつ回路的に応用が効いて、それなりに結果がわかっているものとして、導波管 Band Pass Filter (BPF) のシミュレーションをしてみることにしました。
導波管 BPF の設計手法
一応、導波管 BPF の設計手法について説明しておきますが、かなり端折った説明になってるので、詳細が必要なら文献とかあたってください。まあ、ちゃんと設計したものをシミュレーションしてみたってことで。
管内波長の 1/2 の導波路は、共振周波数付近では LC 共振器っぽく見えます。これを使って BPF を作ります。

BPF の構成はこんな感じで、1/2 波長共振器間を k-inverter で結合します。

k-inverter はこんな回路です。正負のインダクタンスが T型に接続されたものです。
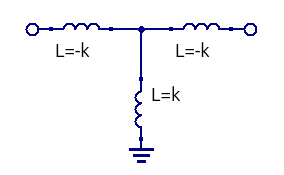
じゃあ k-inverter をどうやって実現するかって話ですが、導波管の中に図のような金属壁を作ると、k-inverter と同等の特性が得られます。

というわけで、BPF の設計のためには、必要な k の値と、それに対応する金属壁の幅の関係を把握しておく必要があります。金属壁の幅と k の値との関係は、論理計算で求める方法もあるし、シミュレーションで解析的に求めることもできますが、ここでは詳細は省きます。(加えて、k-inverter の計算を行う際には、そこに接続される前後の導波路の長さも変わるので、その量も把握しておく必要があります。)
k の値はどうやって決まる?
通過周波数を f1 から f2、導波路の特性インピーダンスを Z0 として、
$$ f_{BW} = \frac{f_2 - f_1}{\sqrt{f_1 f_2}} , \quad \omega_0 = 2 \pi \sqrt{f_1 f_2} $$
これらを用いて、各 k-inverter の値は以下で決定できます。
$$ K_{0,1} = K_{n,n+1} = \sqrt{\frac{Z_0 f_{BW} L_0}{\omega_0 g_1}} , \quad K_{i,i+1} = \frac{f_{BW} L_0}{\sqrt{g_i g_{i+1}}} , (i=1,2 \ldots n-1) $$
ここで gn はチェビシェフ多項式ってやつで、以下のような数式で計算できるものです。(Rdb は帯域内の許容偏差量)
$$ g_1 = \frac{2 a_1}{Y} , \quad g_k = \frac{4 a_{k-1} a_k}{b_{k-1} g_{k-1}} $$
$$ a_k = \sin \left( \frac{(2k-1)\pi}{2n} \right) , \quad b_k = Y^2 + \sin^2 \left( \frac{k\pi}{n} \right) , \quad Y = \sinh \left( \frac{\ln \left( \coth \left( \frac{R_{dB} \ln(10)}{40} \right) \right)}{2n} \right) $$
というわけで、適当な条件で設計してみました。
導波管のサイズは 5.6mm x 2.8mm (WR-22相当)で、通過周波数を 39.5〜40.5 GHz。金属壁の厚さを 200um とし、共振器 5段として、結局こんなのが設計できました。
各部の寸法は、d1=0.3mm, d2=2.0mm, d3=2.425mm, L1=3.855mm, L2=3.88mm, L3=3.885mm で、左右対称です。
実際にモノとして作る場合は、この図のような厚さ 200um の金属板を作成し、両側から凹型の金属ブロックで挟むと導波管 BPF が実現できます。
Python スクリプト
こんなスクリプトで openEMS をキックします。元になっているのは Rectangular Waveguide の Tutorials で、AddMetal で金属壁を追加しただけです。メッシュサイズはデフォルトで 100um ですが(コマンドラインから指定可)、z 方向のみ、金属壁構造がメッシュにうまくのるように微調整しています。(SmoothMeshLines とか使ったほうがいいのかしらん?この辺はまだよくわかってない。)
#!/usr/bin/env python
import sys
import os
import numpy as np
from CSXCAD import ContinuousStructure
from openEMS import openEMS
from openEMS.physical_constants import *
# デフォルトのメッシュサイズはおよそ100um (コマンドラインから指定可能)
res = 100.0
if len(sys.argv) >= 2:
res = float(sys.argv[1])
tmpdir = os.path.join(os.getcwd(), 'work')
outfile = os.path.join(os.getcwd(), 'out.s2p')
unit = 1e-6 # drawing unit in um
# waveguide dimensions
a = 5600 # waveguide width
b = 2800 # waveguide height
# BPF parameter (5段)
wall_t = 200 # 金属壁の厚さ
zofs = 6500 # 入出力に挿入している素管の長さ
d1 = 300 # 金属壁1 長さ
d2 = 2000 # 金属壁2 長さ
d3 = 2425 # 金属壁3 長さ
d4 = 2425 # 金属壁4 長さ
d5 = 2000 # 金属壁5 長さ
d6 = 300 # 金属壁6 長さ
l1 = 3855 # 金属壁1-2 の間隔
l2 = 3880 # 金属壁2-3 の間隔
l3 = 3885 # 金属壁3-4 の間隔
l4 = 3880 # 金属壁4-5 の間隔
l5 = 3855 # 金属壁5-6 の間隔
length = zofs + d1 + l1 + d2 + l2 + d3 + l3 + d4 + l4 + d5 + l5 + d6 + zofs
# frequency range of interest
f_start = 35e9
f_0 = 40e9
f_stop = 45e9
# waveguide TE-mode definition
TE_mode = 'TE10'
# FDTD 初期化, NrTS を大きく、EndCriteria を小さくすると精度はあがるかもしれないが、計算時間が増大する.
FDTD = openEMS(NrTS=1e6, EndCriteria=1e-5)
FDTD.SetGaussExcite(0.5*(f_start+f_stop), 0.5*(f_stop-f_start))
# boundary conditions
FDTD.SetBoundaryCond([0, 0, 0, 0, 3, 3])
# モデルを設定
CSX = ContinuousStructure()
# AddMetal で金属壁構造を定義する
metal = CSX.AddMetal('metal')
start = [(a-wall_t)/2, 0, zofs]
stop = [(a+wall_t)/2, b, zofs+d1]
box = metal.AddBox(start, stop)
start = [(a-wall_t)/2, 0, zofs+d1+l1]
stop = [(a+wall_t)/2, b, zofs+d1+l1+d2]
box = metal.AddBox(start, stop)
start = [(a-wall_t)/2, 0, zofs+d1+l1+d2+l2]
stop = [(a+wall_t)/2, b, zofs+d1+l1+d2+l2+d3]
box = metal.AddBox(start, stop)
start = [(a-wall_t)/2, 0, zofs+d1+l1+d2+l2+d3+l3]
stop = [(a+wall_t)/2, b, zofs+d1+l1+d2+l2+d3+l3+d4]
box = metal.AddBox(start, stop)
start = [(a-wall_t)/2, 0, zofs+d1+l1+d2+l2+d3+l3+d4+l4]
stop = [(a+wall_t)/2, b, zofs+d1+l1+d2+l2+d3+l3+d4+l4+d5]
box = metal.AddBox(start, stop)
start = [(a-wall_t)/2, 0, zofs+d1+l1+d2+l2+d3+l3+d4+l4+d5+l5]
stop = [(a+wall_t)/2, b, zofs+d1+l1+d2+l2+d3+l3+d4+l4+d5+l5+d6]
box = metal.AddBox(start, stop)
FDTD.SetCSX(CSX)
# メッシュを定義
mesh = CSX.GetGrid()
mesh.SetDeltaUnit(unit)
mesh.AddLine('x', np.arange(0, a, res))
mesh.AddLine('y', np.arange(0, b, res))
mesh.AddLine('z', np.arange(0, zofs, res))
mesh.AddLine('z', np.arange(length-zofs, length, res))
## 各区間を区切ってメッシュサイズを決定.
## res で決められた値になるべく近いメッシュサイズで、
## かつ各構造が必ずメッシュにのるようにしている.
zp = zofs
mesh.AddLine('z', np.arange(zp, zp+d1, d1/int(d1/res)))
zp += d1
mesh.AddLine('z', np.arange(zp, zp+l1, l1/int(l1/res)))
zp += l1
mesh.AddLine('z', np.arange(zp, zp+d2, d2/int(d2/res)))
zp += d2
mesh.AddLine('z', np.arange(zp, zp+l2, l2/int(l2/res)))
zp += l2
mesh.AddLine('z', np.arange(zp, zp+d3, d3/int(d3/res)))
zp += d3
mesh.AddLine('z', np.arange(zp, zp+l3, l3/int(l3/res)))
zp += l3
mesh.AddLine('z', np.arange(zp, zp+d4, d4/int(d4/res)))
zp += d4
mesh.AddLine('z', np.arange(zp, zp+l4, l4/int(l4/res)))
zp += l4
mesh.AddLine('z', np.arange(zp, zp+d5, d5/int(d5/res)))
zp += d5
mesh.AddLine('z', np.arange(zp, zp+l5, l5/int(l5/res)))
zp += l5
mesh.AddLine('z', np.arange(zp, zp+d6, d6/int(d6/res)))
# ポート設定
ports = []
start=[0, 0, 1000]
stop =[a, b, 1500]
mesh.AddLine('z', [start[2], stop[2]])
ports.append(FDTD.AddRectWaveGuidePort( 0, start, stop, 'z', a*unit, b*unit, TE_mode, 1))
start=[0, 0, length-1000]
stop =[a, b, length-1500]
mesh.AddLine('z', [start[2], stop[2]])
ports.append(FDTD.AddRectWaveGuidePort( 1, start, stop, 'z', a*unit, b*unit, TE_mode))
# シミュレーション空間指定
Et = CSX.AddDump('Et', file_type=0, sub_sampling=[2,2,2])
start = [0, 0, 0]
stop = [a, b, length]
Et.AddBox(start, stop)
# モデル構造をファイルに書き出し
CSX.Write2XML('bpf.xml')
# 計算実行
FDTD.Run(tmpdir, cleanup=True)
# 計算結果を S-parameter として書き出し
freq = np.linspace(f_start, f_stop, 201)
for port in ports:
port.CalcPort(tmpdir, freq)
s11 = ports[0].uf_ref / ports[0].uf_inc
s21 = ports[1].uf_ref / ports[0].uf_inc
ZL = ports[0].uf_tot / ports[0].if_tot
with open(outfile, 'w') as f:
L = len(freq)
f.write('#HZ S RI R %f\n' % ZL[int(L/2)].real)
for i in range(L):
f.write('%.5f %.5f %.5f %.5f %.5f %.5f %.5f %.5f %.5f\n' % (freq[i], s11[i].real, s11[i].imag, s21[i].real, s21[i].imag, s21[i].real, s21[i].imag, s11[i].real, s11[i].imag))
実行すると bof.xml としてモデルファイルが、out.s2p として計算結果の S-parameter ファイルが出力されます。xml ファイルを AppCSXCAD で開くと以下のような画面でモデルが確認できます。
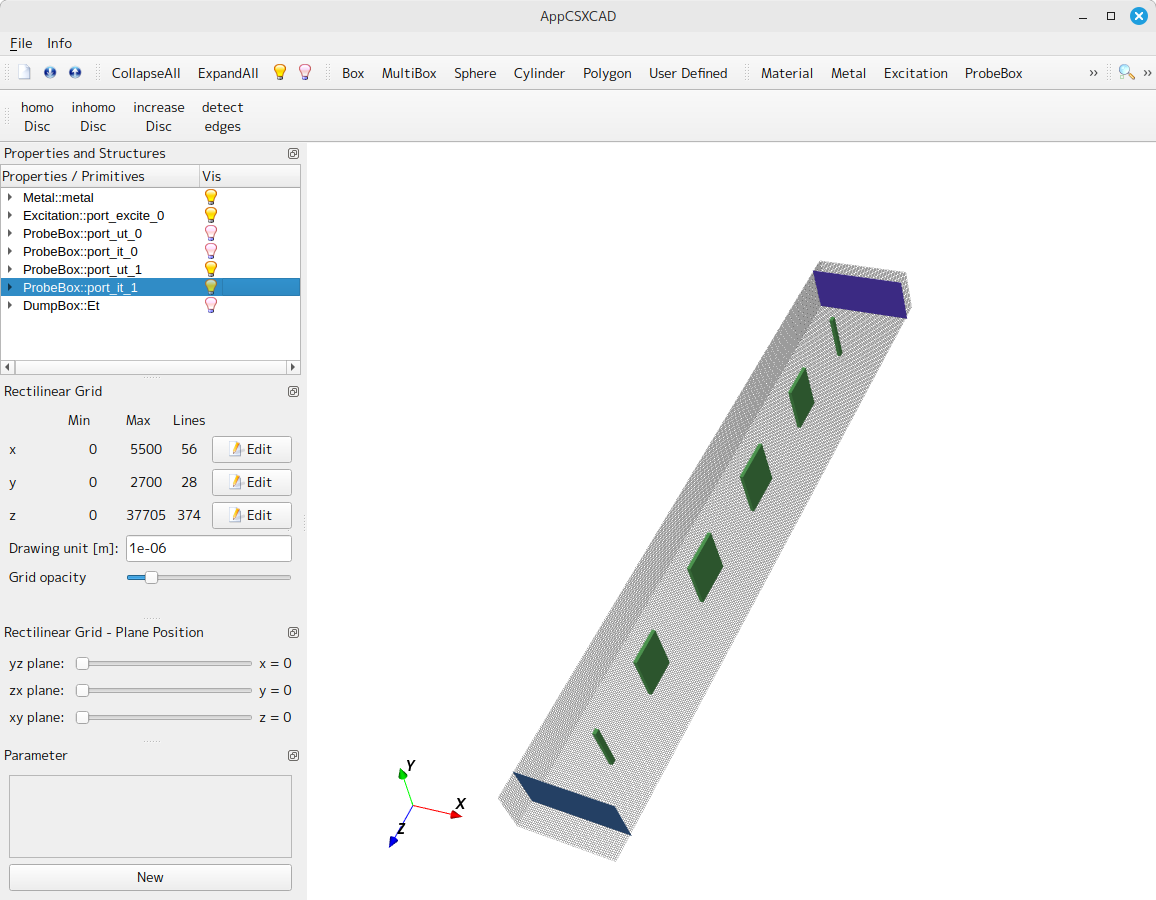
計算結果の確認
メッシュサイズ 100um で計算すると約2分、50um だと約25分ほどで計算が終わりました。それぞれの通過特性の計算結果をプロットしたグラフをこの下に示します。メッシュサイズで結果が変わるというのは予想の範囲内ですが、メッシュ 50um 以下では計算時間はかかりすぎるのでここまでで断念。もっと小さいメッシュも試したかった。まあ、今回はモデル全体をほぼ一様なメッシュサイズにして計算しちゃってるのでムダも多いはずで、特性に効くところは小さく、そうでもないところは大きなメッシュを切るようなことをすれば、計算時間と結果の精度のバランスが丁度よいところを狙えるはずなんですが、そこはノウハウとかあるんでしょう、商用ソフトには敵わないところだと思います。
どちらも BPF っぽい特性がちゃんと出てるのは間違いないんですが、じゃあ正しい結果かというと実際モノ作ったわけではないんで、なんとも言えないところです。参考までに、某商用の有限要素法を用いた電磁界解析ソフトで同じものを計算させてみた結果をプロットしてみたんですが、50um の結果に近い値となってます。こっちの計算は収束条件も緩めでやったのもあり、3分ほどで結果が出るんですが、まあ、少なくとも帯域近辺での結果は経験的に実測とよく合うだろうと思います。なので、メッシュサイズさえ適切なら、openEMS の結果もかなりいいところまでいってると思います。
というわけで、メッシュの設定はちゃんと考えないといけないのと、モデルの入力に難があるので、まあ、単純な構造の、初期検討に関しては、openEMS は十分実用に耐えうるんじゃないかと思います。何にせよ、手元にライセンスを気にしないで使える環境があるのは助かります。

