幅優先探索で迷路の特定のスタート地点からゴール地点までの最短距離を出力するプログラム

■概要

迷路の最短距離を幅優先探索（BFS）で求めるプログラムを実装しました。

基本的なアルゴリズムに対する理解を深め、実際に活用できるようになりたいと思い、今回は幅優先探索の問題を解きました。

以下、解説をしていきます。

※読んでいるだけで理解が難しい場合は、実際にpaiza.IOなどの実行環境に貼り付けて、適宜console.logを入れて処理を追っていただけると内容が理解しやすくなると思います。

https://paiza.io/ja

■問題

AtCoder Beginner Contest 007 atcoder C - 幅優先探索

https://atcoder.jp/contests/abc007/tasks/abc007_3

AtCoderは競技プログラミングの問題を出題するサイトで、定期的にコンテストを開催しています。

今回解いたのはAtCoder Beginner Contestと呼ばれる、初心者向けの問題になります。

入力例

7 8  
2 2  
4 5  
########  
#......#  
#.######  
#..#...#  
#..##..#  
##.....#  
########

まず、問題の要件を洗い出します。

・スタート地点：(2,2)
・ゴール地点：(4,5)
・通行可能：.
・通行不可：#
・スタートからゴールまでの最短マス数を求める

問題文が長いため、

・特に重要そうな条件を書き出す
・タイトルに「幅優先探索」とある→幅優先探索を使いどのように解くか方針を決める

に重点を置いて進めていきます。

■幅優先探索とは？

グラフ探索アルゴリズムの一つで、ノードの隣接するノードを全て探索、さらに隣接するノードを全て探索……と繰り返していき、隣接するノードがなくなるまで探索を繰り返していくアルゴリズムです。

引用元：atcoder

https://atcoder.jp/contests/abc007/tasks/abc007_3

注意点として、訪問済みのノードに対しては再度探索は行わないようにする処理が必要になります。

この処理がないと例えば、

スタート地点→右隣のマス→その左隣のマス（つまりスタート地点）→その右隣のマス……

というように、探索が無限に繰り返されてしまいます。

類似したアルゴリズムに「深さ優先探索」があります。

■幅優先探索と深さ優先探索の違い

	概要	探索するマスを管理する配列	配列の管理方法	メリット	デメリット
幅優先探索	隣接するノードをすべて探索してから、さらに隣接するノードを探索する。別名BFS	キュー	FIFO	全方向に対して探索を繰り返すので、ゴール地点に短時間で到達できる可能性がある	キューのメモリ量が多くなる可能性がある
深さ優先探索	隣接するノードに対し、一方向に進めるだけ進み、行き止まりになったら一つ前のノードに戻って別の方向に探索する。別名DFS	スタック	FILO	一方向に対して探索するので、スタックのメモリ量が少なくて済む可能性がある	ゴール地点に到達するのに時間を要する可能性がある

※メリット、デメリットを可能性がある、としているのは、データの構造により必ずしも当てはまるとは断言できないためです。

例として以下の二分木で幅優先探索と深さ優先探索の違いを確認してみます。

スタート地点はaとします。

番号は探索する順番になります。

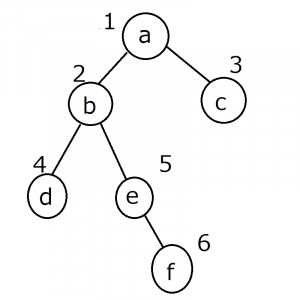
・幅優先探索

aに隣接するb,c→bに隣接するd,e→c(隣接無し)→d(隣接無し)→eに隣接するf→f(隣接無し)

と探索しています。

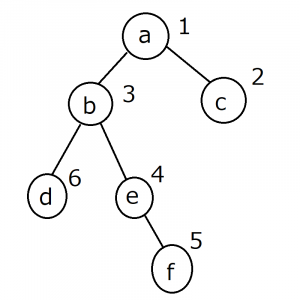
・深さ優先探索

aに隣接するb,c→c(隣接無し)→bに隣接するd,e→eに隣接するf→f(隣接無し)→d(隣接無し)

と探索しています。

■問題を解くにあたり、特に重要そうな条件を書き出します

• 入力の情報

  • y方向の行数、x方向の行数、(yの開始地点,xの開始地点)、(yのゴール地点,xのゴール地点)
    • yとxの順が逆なので注意
    • 全て1で始まる(0開始ではないので注意)

• 地図

  • #は通行不可
  • .は通行可能
  • スタートとゴールは必ず通行可能
  • スタートからゴールへは必ず到達可能
  • 隣接するマス同士の距離は必ず1

• 幅優先探索で、スタートからゴールまで最小移動マス数で移動するよう計算する

  1. スタート地点から、隣接する移動可能なマスを調べ、距離を設定する
  2. 他に隣接するマスに対しても1を行う
  3. さらに隣接するマスに対しても、1,2を行う
  4. ゴール地点に到達するまで繰り返す
     • 探索するマスは作業用キューで管理する
       • 作業用キューの先頭に追加する(shift)
       • 作業用キューの末尾から取り出す(pop)

■コード

process.stdin.resume();  
process.stdin.setEncoding("utf8");

var lines = [];  
var reader = require("readline").createInterface({  
  input: process.stdin,  
  output: process.stdout,  
});

reader.on("line", (line) => {  
  lines.push(line);  
});

reader.on("close", () => {  
  const [maxY, maxX] = lines.shift().split(" ").map(Number);  
  let [startY, startX] = lines.shift().split(" ").map(Number);  
  let [goalY, goalX] = lines.shift().split(" ").map(Number);  
    
  // 入力値は全て1で始まるが、この先配列の添字に使う関係で全て-1する  
  [startY, startX, goalY, goalX] = [  
    startY - 1,  
    startX - 1,  
    goalY - 1,  
    goalX - 1,  
  ];

  // 地図、距離を保管する配列(初期値は-1)を生成する  
  let map = [];  
  let distance = [];  
  for (let i = 1; i <= maxY; i++) {  
    map.push(lines.shift());  
    distance.push(Array(maxX).fill(-1));  
  }

  function bfs(startY, startX, goalY, goalX, map, distance) {  
    distance[startY][startX] = 0;

    // 作業用キューの初期化  
    let queue = [];  
    queue.push([startY, startX]);

    // キューが空になるまでループ  
    while (queue.length != 0) {  
      // キューの先頭から座標を取り出す（幅優先探索の場合）  
    　// 深さ優先探索にしたい場合はshift->popにする  
      let [y, x] = queue.shift();

      // 四方向（上下左右）のマスをチェックする  
      let nextPos = [  
        [0, 1], // 右  
        [1, 0], // 下  
        [-1, 0], // 上  
        [0, -1], // 左  
      ];  
      // 各方向に対して通行可能かつ未訪問であれば処理を行う  
      nextPos.forEach((value) => {  
        let [addy, addx] = [value[0], value[1]];

        // 通行可能で、距離が-1（未訪問）であれば更新し、キューに追加  
        if (  
          map[y + addy][x + addx] == "." &&  
          distance[y + addy][x + addx] == -1  
        ) {  
          // 新しい距離を設定  
          distance[y + addy][x + addx] = distance[y][x] + 1;  
          // 隣接するマスを次に探索するためにキューに追加  
          queue.push([y + addy, x + addx]);  
        }  
      });

      // 追跡用のコメント  
      // console.log("distance", distance);  
      // console.log("queue", queue);  
      // console.log("--------------");  
    }  
      
    // ゴール地点までの距離を返す  
    return distance[goalY][goalX];  
  }

  console.log(bfs(startY, startX, goalY, goalX, map, distance));  
});

■コードの説明

変数・配列の概要

・startY, startX, goalY, goalX：入力値は全て1で始まりますが、この先配列の添字に使う関係で全て-1します。
・map配列：迷路の地図を格納する配列です。
・distance配列：地図のマスに対応する場所の、スタート地点からの距離を格納します。初期値は-1。-1であれば未訪問、つまり探索の対象と判断できます。
・queue配列：作業用キュー。探索の対象となるマスの座標を入れます。pushで追加し、shiftで取り出します（FIFO）。

bfs関数のwhileループ内の処理

・上下左右全方向のマスをチェックします。
・通行可能で、距離が-1(=未訪問)であれば、距離を設定します。
・作業用キューに追加し、隣接するマスのさらに隣接するマスを探索します。
・作業用キューが空になるまで繰り返します。

■実際に動かして追跡してみる

map配列

・迷路のレイアウトを示しています。
・Sがスタート地点、Gがゴール地点を表しています。
わかりやすくするためにこの表記をしており、実際は.が入っています。
・#は壁を、.は通行可能な道を示します。

[  
  [ # , # , # , # , # , # , # , # ],  
  [ # , S , . , . , . , . , . , # ],  
  [ # , . , # , # , # , # , # , # ],  
  [ # , . , . , # , G , . , . , # ],  
  [ # , . , . , # , # , . , . , # ],  
  [ # , # , . , . , . , . , . , # ],  
]

distance配列・queue配列

・初期値

[  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1]  
]

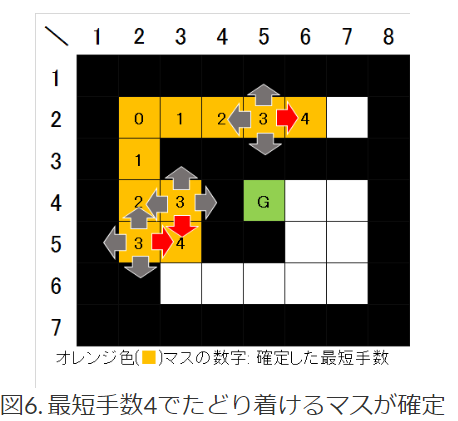
スタート地点から隣接するマスの更新が終わった時の状態
※queueに入っているマスの隣接するマスの座標の距離を次に計算します。

distance [  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1,  0,  1, -1, -1, -1, -1, -1],  
  [ -1,  1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1]  
]  
queue [ [ 1, 2 ], [ 2, 1 ] ]

[ 1, 2 ]に隣接するマスの更新が終わった時

distance [  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1,  0,  1,  2, -1, -1, -1, -1],  
  [ -1,  1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1]  
]  
queue [ [ 2, 1 ], [ 1, 3 ] ]

[ 2, 1 ]に隣接するマスの更新が終わった時

distance [  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1,  0,  1,  2, -1, -1, -1, -1],  
  [ -1,  1, -1, -1, -1, -1, -1, -1],  
  [ -1,  2, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1]  
]  
queue [ [ 1, 3 ], [ 3, 1 ] ]

(以下ゴールに到達するまで繰り返し)

最終的なdistanceの中身

distance [  
  [ -1, -1, -1, -1, -1, -1, -1, -1],  
  [ -1,  0,  1,  2,  3,  4,  5, -1],  
  [ -1,  1, -1, -1, -1, -1, -1, -1],  
  [ -1,  2,  3, -1, 11, 10, 11, -1],  
  [ -1,  3,  4, -1, -1,  9, 10, -1],  
  [ -1, -1,  5,  6,  7,  8,  9, -1],  
  [ -1, -1, -1, -1, -1, -1, -1, -1]  
]  
queue []

ゴール地点の座標でdistance配列にアクセスした値をreturnするので、最終的なスタート地点からゴール地点までの最短経路距離が返ってきます。

■深さ優先探索で求めたい場合

作業用キューから取り出す以下の処理のshiftをpopに変更します。

let [y, x] = queue.shift();   
-> let [y, x] = queue.pop(); 

console.logで仕込んだqueue(作業用キュー)の中身が、shiftとpopでどう変わるかを見てみましょう。

■幅優先探索(shift)の場合

隣接する上下左右のマスを全て調べる→さらに隣接する上下左右のマスを全て調べる、という方法で探索しています。

queue [ [ 1, 2 ], [ 2, 1 ] ]  
queue [ [ 2, 1 ], [ 1, 3 ] ]  
queue [ [ 1, 3 ], [ 3, 1 ] ]  
queue [ [ 3, 1 ], [ 1, 4 ] ]  
queue [ [ 1, 4 ], [ 3, 2 ], [ 4, 1 ] ]  
queue [ [ 3, 2 ], [ 4, 1 ], [ 1, 5 ] ]  
queue [ [ 4, 1 ], [ 1, 5 ], [ 4, 2 ] ]  
queue [ [ 1, 5 ], [ 4, 2 ] ]  
queue [ [ 4, 2 ], [ 1, 6 ] ]  
queue [ [ 1, 6 ], [ 5, 2 ] ]  
queue [ [ 5, 2 ] ]  
queue [ [ 5, 3 ] ]  
queue [ [ 5, 4 ] ]  
queue [ [ 5, 5 ] ]  
queue [ [ 5, 6 ], [ 4, 5 ] ]  
queue [ [ 4, 5 ], [ 4, 6 ] ]  
queue [ [ 4, 6 ], [ 3, 5 ] ]  
queue [ [ 3, 5 ], [ 3, 6 ] ]  
queue [ [ 3, 6 ], [ 3, 4 ] ]  
queue [ [ 3, 4 ] ]  
queue []

■深さ優先探索(pop)の場合

一方向に対し隣接するマスを調べる→さらにそのマスに隣接するマスを調べる→隣接するマスがなくなるまで続け、なくなったら一つ前に戻って別の方向に探索する、という方法で探索しています。

queue [ [ 1, 2 ], [ 2, 1 ] ]
queue [ [ 1, 2 ], [ 3, 1 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 4, 1 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 4, 2 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 5, 2 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 5, 3 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 5, 4 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 5, 5 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 5, 6 ], [ 4, 5 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 5, 6 ], [ 4, 6 ], [ 3, 5 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 5, 6 ], [ 4, 6 ], [ 3, 6 ], [ 3, 4 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 5, 6 ], [ 4, 6 ], [ 3, 6 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 5, 6 ], [ 4, 6 ] ]
queue [ [ 1, 2 ], [ 3, 2 ], [ 5, 6 ] ]
queue [ [ 1, 2 ], [ 3, 2 ] ]
queue [ [ 1, 2 ] ]
queue [ [ 1, 3 ] ]
queue [ [ 1, 4 ] ]
queue [ [ 1, 5 ] ]
queue [ [ 1, 6 ] ]
queue []