この記事は何?
クラスタリングのアルゴリズムで代表的なものとしてk-meansというものがあります.
k-meansは非常に単純なアルゴリズムであるため,残念なクラスタリング結果となってしまうことがあります.
そこで,この記事ではデータ空間を非線形関数によって高次元に写像しクラスタリングを行うkernel k-meansの実装を紹介します.
k-meansの失敗例
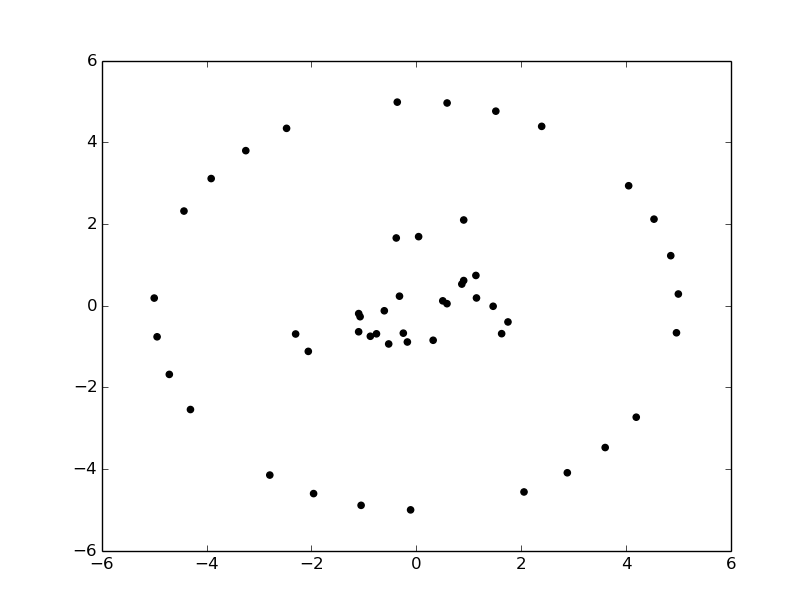
以下のデータをk-meansでクラスタリングを行ってみました.
- クラスタリング前
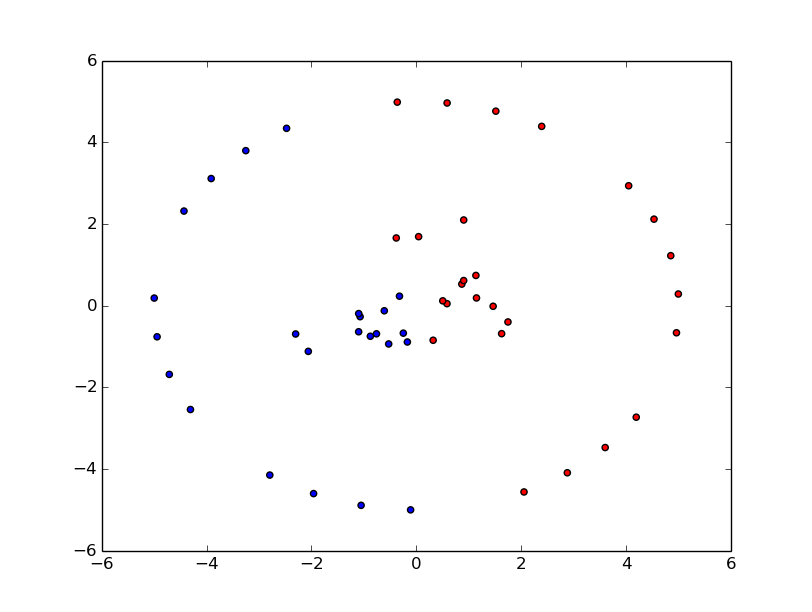
- クラスタリング後
ジーっと見てみると,中央部分と外側部分とでクラスタが2つ存在しているように見えますが,k-meansのクラスタリング結果は直線で区切ったようなものとなっています.
kernel k-means
kernel k-meansではデータ空間を非線形関数によって高次元に写像し,クラスタリングを行います.
つまり,データ点を$x\in X$,非線形関数$\phi$としたときに,$\phi(x)$に対しクラスタリングを行います.
非線形関数$\phi$の選び方は様々なものが考えられますが,$\phi$を選択するよりもカーネル関数$k(x_i,x_j)=\phi(x_i)^T\phi(x_j)$を選択することが多いです(カーネル法).
カーネル関数には以下のようなものがあります.
- 線形カーネル $k(x_i,x_j)=x_i^Tx_j$
- 多項式カーネル $k(x_i,x_j)=(x_i^Tx_j+\gamma)^c$
- ガウスカーネル $k(x_i,x_j)=\exp(-\gamma\cdot||x_i-x_j||^2)$
線形カーネルを選択すると,k-meansと等価となります.
kernel k-meansによるクラスタリング
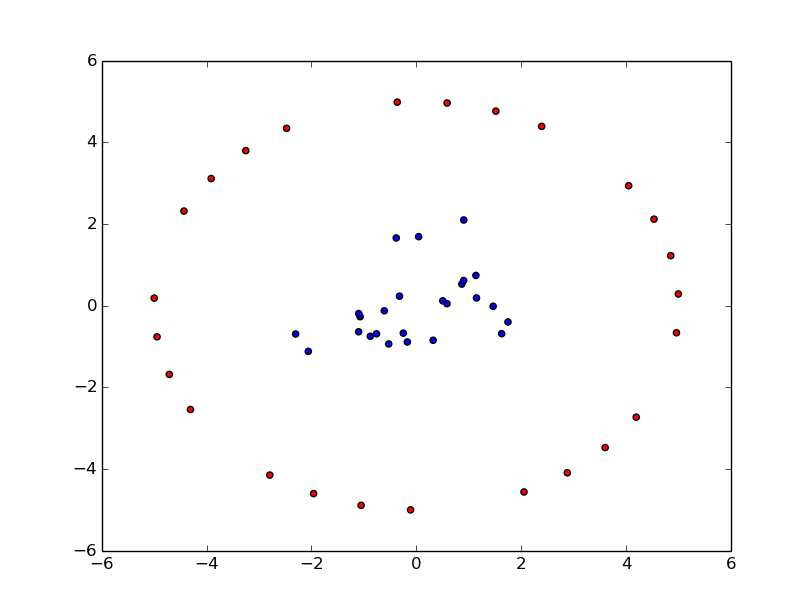
先程のデータに対しkernel k-meansでクラスタリングを行ってみました.
カーネル関数にはガウスカーネルを,$\gamma$の値には0.1を設定してみました.
ソースコードはここにアップロードしました.
中央部分と外側部分とでクラスタリングできていることがわかります.
その他
k-means,kernel k-meansは初期値に大きく依存するアルゴリズムであるため,いつもこのようにクラスタリングできるわけではありません.
kernel k-meansではカーネル関数の選択およびハイパーパラメータの設定を行う必要があるのがメンドウです….
(2015/7/2 微妙に図が異なっていたのを修正)