置換群の計算過程は分かりにくい
置換群の計算過程は分かりにくいのは、関数のようなものなのに記法があまり関数的でないからだと思います。
たとえば、 f(g(x)) と書かれていれば、 y=g(x)を先に計算して、 f(y)を計算するというのは、今までのやり方を踏襲して式変形できますね。
概略
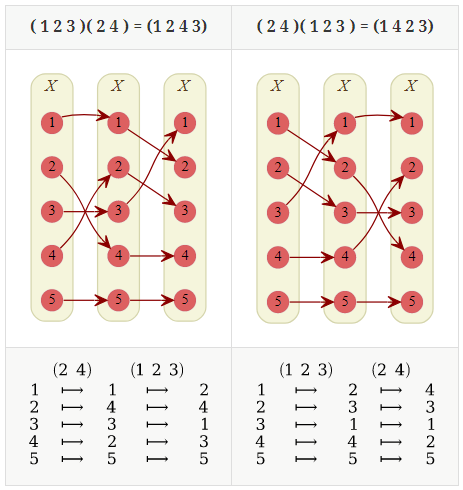
(1 2 3)(2 4) ≠ (2 4)(1 2 3) を例に、関数的な式変形で解いてみる。
σ, τ を次のように定める。
\sigma = (1 \,\,\, 2 \,\,\, 3) = \left(
\begin{array}{ccc}
1 & 2 & 3 & 4 \\
2 & 3 & 1 & 4
\end{array}
\right), \tau = (2 \,\,\, 4) = \left(
\begin{array}{ccc}
1 & 2 & 3 & 4 \\
1 & 4 & 3 & 2
\end{array}
\right)
図解するとこんな感じで非可換です。
関数的に冗長に式変形した例
以下、σ ∘ τ をイメージの部分をあまり省略せずに書いてみた。
\begin{align*}
\sigma \circ \tau
&=
\left(
\begin{array}{cccc}
1 & 2 & 3 & 4 \\
\sigma(\tau(1)) & \sigma(\tau(2)) & \sigma(\tau(3)) & \sigma(\tau(4))
\end{array}
\right) \\
&=
\left(
\begin{array}{cccc}
1 & 2 & 3 & 4 \\
\sigma\left(\left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \end{array}\right)(1)\right) &
\sigma\left(\left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \end{array}\right)(2)\right) &
\sigma\left(\left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \end{array}\right)(3)\right) &
\sigma\left(\left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \end{array}\right)(4)\right)
\end{array}
\right) \\
&=
\left(
\begin{array}{cccc}
1 & 2 & 3 & 4 \\
\sigma(1) & \sigma(4) & \sigma(3) & \sigma(2)
\end{array}
\right) \\
&=
\left(
\begin{array}{cccc}
1 & 2 & 3 & 4 \\
\left(\begin{array}{ccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 1 & 4 \end{array}\right)\left(1\right) &
\left(\begin{array}{ccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 1 & 4 \end{array}\right)\left(4\right) &
\left(\begin{array}{ccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 1 & 4 \end{array}\right)\left(3\right) &
\left(\begin{array}{ccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 1 & 4 \end{array}\right)\left(2\right)
\end{array}
\right) \\
&=
\left(
\begin{array}{ccc}
1 & 2 & 3 & 4 \\
2 & 4 & 1 & 3
\end{array}
\right) \\
&= \{1 \mapsto 2, 2 \mapsto 4, 3 \mapsto 1, 4 \mapsto 3 \} \\
&= (1 \,\,\, 2 \,\,\, 4 \,\,\, 3) \\
\end{align*}
同様に τ ∘ σ はこんな感じ。
\begin{align*}
\tau \circ \sigma
&=
\left(
\begin{array}{ccc}
1 & 2 & 3 & 4 \\
\tau(\sigma(1)) & \tau(\sigma(2)) & \tau(\sigma(3)) & \tau(\sigma(4))
\end{array}
\right) \\
&=
\left(
\begin{array}{ccc}
1 & 2 & 3 & 4 \\
\tau\left(\left(\begin{array}{ccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 1 & 4 \end{array}\right)(1)\right) &
\tau\left(\left(\begin{array}{ccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 1 & 4 \end{array}\right)(2)\right) &
\tau\left(\left(\begin{array}{ccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 1 & 4 \end{array}\right)(3)\right) &
\tau\left(\left(\begin{array}{ccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 1 & 4 \end{array}\right)(4)\right)
\end{array}
\right) \\
&=
\left(
\begin{array}{ccc}
1 & 2 & 3 & 4 \\
\tau(2) & \tau(3) & \tau(1) & \tau(4)
\end{array}
\right) \\
&=
\left(
\begin{array}{ccc}
1 & 2 & 3 & 4 \\
\left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \end{array}\right)(2) &
\left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \end{array}\right)(3) &
\left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \end{array}\right)(1) &
\left(\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \end{array}\right)(4)
\end{array}
\right) \\
&=
\left(
\begin{array}{ccc}
1 & 2 & 3 & 4 \\
4 & 3 & 1 & 2
\end{array}
\right) \\
&= \{1 \mapsto 4, 2 \mapsto 3, 3 \mapsto 1, 4 \mapsto 2 \} \\
&= (1 \,\,\, 4 \,\,\, 2 \,\,\, 3) \\
\end{align*}
射の集合として式変形する例
1→2, 2->3, 3->1 に移す関数を (1 2 3)(x)と見立てて、(1 2 3)(1)=2 とか、(ラムダ式っぽく)扱ってみた例。
ちなみに(1 2 3)の例だと、1, 2, 3 以外は n -> n のように同じ値に移す。
\begin{aligned}
\tau \circ \sigma(X=\{1, 2, 3, 4\})
&= \{X=\{1, 2, 3, 4\} \mapsto \tau(\sigma(X=\{1, 2, 3, 4\}))\} \\
&= \{1 \mapsto \tau(\sigma(1)), 2 \mapsto \tau(\sigma(2)),
3 \mapsto \tau(\sigma(3)), 4 \mapsto \tau(\sigma(4))\} \\
&= \{
1 \mapsto (2 \,\,\, 4)((1 \,\,\, 2 \,\,\, 3)(1)),
2 \mapsto (2 \,\,\, 4)((1 \,\,\, 2 \,\,\, 3)(2)),
3 \mapsto (2 \,\,\, 4)((1 \,\,\, 2 \,\,\, 3)(3)),
4 \mapsto (2 \,\,\, 4)((1 \,\,\, 2 \,\,\, 3)(4))
\} \\
&= \{
1 \mapsto (2 \,\,\, 4)(2),
2 \mapsto (2 \,\,\, 4)(3),
3 \mapsto (2 \,\,\, 4)(1),
4 \mapsto (2 \,\,\, 4)(4)
\} \\
&= \{1 \mapsto 4, 2 \mapsto 3, 3 \mapsto 1, 4 \mapsto 2 \} \\
&= (1 \,\,\, 4 \,\,\, 2 \,\,\, 3)
\end{aligned}
あくまで独自の書き方なので、イメージを掴むだけの話ですが、(1 2 3)を射の集合として射と射の合成と捉えたほうが、暗記的に操作を覚えるよりは抽象的な理解になると思う。
余談
当初、群の入門した段階で置換群に(型的な意味で)何となく気持ち悪さを感じることがあった。
σ, τ 中の数字は x -> y のような射であるが、添え字を扱っているようでもある……とか。
後で群作用というページにたどり着いて、腑に落ちた。群 a, b ∈ G に対して a ∘ b でなく、添え字の集合 X={1, 2, 3, 4} の i ∈ X について、 a ∘ i とやるような感じ。似たような例としては、次のような行列がある。前半の行列の積が群の世界の積。後ろの x,y が群じゃない何か。
\begin{pmatrix}
\cos\theta_1 & -\sin\theta_1 \\
\sin\theta_1 & \cos \theta_1
\end{pmatrix}
\begin{pmatrix}
\cos\theta_2 & -\sin\theta_2\\
\sin\theta_2 & \cos \theta_2
\end{pmatrix}
\begin{pmatrix} x \\ y
\end{pmatrix}