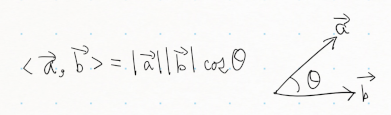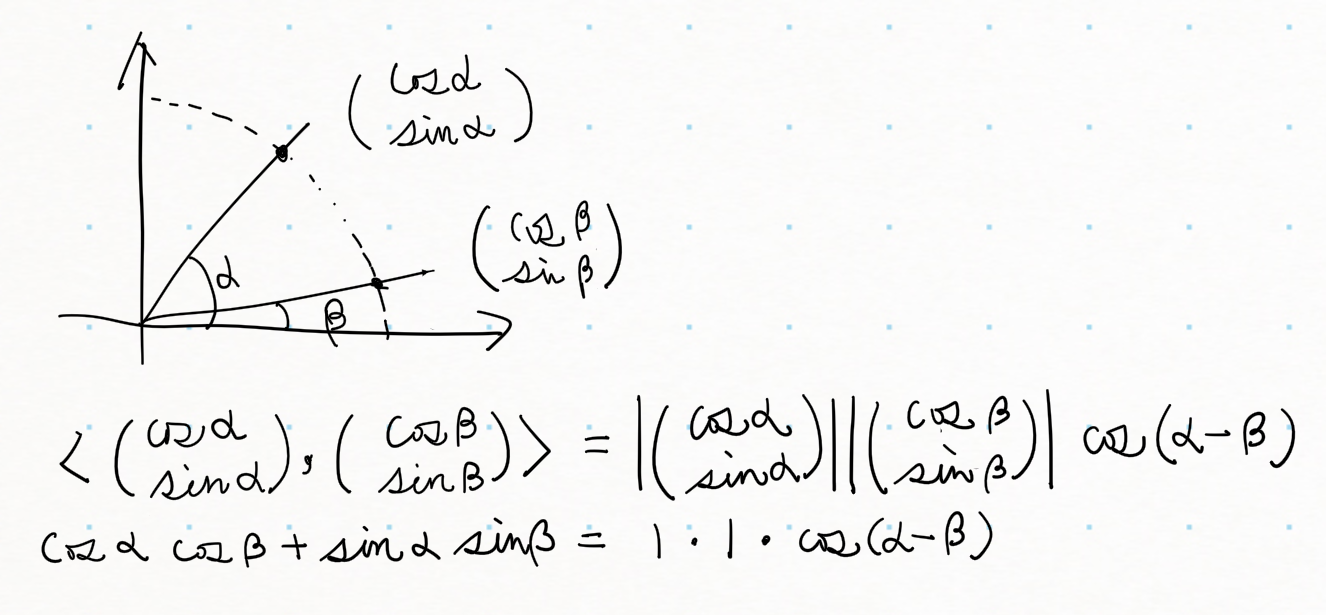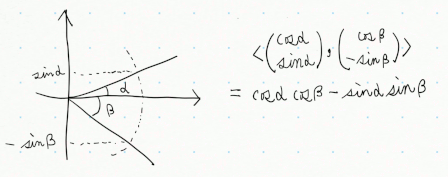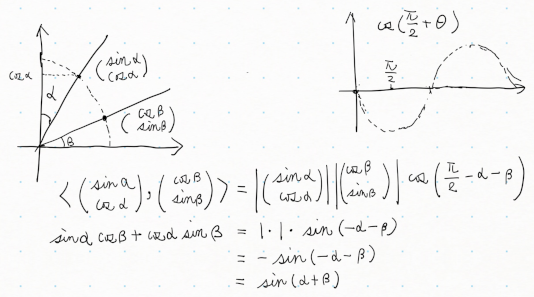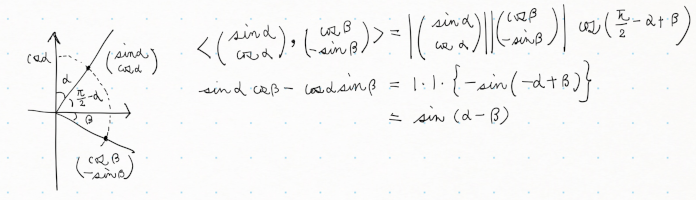内積の公式から、加法定理を思い出す

三角関数の定義の外側の概念である内積の公式を使う時点で、外道ではあるけども、加法定理を思い出しやすいので、時々使う。

次の公式を使う。

\langle\vec{a},\vec{b}\rangle=|\vec{a}||\vec{b}|\cos\theta

$\mathbb{R}^2$で $|\vec{a}|=|\vec{b}|=1$ を満たすとすると、言うまでもなく、こんな風になる。掛けて足すだけ。分かりやすいね。

\begin{align}
\left\langle\vec{a}=\left(\begin{array}{r}x_1 \\ y_1\end{array}\right),\vec{b}=\left(\begin{array}{r}x_2 \\ y_2\end{array}\right) \right\rangle &= |\vec{a}||\vec{b}|\cos\theta \\
x_1 x_2 + y_1 y_2 &= 1 \cdot 1 \cdot \cos \theta 
\end{align}

とはいえ、 加法定理の覚え方。図形でわかる公式の考え方 | アタリマエ！ のサイトにあるようなやり方の方が、前提知識不要な意味で、より良いのであろう。