この記事は古川研究室 Advent Calendar2日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。
はじめに
InfTuckerとはガウス過程に基づいたテンソル分解手法です。(原著論文+DeepLより)
テンソル解析関係の研究を行なっている僕としてはとても実装したい手法なのですが、そもそもガウス過程をわかっていないと手も足も出そうにないので、まずはガウス過程を用いた回帰であるガウス過程回帰を組むことにしました。
ガウス過程回帰の理解、実装においてはガウス過程の青本を参考にしています。アルゴリズムも載っていてすぐに組むことができました。
ガウス過程回帰
ガウス過程とはN個の入力の集合$\mathbf{X}=(x_1,x_2, ... , x_N)$について,多変量ガウス分布に従う同時分布$ p(\mathbf{Y})$を予測し,$\mathbf{X}$に対応する出力 $ \mathbf{Y} = (y_1, y_2, ... , y_N)$を求める確率過程です。
確率過程とは,入力の集合$\mathbf{X}$に対応する確率変数の集合$ \mathbf{Y}$に同時分布$ p(\mathbf{Y})$を与える確率モデルのことを指します。自分はN個の入力に対して、それぞれに対応するN個の出力を確率的に出してくれる装置と解釈しています。
今回実装するガウス過程回帰はガウス過程に基づいた回帰モデルとなっています。ガウス過程回帰は2つの要素で定義されます。
1.入力$\mathbf{X}=(\mathbf{x}_1,...,\mathbf{x}_n)$と出力$\mathbf{Y}=(y_1,...,y_n)$のペアによって構成されている学習データ
2.ある入力$\mathbf{x}$と別の入力$\mathbf{x'}$の類似度(今回はガウスカーネルによって決まる)を与えるカーネル関数$k(\mathbf{x},\mathbf{x'})$
今回はカーネル関数を以下のように定義しています
$$
k(\mathbf{x},\mathbf{x'}) = \exp(-\frac{\beta}{2}||\mathbf{x}-\mathbf{x'}||^2)
$$
$\beta$はカーネルの幅を決めるパラメータです.
学習データが与えられた時のテストデータ$\mathbf{x}^{new}$に対する出力$y^{new}$は以下の確率分布で表されます
$$
p(y^{new}|\mathbf{x}^{new},\mathbf{X},\mathbf{Y})=\mathcal{N}(\mathbf{k}^T_{new}\mathbf{K}^{-1}\mathbf{Y},k_{new,new}-\mathbf{k}^T_{new}\mathbf{K}^{-1}\mathbf{k}_{new})
$$
ここで$\mathbf{k}_{new}$は$\mathbf{X}$と$\mathbf{x}^{new}$のカーネル,$\mathbf{K}$は$\mathbf{X}$と$\mathbf{X}$のカーネル
$k_{new,new}$は$\mathbf{x}^{new}$と$\mathbf{x}^{new}$のカーネルです.
この確率分布を実装し実際に回帰をしてみた結果を以下に乗せています
import numpy as np
import matplotlib.pyplot as plt
class gpr():
def __init__(self, X, beta):
self.X = X
self.DIM = self.X.shape[-1]
self.N = self.X.shape[0]
self.beta = beta
def fit(self):
Xdist = np.sqrt((self.X[:,None,0]-self.X[None,:,0])**2)
Kernel = np.exp((-0.5 * self.beta * Xdist))
self.InvKernel = np.linalg.inv(Kernel)#(NX,NX)
self.yy = self.InvKernel @ self.X[:,1]#NX
def predict_testdata(self, test_data):
self.test_data = test_data
XtrainXtest_dist = np.sqrt((self.X[:,None,0]-self.test_data[None,:,0])**2)
k = np.exp((-0.5 * self.beta * XtrainXtest_dist))#(NX,NY)
Xtest_dist = np.sqrt((self.test_data[:,0]-self.test_data[:,0])**2)
s = np.exp((-0.5 * self.beta * Xtest_dist))#(NY)
self.mu = self.yy@k
self.var = s-k.T@self.InvKernel@k
self.std = np.sqrt(np.diag(self.var))
if __name__ == "__main__":
seed = 8
np.random.seed(seed)
beta_bandwidth = 1
beta = 1.0 / (beta_bandwidth ** 2)
NX = 20
NY = 20
X = np.zeros((NX, 2))
data = np.sort(np.random.rand(NX) * 6-3)
X[:, 0] = data
X[:, 1] = np.sin(data)
test_data = np.zeros((NY, 2))
data = np.sort(np.random.rand(NY) * 6-3)
test_data[:, 0] = data
model =gpr(X,beta)
model.fit()
model.predict_testdata(test_data)
mu = model.mu
var = model.var
std = model.std
# 描画
fig = plt.figure(figsize=(12, 4))
plt.cla()
plt.scatter(X[:, 0], X[:, 1], c="green", marker="+", label="observed data")
plt.plot(test_data[:, 0], mu, color="red", linewidth=1, label="estimated function")
plt.scatter(test_data[:, 0], mu, color="blue",s=10,label="test data")
plt.fill_between(test_data[:, 0], mu+std, mu-std, facecolor='orange', alpha=0.2,label = "std")
plt.legend()
plt.show()
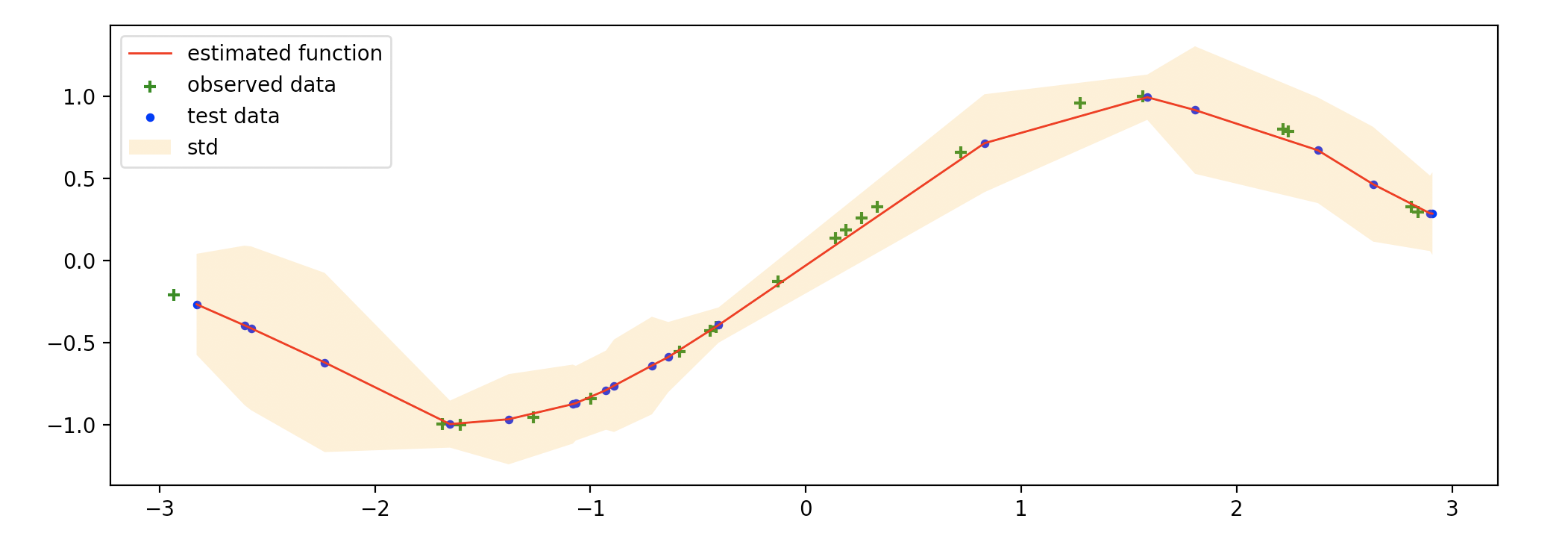
グラフの緑十字は学習するために用いたデータ,青点はテストデータ,赤線はガウス過程回帰により出力されたテストデータに対する関数の平均で、オレンジ色の領域は分散を示しています。
テストデータ、学習データ共にsin関数からサンプリングしているため、赤線もサインカーブのようになっていますが、学習データの少ない部分は分散が大きくなっているなど、確率過程らしい特徴が感じ取れます。このように推定した関数の不確定性まで扱えるのが確率過程の良いところですね
終わりに
InfTuckerを組むための導入として今回はガウス過程回帰を実装しました。
次回はガウス過程回帰をさらに拡張したモデルであるGPLVMを実装して,少しずつInftuckerに近づいていこうと思います.