MLXだけでMNISTを予測してみた（numpy完全排除）

MLXだけ使ってMNISTを予測してみた（numpy完全排除）

はじめに

こんにちは、しゅんです。
今回は Apple が公開した MLX を使って、MNIST（手書き数字）を予測してみました。
前からMLXのことずっと気になっていて今回挑戦することにしました。

---

MLXとは？

MLX は Apple が作った Apple Silicon 専用の機械学習ライブラリです。

公式によるとこんな特徴があります。

特徴	説明
NumPyライク	APIがNumPyにかなり似てる
自動微分	PyTorchっぽいgradで勾配取れる
遅延計算	必要になるまで計算しない
CPU / GPU 両対応	自動的にデバイス最適化
メモリ統一	CPUとGPUの間でメモリコピー不要

→ Apple Silicon (M1, M2, M3, M4系) の性能を最大限に使いやすい構造になっています。
完全に Apple エコシステムのための NumPy x PyTorch x JAX MIX みたいな感じ。

公式ページ: https://ml-explore.github.io/mlx/

---

実験環境

項目	内容
PC	MacBook Pro M4 32GB
ライブラリ	mlx / matplotlib / tqdm / scikit-learn /tensorflow (keras MNISTロード用)
やったこと	MNIST を MLP（2層の全結合）で学習 & 推論

---

インストール方法

MLX などをインストール

pip install mlx
pip install tensorflow  
pip install matplotlib
pip install tqdm
pip install scikit-learn

---

MNISTデータについて（numpyについて少し補足）

MNISTのデータセットは

from tensorflow.keras.datasets import mnist

でロードしていますが、これは keras 側の仕様で numpy.ndarray で返ってきます。

でも安心してください。
numpy を使うのはデータの読み込みと前処理だけで、
この後の 学習・推論・計算処理はすべて MLX のみ で動いています。

図にするとこんな感じ↓

keras.mnist.load_data() 
→ numpy形式のデータが返ってくる
→ reshapeと正規化だけ numpyで実行
→ mx.array() に変換
→ 以降の学習・推論は MLX のみ

つまり numpy は

"kerasから受け取った箱をmlxに渡すだけの役割"

計算は一切していません。numpy 完全排除です。

---

最終的なコード

import mlx.core as mx                 # MLX ライブラリ（高速な自動微分、遅延評価などを提供）
import matplotlib.pyplot as plt        # プロット用ライブラリ
from tensorflow.keras.datasets import mnist  # MNIST データセットのロード用
from tqdm import tqdm                  # 進捗表示用ライブラリ
from sklearn.metrics import confusion_matrix  # 混同行列の計算（評価用）
import random                          # Python 標準の乱数モジュール（データシャッフル用）

# ------------------------------------------------------------------
# 1. 乱数シードの設定
# MLX の内部乱数シードを設定することで、MLX 内部で発生する乱数に基づく計算の再現性を高める
mx.random.seed(0)
# また、Python 標準の random モジュールも固定し、データシャッフル時の順番を固定する
random.seed(0)

# ------------------------------------------------------------------
# 2. ログ用リストの初期化
# 各エポックでの平均損失（loss）やトレーニング正解率（accuracy）を記録するためのリスト
loss_history = []
train_acc_history = []

# ------------------------------------------------------------------
# 3. データの読み込みと前処理
# mnist.load_data() は numpy 配列を返すため、ここでは初期の reshape や正規化のみ numpy を使用します。
# ※その後の学習・評価は MLX の array 関数を用いて MLX 配列に変換して行います。
(x_train_raw, y_train_raw), (x_test_raw, y_test_raw) = mnist.load_data()

# 入力画像はもともと (サンプル数, 28, 28) の形状なので、これを (サンプル数, 28*28) = (サンプル数, 784) に平坦化します。
# さらに、ピクセル値を 0～255 から 0～1 の実数に正規化します。
x_train_raw = x_train_raw.reshape(-1, 28 * 28).astype('float32') / 255.0
x_test_raw  = x_test_raw.reshape(-1, 28 * 28).astype('float32') / 255.0

# MLX の array 関数を使って、numpy 配列から MLX 配列に変換します。
x_train = mx.array(x_train_raw)
y_train = mx.array(y_train_raw)  # ラベルは整数のまま
x_test  = mx.array(x_test_raw)
y_test  = mx.array(y_test_raw)

# ------------------------------------------------------------------
# 4. モデルの定義 (MLP)
def model(params, x):
    """
    2層全結合ニューラルネットワークの定義
      - 入力: flatten された 784 次元のベクトル（28×28 の画像）
      - 隠れ層: 線形変換 (x @ w1 + b1) を計算し、ReLU 活性化 (mx.maximum(..., 0)) を適用
      - 出力層: 隠れ層から各クラスのロジット（生のスコア）を計算
    """
    # 第1層の線形変換および ReLU 活性化
    hidden = mx.maximum(x @ params['w1'] + params['b1'], 0)
    # 第2層で隠れ層から出力層への線形変換を実施し、ロジットを返す
    return hidden @ params['w2'] + params['b2']

# ------------------------------------------------------------------
# 5. 損失関数 (Loss) の定義
def loss_fn(params, x, y):
    """
    クロスエントロピー損失を計算する関数
      1. モデル出力（ロジット）を計算
      2. 数値安定化のため、各サンプルごとに最大値を引く（オーバーフロー防止）
      3. softmax を計算し、各クラスの確率に変換
      4. log をとり、正解ラベルに対応する対数確率の負の平均を損失として返す
    """
    logits = model(params, x)
    # 各サンプルの最大値を引いて、数値安定化
    logits = logits - mx.max(logits, axis=1, keepdims=True)
    exp_logits = mx.exp(logits)
    softmax = exp_logits / mx.sum(exp_logits, axis=1, keepdims=True)
    log_probs = mx.log(softmax)
    # 各サンプルごとに、正解ラベルに対応する log probability を抽出
    correct_log_probs = log_probs[mx.arange(x.shape[0]), y]
    return -mx.mean(correct_log_probs)

# ------------------------------------------------------------------
# 6. 正解率 (Accuracy) の定義
def accuracy_fn(params, x, y):
    """
    モデルの正解率を計算する関数
      モデル出力のロジットから argmax を計算し、予測クラスと正解ラベルの一致率を算出
    """
    logits = model(params, x)
    preds = mx.argmax(logits, axis=1)
    return mx.mean(preds == y)

# ------------------------------------------------------------------
# 7. パラメータ初期化 (MLX の乱数関数とゼロ初期化)
# ここでは、numpy を使わずに MLX の乱数関数 mx.random.normal と mx.zeros を用いて初期化します。
# ----- パラメータ初期化 (MLX の乱数関数を利用) -----
w1 = mx.random.normal((28 * 28, 128), mx.float32, 0.0, 1.0) * 0.01
w2 = mx.random.normal((128, 10), mx.float32, 0.0, 1.0) * 0.01
b1 = mx.zeros((128,), mx.float32)
b2 = mx.zeros((10,), mx.float32)

params = {
    'w1': w1,
    'b1': b1,
    'w2': w2,
    'b2': b2
}


# ------------------------------------------------------------------
# 8. トレーニング設定
lr = 0.1             # 学習率（SGD のステップサイズ）
batch_size = 64      # ミニバッチのサイズ
epochs = 5           # エポック数（訓練データ全体の反復回数）
num_train = x_train.shape[0]  # 訓練データのサンプル数

# ------------------------------------------------------------------
# 9. トレーニングループ
for epoch in range(epochs):
    # 1エポックごとに訓練データの全インデックスリストを作成し、Python 標準の random.shuffle でシャッフル
    indices = list(range(num_train))
    random.shuffle(indices)
    epoch_loss = 0.0
    num_batches = 0
    
    # tqdm を用いて、ミニバッチごとの処理進捗を表示
    for start in tqdm(range(0, num_train, batch_size), desc=f"Epoch {epoch+1}"):
        end = start + batch_size
        idx = indices[start:end]
        # シャッフルされたインデックスに基づいてミニバッチデータを MLX 配列に変換
        xb = mx.array(x_train[idx])
        yb = mx.array(y_train[idx])
        
        # 損失関数を計算し、MLX の自動微分 (mx.grad) で勾配を算出
        loss = loss_fn(params, xb, yb)
        grads = mx.grad(loss_fn)(params, xb, yb)
        
        # 確率的勾配降下法 (SGD) により各パラメータを更新
        params = {k: params[k] - lr * grads[k] for k in params}
        
        # MLX のスカラー値は float() で取得し、エポック内で累積
        epoch_loss += float(loss)
        num_batches += 1
    
    avg_loss = epoch_loss / num_batches
    # エポック終了時に、訓練データ全体での正解率を計算（MLX 配列に再変換して評価）
    acc = float(accuracy_fn(params, mx.array(x_train), mx.array(y_train)))
    print(f'Epoch {epoch+1} | Avg Loss: {avg_loss:.4f} | Train Acc: {acc:.4f}')
    
    # 各エポックの結果をログ用リストに保存
    loss_history.append(avg_loss)
    train_acc_history.append(acc)

# ------------------------------------------------------------------
# 10. テスト評価
# テストデータに対してモデルの正解率を評価
test_acc = float(accuracy_fn(params, x_test, y_test))
print(f'Test Accuracy: {test_acc:.4f}')

# ------------------------------------------------------------------
# 11. 予測と混同行列の計算
# モデルを用いてテストデータのロジットを計算し、argmax により予測クラスを取得
logits = model(params, x_test)
preds = mx.argmax(logits, axis=1)
# MLX の配列を Python のリストに変換（tolist() を利用）
preds_list = preds.tolist()
y_test_list = y_test.tolist()

# sklearn を用いて混同行列を計算
cm = confusion_matrix(y_test_list, preds_list)

# 混同行列のプロット
plt.figure(figsize=(8, 6))
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.title('Confusion Matrix')
plt.colorbar()
tick_marks = list(range(10))
plt.xticks(tick_marks, tick_marks)
plt.yticks(tick_marks, tick_marks)
thresh = cm.max() / 2.0
for i in range(len(cm)):
    for j in range(len(cm[i])):
        plt.text(j, i, format(cm[i][j], 'd'),
                 horizontalalignment="center",
                 color="white" if cm[i][j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
plt.show()

# ------------------------------------------------------------------
# 12. 損失 (Loss) と正解率 (Accuracy) の推移プロット
plt.figure()
plt.plot(loss_history, marker='o', label='Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
plt.title('Training Loss')
plt.show()

plt.figure()
plt.plot(train_acc_history, marker='o', label='Train Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
plt.title('Training Accuracy')
plt.show()

# ------------------------------------------------------------------
# 13. 誤分類例と正解例の可視化
# 予測結果と正解ラベルのリストから、誤分類と正解のインデックスを取得する
wrong_idx = [i for i, (p, t) in enumerate(zip(preds_list, y_test_list)) if p != t]
print(f'間違えた数: {len(wrong_idx)}')

plt.figure(figsize=(10, 10))
# 誤分類例の上位 16 件をプロット
for i, idx in enumerate(wrong_idx[:16]):
    plt.subplot(4, 4, i + 1)
    # 描画用には最初に変換した x_test_raw (numpy 配列) を利用
    plt.imshow(x_test_raw[idx].reshape(28, 28), cmap='gray')
    plt.title(f'Pred: {preds_list[idx]}, True: {y_test_list[idx]}')
    plt.axis('off')
plt.tight_layout()
plt.show()

correct_idx = [i for i, (p, t) in enumerate(zip(preds_list, y_test_list)) if p == t]
print(f'正解数: {len(correct_idx)}')

plt.figure(figsize=(10, 10))
# 正解例の上位 16 件をプロット
for i, idx in enumerate(correct_idx[:16]):
    plt.subplot(4, 4, i + 1)
    plt.imshow(x_test_raw[idx].reshape(28, 28), cmap='gray')
    plt.title(f'Pred: {preds_list[idx]}, True: {y_test_list[idx]}')
    plt.axis('off')
plt.tight_layout()
plt.show()

結果

学習中のログ（5エポック）

(.venv) syun@syunnoMacBook-Pro mlx_learning % python MLX_MNIST_ver2.py
Epoch 1: 100%|█████████████████████████████████████████████████████| 938/938 [00:00<00:00, 1698.68it/s]
Epoch 1 | Avg Loss: 0.5432 | Train Acc: 0.9192
Epoch 2: 100%|█████████████████████████████████████████████████████| 938/938 [00:00<00:00, 1758.31it/s]
Epoch 2 | Avg Loss: 0.2409 | Train Acc: 0.9379
Epoch 3: 100%|█████████████████████████████████████████████████████| 938/938 [00:00<00:00, 1859.54it/s]
Epoch 3 | Avg Loss: 0.1809 | Train Acc: 0.9560
Epoch 4: 100%|█████████████████████████████████████████████████████| 938/938 [00:00<00:00, 1838.07it/s]
Epoch 4 | Avg Loss: 0.1455 | Train Acc: 0.9619
Epoch 5: 100%|█████████████████████████████████████████████████████| 938/938 [00:00<00:00, 1821.10it/s]
Epoch 5 | Avg Loss: 0.1222 | Train Acc: 0.9701
Test Accuracy: 0.9675
間違えた数: 325
正解数: 9675

Confusion Matrix（混同行列)

Lossの推移

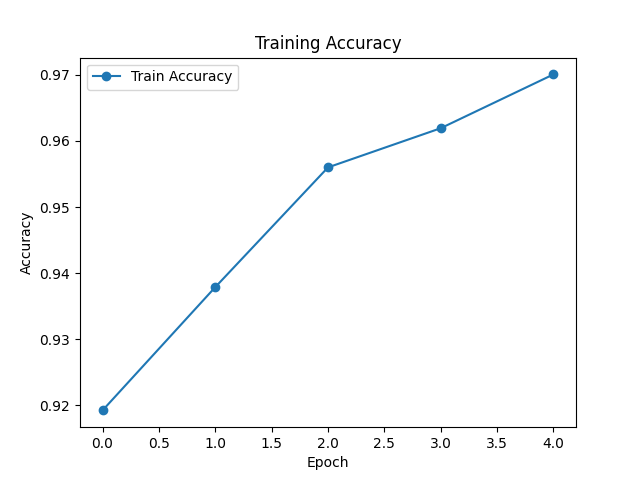
Accuracyの推移

誤分類の例

正解の例

---

感想

• MLX 想像以上に使いやすい
• numpyと同じ感覚で書ける
• 勾配計算と更新が超シンプル
• メモリの扱いとか何も気にしなくていいの最高
• Apple Siliconで学習めちゃくちゃ速い（少なくとも今回は早かった謎）
• 遅延評価の恩恵も正直よくわからんけどとりあえず回すことはできたので、困ってない（まだ勉強中）
• 今回は MLP（2層の全結合）で MNISTだったけど CNN とか Transformer 系も MLXだけでいけそう
• ですがCNNを試して作ろうとしたがうまくいかなかった。

---

最後に

Macユーザーで機械学習やりたい人には間違いなくやってみる価値もあるしおすすめ。
numpyっぽく書けて、PyTorchっぽい使い方ができて、しかも Apple Silicon 最適化。

次は:

• CNNバージョン（すでに試してるが上手くいってない）
• 自作データセット
• 学習曲線の比較
• PyTorch vs MLX 比較記事

これらもやっていきたいともいます。

今回も最後まで読んでくれてありがとうございました！
質問・アドバイス・コメント大歓迎です！