カウントゲームを題材にGrundy数の計算を練習

競技プログラミングでたまに二人ゲームの勝敗判定を問われることがあります。特定の性質を持つゲームなら「Grundy数」によって評価できるということを知り、詳細を以下のサイトで学習しました。

そしてついにGrundy数が向いている問題に出くわしたところ、部分ゲームの評価を考えるのに1時間以上かかり、ギリギリ時間切れとなってしまいました。

---

Grundy数の強力なところは複数に分割できるゲームの全体を排他的論理和（XOR）で評価できることですが、そのためにはまず個別のゲームを評価できる必要があります。Nimだと個別のゲーム（1山）の評価は簡素で、もう少し違う例でも練習しておかないと身につかないと感じました。

2山のNimより単純なゲームがないか考えたところ、カウントゲーム（「21ゲーム」など）が身近で良さそうに感じたので、実際にやってみます。特に、Grundy数の計算時に迷子にならないよう、局面の遷移をグラフで表しながら考えてみます。
※ 冒頭の参考サイトでは同様のゲームを「個数制限Nim」の部分ゲームとして扱っています。

手順

1. ゲームの局面を列挙する
   • 手詰まり（→手番の人の負け）の局面を必ず入れる
   • 序盤までの全てを考える必要は無いが、終盤に近いものは網羅的に
     • 間を「…」で省略すると後々難しくなるので、最初のうちは具体的なゲーム設定で
   • 局面を端的に表す値を割り振っておく（整数だったり配列だったり）
2. 局面の遷移を全て列挙する
   • グラフで表せば、局面は頂点、遷移は有向辺となる
3. Grundy数を各局面について求めてみる
   1. 手詰まりの局面に 0 を割り当てる
   2. 遷移先の局面のGrundy数が全て求まっている局面について、新たにGrundy数を求める…という作業を繰り返す
4. 局面からGrundy数を求める数式を見つける
   • 単純なゲームならすぐ法則性が見えるはず
   • 複雑だったり証明が必要なら、数学的帰納法などで頑張る
5. 最初の局面のGrundy数を求めて、勝敗判定する

カウントゲームのルールの設定

いくつかパラメーターがあり変種を作れるので、検索して出てきやすかった「21ゲーム」に沿います。

• 二人が交互に、 1 から順に数をいくつか言っていく
• 一度に言える数は 1 ～ 3 個
• 21 を言った方が 負け

実際に手順を実行

ゲームの局面を列挙する

局面の表し方を「最後に言った数」とするか「次に言う数」とするかで少し考え方が変わりそうですが、同じ局面に別のIDが付くだけなので気にしなくていいです。今回は「次に言う数」で考えてみます。すると 1 〜 21 の21個の局面が出てきます。特に局面 21 は、その時点で手番の人が負けとなります。

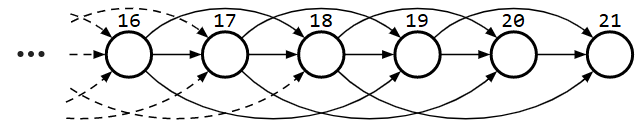
グラフで表すために、終盤に近い6局面だけ紙に描いてみます。（想像するのに足りなければ後から増やせばいいです）

局面の遷移を全て列挙する

次に言う数が 21 なら、その時点で手番の人が負けのため、他の局面には遷移しません。

他の局面も考えていきます。どこから考えてもいいですが、ひとまず最後に近い局面から順にやってみます。

• 20 からは数を1個言って 21 に遷移できる（それしか手が無い）
• 19 からは数を1個言って 20 か、2個言って 21 に遷移できる
• 18 からは 19, 20, 21 に遷移できる
• 17 からは 18, 19, 20 に遷移できる（直接 21 には遷移できない）
• …

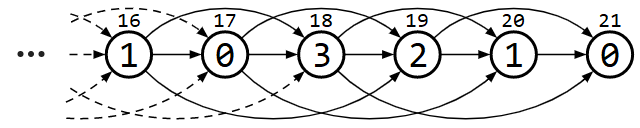
これをグラフに描き込めば以下のようになります。

Grundy数を各局面について求めてみる

mex という関数（引数の集合に無い最小の非負整数を返す）を使って、各局面のGrundy数を順次求めていきます。

擬似コード（再帰）

# 局面 k （遷移先の局面のリスト dst[k] ）のGrundy数を求める
def grundy(k):
    return mex({grundy(i) for i in dst[k]})

遷移先の局面のGrundy数が全て求まっていないといけないため、手計算する場合は最後の局面から順に求める必要があります。

局面 21 については、手詰まりなのでGrundy数は 0 です。（遷移先が無いので空集合を用いて mex({}) = 0 、と計算もできます）

その他は地道に求めていきます。遷移先を間違えると計算が狂うので、グラフも見ながら慎重に。

• 局面 20 は、遷移できる局面が 21 （Grundy数 0 ）なので、 mex({0}) = 1
• 局面 19 は、遷移できる局面が 21 と 20 （Grundy数 0, 1 ）なので、 mex({0, 1}) = 2
• 局面 18 は、遷移できる局面が 21 〜 19 （Grundy数 0 〜 2 ）なので、 mex({0, 1, 2}) = 3
• 局面 17 は、遷移できる局面が 20 〜 18 （Grundy数 1 〜 3 ）なので、 mex({1, 2, 3}) = 0
• 局面 16 は、遷移できる局面が 19 〜 17 （Grundy数 2, 3, 0 ）なので、 mex({0, 2, 3}) = 1
• …

局面からGrundy数を求める数式を見つける

最後の局面から順に見てみると、Grundy数は 0, 1, 2, 3 が循環しているようです。

局面を表している「次に言う数」の値からこれらのGrundy数を求める方法を考えると、局面を k として (21 - k) mod 4 とすればうまく求められます。

最初の局面のGrundy数を求めて、勝敗判定する

最初の局面は「次に言う数が 1 」です。（手番はもちろん先手です）

前節の式に k = 1 を当てはめると、 (21 - 1) mod 4 = 0 なのでGrundy数は 0 となります。 0 は手番の人が負けるので、このゲームは互いに最善を尽くせば先手の負け（後手必勝）です。

もっと単純な勝敗判定との比較

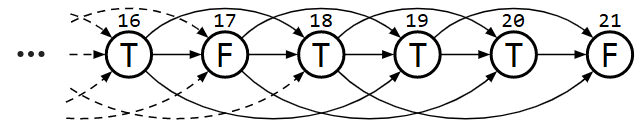
ゲームを分割せず評価するなら、各局面についてGrundy数でなく勝敗の2値（booleanなど）を直接求めるほうが楽です。Grundy数の計算方法を知っているのなら、例えば Grundy数 != 0 という形で変換すれば自然と導けます。

• 手番の人が勝てる局面なら True 、負ける局面なら False
• 局面を評価するときは mex の代わりに「 False な局面への遷移が存在するか」
  • つまり、負ける局面を相手に押し付ける手があるなら勝てる