12月12日7時追記
コメントでご指摘いただいたミスを訂正いたしました。
(監視カメラの向きの最小が0°未満になる場合、最大が360°以上になる場合を考慮していませんでした)
検証が不十分のまま投稿してしまい、誠に申し訳ございませんでした。
1.前編のあらすじ
真正面にいる人をスルーする、常識に囚われない監視カメラを作成しました。
前編の最後に登場したプログラム(クリックすると開きます)
import java.util.Scanner;
class CameraTest {
public static void main(String[] args) {
// 入力
Scanner sc = new Scanner(System.in);
// プレイヤー
double px = sc.nextDouble(); // プレイヤーのx座標
double py = sc.nextDouble(); // プレイヤーのy座標
Player player = new Player(px, py);
// 監視カメラ
int N = sc.nextInt(); // 監視カメラの台数
for (int n = 0; n < N; n ++) {
// 監視カメラごとの入力・処理
double x = sc.nextDouble(); // 監視カメラのx座標
double y = sc.nextDouble(); // 監視カメラのy座標
double d = sc.nextDouble(); // 監視カメラが視認できる距離
double e = sc.nextDouble(); // 監視カメラの向き(direction)を表す角度
double f = sc.nextDouble(); // 監視カメラの視野角
Camera camera = new Camera(x, y, d, e, f);
if (camera.findPlayer(player)) {
System.out.println("視認できた");
} else {
System.out.println("視認できなかった");
}
}
sc.close();
}
}
class Player {
private double x; // プレイヤーのx座標
private double y; // プレイヤーのy座標
public Player(double x, double y) {
this.x = x;
this.y = y;
}
public double getX() {
return this.x;
}
public double getY() {
return this.y;
}
}
class Camera {
private double x; // 監視カメラのx座標
private double y; // 監視カメラのy座標
private double distance; // 監視カメラが視認できる距離
private double dirAngle; // 監視カメラの向き(direction)を表す角度
private double viewAngle; // 監視カメラの視野角
public Camera(double x, double y, double d, double e, double f) {
this.x = x;
this.y = y;
this.distance = d;
this.dirAngle = e;
this.viewAngle = f;
}
public boolean findPlayer(Player player) {
double px = player.getX();
double py = player.getY();
// 距離による判定
double d = Math.sqrt(Math.pow(this.x - px, 2) + Math.pow(this.y - py, 2));
if (d > this.distance) {
return false;
}
// 角度による判定
double a = Math.toDegrees(Math.atan2(py - this.y, px - this.x));
double aMin = this.dirAngle - this.viewAngle/2;
double aMax = this.dirAngle + this.viewAngle/2;
if (a < aMin || aMax < a) {
return false;
}
return true;
}
}
2.デバッグ
問題点 その1
今回のプログラミングにおける__最大の悪__は、よく調べもせず曖昧なままライブラリを使っていたことです。誤解のないように申し上げますが、ライブラリを使うことが悪いのではありません(むしろ、自分で変ちくりんなメソッドを作ってしまうよりも、ライブラリを使った方がはるかに効率的です)。__よく調べずに使うこと__が悪なのです。具体的にどの部分が悪だったのかを見ていきます。
結論を言ってしまうと、CameraクラスのfindPlayerメソッド中にある角度による判定で、ライブラリのatan2メソッドを使っている部分です。このメソッドの返り値に注目してみます。
atan2メソッドはどんなメソッド?
オラクルのホームページより ※読みやすいよう、少しだけ体裁を変えています。
https://docs.oracle.com/javase/jp/1.4/api/java/lang/Math.html#atan2(double,%20double)
public static double atan2(double y, double x)(クリックすると開きます)
直交座標 (x, y) を極座標 (r, theta) に変換します。このメソッドは、y/x の逆正接 (アークタンジェント) を __-pi ~ pi の範囲__で計算して、位相 theta (シータ) を求めます。特例として、
- どちらかの引数が NaN の場合、結果は NaN になります。
- 1 番目の引数が正のゼロで 2 番目の引数が正、または 1 番目の引数が正の有限で 2 番目の引数が正の無限大の場合、結果は正のゼロになります。
- 1 番目の引数が負のゼロで 2 番目の引数が正、または 1 番目の引数が負の有限で 2 番目の引数が正の無限大の場合、結果は負のゼロになります。
- 1 番目の引数が正のゼロで 2 番目の引数が負、または 1 番目の引数が正の有限で 2 番目の引数が負の無限大の場合、結果は pi にもっとも近似の double 値になります。
- 1 番目の引数が負のゼロで 2 番目の引数が負、または 1 番目の引数が負の有限で 2 番目の引数が負の無限大の場合、結果は -pi にもっとも近似の double 値になります。
- 1 番目の引数が正で 2 番目の引数が正または負のゼロ、または 1 番目の引数が正の無限大で 2 番目の引数が有限の場合、結果は pi/2 にもっとも近似の double 値になります。
- 1 番目の引数が負で 2 番目の引数が正または負のゼロ、または 1 番目の引数が負の無限大で 2 番目の引数が有限の場合、結果は -pi/2 にもっとも近似の double 値になります。
- どちらの引数も正の無限大の場合、結果は pi/4 にもっとも近似の double 値になります。
- 1 番目の引数が正の無限大で 2 番目の引数が負の無限大の場合、結果は 3*pi/4 にもっとも近似の double 値になります。
- 1 番目の引数が負の無限大で 2 番目の引数が正の無限大の場合、結果は -pi/4 にもっとも近似の double 値になります。
- どちらの引数も負の無限大の場合、結果は -3*pi/4 にもっとも近似の double 値になります。
結果は正しく丸めた結果の 2 ulp 以内でなければなりません。結果は半単調なものに限ります。
パラメータ:
y - 縦座標
x - 横座標
戻り値:
直交座標 (デカルト座標) 上の点 (x, y) に対応する極座標上の点 (r, theta) の theta (シータ) 成分要は、普通にtanの逆関数(ライブラリのatanメソッド)を使うだけだと、引数の$x$成分、$y$成分をもつベクトルの__方向__1しか分からないため、ベクトルの__向き__1を調べるために各成分の符号も見る必要があるのですね。そんな素敵な処理を実装したものがatan2メソッドなのです。
で、最も重要なのが赤の太字で示した返り値の部分で、-pi ~ pi の範囲というのは角度を弧度法2で表したもので、これを度数法2に変換する(ライブラリのtoDegreesメソッド)と、-180° ~ 180°となります。もう少し厳密に調べますと、$x$成分が-1、$y$成分が0のときに、atan2メソッドから返された値をさらにtoDegreesメソッドで度数法に直すと180.0となりましたので、どうやら左向きのベクトルに対しては-180°ではなく180°となるようです。つまり、正しくは__-180°より大きく、かつ180°以下__の値を返すことになります。
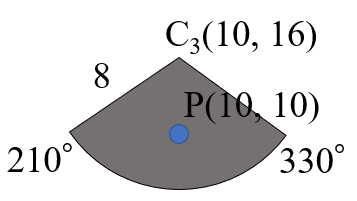
ようやく核心に辿り着きました。私は最初に、監視カメラの視野角を__0°以上360°未満__と決めました。しかし、プログラムで求めたプレイヤーの向きは__-180°より大きく、かつ180°以下__だった訳です。実際に、前回失敗した例を使って、プレイヤーの向きを表す角度も表示しながら確かめてみましょう。
10 16 8 270 120 a = -90.0 aMin = 210.0, aMax = 330.0 視認できなかったなるほど。監視カメラは210°以上330°以下の範囲をカバーしているのに、プレイヤーは範囲外の角度として計算されてしまったため、スルーされてしまった訳ですね。それでは、プレイヤーの向きを表す角度が監視カメラの視野角の範囲外、すなわち__-180°より大きく、かつ0°未満__のときに行うべき処理を考えていきましょう。
そもそも、負の角度なんて日常ではほとんど使わないため、面食らってしまう方もいらっしゃると思いますが、原理が分かってしまえばそれ程難しくはありません。簡単に言うと、反時計回りに回転したときは正の角度で、時計回りに回転したときは負の角度で表しているだけです。たとえば、時計回りに90°回転することは、反時計回りに270°回転することと結果的には同じなのです。-90°だけ回転した位置と、270°だけ回転した位置が同じなのですね。ですから、__-180°より大きく、かつ0°未満のときには360°だけ足し、0°以上360°未満の範囲に直す__のが正解となります。問題点 その2
プレイヤーの向きを表す角度については検証できましたので、次は監視カメラの向きについてです。たとえば、次の例を考えてみましょう。
- 監視カメラの向きが10°、視野角が60°の場合、監視カメラの向きの範囲が-20°~40°になってしまうため、監視カメラの向きの範囲を0°~40°と340°~360°の2つに分けて判定する必要がある。
- 監視カメラの向きが350°、視野角が60°の場合、監視カメラの向きの範囲が320°~__380°__になってしまうため、監視カメラの向きの範囲を320°~360°と0°~20°の2つに分けて判定する必要がある。
……考えるだけで頭が痛くなるのですが、避けて通ることはできません。0°未満、または360°以上の場合もプレイヤーを視認できるか判定できるよう、処理を追加する必要があります。では、findPlayerメソッド内において、角度による判定を行う部分を次のように書き換えます。
public boolean findPlayer(Player player) { // 中略 // 角度による判定 double a = Math.toDegrees(Math.atan2(py - this.y, px - this.x)); if (a < 0) { a += 360.0; } System.out.println("a = " + a); double aMin = this.dirAngle - this.viewAngle/2; if (aMin < 0.0) { // カメラの向きの最小が負のときは,aMin+360~360の範囲で視認できるか判定する aMin += 360; if (aMin <= a && a < 360.0) { return true; } // 以後,aMin+360~360の範囲は考えなくて良い aMin = 0.0; } double aMax = this.dirAngle + this.viewAngle/2; if (aMax >= 360.0) { // カメラの向きの最大が360以上のときは,0~aMax-360の範囲で視認できるか判定する aMax -= 360.0; if (0.0 <= a && a <= aMax) { return true; } // 以後,0~aMax-360の範囲は考えなくて良い aMax = 360.0; } System.out.println("aMin = " + aMin + ", aMax = " + aMax); if (aMin <= a && a <= aMax) { return true; } return false; }問題点その1で説明したように、プレイヤーの向きを求めた後(変数a)、その値が負であれば360を足しておきます。これにより、プレイヤーの向きは必ず0°以上360°未満で表されることになります。
次に、カメラの向きの最小を求めた後(変数aMin)、その値が0°未満の場合はまずaMin + 360°以上360°未満の範囲でプレイヤーを視認できるかどうか判定し、視認できればtrueを返します(残りの処理をスキップします)。視認できなければ残りの範囲でも判定する必要がありますから、処理が続きます。なお、aMin + 360°以上360°未満の範囲についてはもう考える必要がないため、aMinを0°としています。これにより、後で0°以上aMax以下の範囲でも判定するようになっています。カメラの向きの最大(変数aMax)についても同様です。3.完成
ここまでの検証を反映させたプログラムです。長かった………
本当はもっと回り道してたし生まれ変わったプレイヤー視認プログラム(クリックすると開きます)
import java.util.Scanner; class CameraTest { public static void main(String[] args) { // 入力 Scanner sc = new Scanner(System.in); // プレイヤー double px = sc.nextDouble(); // プレイヤーのx座標 double py = sc.nextDouble(); // プレイヤーのy座標 Player player = new Player(px, py); // 監視カメラ int N = sc.nextInt(); // 監視カメラの台数 for (int n = 0; n < N; n ++) { // 監視カメラごとの入力・処理 double x = sc.nextDouble(); // 監視カメラのx座標 double y = sc.nextDouble(); // 監視カメラのy座標 double d = sc.nextDouble(); // 監視カメラが視認できる距離 double e = sc.nextDouble(); // 監視カメラの向き(direction)を表す角度 double f = sc.nextDouble(); // 監視カメラの視野角 Camera camera = new Camera(x, y, d, e, f); if (camera.findPlayer(player)) { System.out.println("視認できた"); } else { System.out.println("視認できなかった"); } } sc.close(); } } class Player { private double x; // プレイヤーのx座標 private double y; // プレイヤーのy座標 public Player(double x, double y) { this.x = x; this.y = y; } public double getX() { return this.x; } public double getY() { return this.y; } } class Camera { private double x; // 監視カメラのx座標 private double y; // 監視カメラのy座標 private double distance; // 監視カメラが視認できる距離 private double dirAngle; // 監視カメラの向き(direction)を表す角度 private double viewAngle; // 監視カメラの視野角 public Camera(double x, double y, double d, double e, double f) { this.x = x; this.y = y; this.distance = d; this.dirAngle = e; this.viewAngle = f; } public boolean findPlayer(Player player) { double px = player.getX(); double py = player.getY(); // 距離による判定 double d = Math.sqrt(Math.pow(this.x - px, 2) + Math.pow(this.y - py, 2)); if (d > this.distance) { return false; } // 角度による判定 double a = Math.toDegrees(Math.atan2(py - this.y, px - this.x)); if (a < 0) { a += 360.0; } System.out.println("a = " + a); double aMin = this.dirAngle - this.viewAngle/2; if (aMin < 0.0) { // カメラの向きの最小が負のときは,aMin+360~360の範囲で視認できるか判定する aMin += 360; System.out.println("aMin = " + aMin + ", aMax = 360.0"); if (aMin <= a && a < 360.0) { return true; } // 以後,aMin+360~360の範囲は考えなくて良い aMin = 0.0; } double aMax = this.dirAngle + this.viewAngle/2; if (aMax >= 360.0) { // カメラの向きの最大が360以上のときは,0~aMax-360の範囲で視認できるか判定する aMax -= 360.0; System.out.println("aMin = 0.0, aMax = " + aMax); if (0.0 <= a && a <= aMax) { return true; } // 以後,0~aMax-360の範囲は考えなくて良い aMax = 360.0; } System.out.println("aMin = " + aMin + ", aMax = " + aMax); if (aMin <= a && a <= aMax) { return true; } return false; } }findPlayerメソッドにおいて、プレイヤーの向きを表す角度を格納する変数aの値が負のときは、360を足す処理を追加しただけです。そして、リベンジ結果です。
10 16 8 270 120 a = 270.0 aMin = 210.0, aMax = 330.0 視認できたばっちりですね!
4.今回の教訓
挙げだせばキリがないのですが、今回特に足を引っ張った点について書いてみます。
他人がつくったものを使うときは、仕様を必ず調べる!
今回最大の反省点です。私は大昔にatan2メソッドのことを知り、そして今回久しぶりに使ってみた訳ですが、返り値については完全にスルーしていました。と言うより、0°以上360°未満で返してくるだろうと思い込んでしまっていたのです。また、思い込んでいたが故に、原因に気づくのにもかなりの時間をかけてしまいました。さらに白状するなら、atan2メソッドの引数は$y$成分、$x$成分の順に代入するのが正しいのですが、初めは逆に入れてしまっていました。ぐっだぐだです。
もしこれが開発の現場だったら、と考えると恐ろしいですよね。コンパイラは通ったけど正しい処理をしない、つくった自分は正しいと信じ込んでいる………。大惨事です。もちろん、責任はつくった私にありますから、何の言い訳もできません。
ということで、他人がつくったものを使うときは、その__仕様を必ず調べる__ことを徹底しましょう。今回のatan2メソッドについて言えば、引数に何が入るか、返り値はどのような値か、あるいはどのような範囲かを調べておく必要があります。その際、自分の思い込みは一切排除するようにしましょう。自分がつくったものを他人に使わせるときは、仕様を必ず明確にしておく!
これは今後の教訓としてです。複数人のチームで開発を行うとき、自分が担当するプログラムがどのような入力を想定していて、どのような処理を行って、どのような結果を出力するのか、きちんと整理しておく必要があります。自分が書いたプログラムの中にコメントとして残すか、あるいは別の書類として保存しておくか、現場により様々なルールはあると思いますが、どのような形にせよ必ず残しておきましょう(自分が作ったものですら、時間が経てば必ず忘れてしまいます!)。さもなくば、チームの仲間に大変な迷惑をかけることになります。
5.終わりに
先日、前編の記事を投稿した後、私が知らないメソッドや処理の方法をコメントで教えていただいて、非常に勉強になりました。今後もQiitaに記事を投稿していくとともに、いずれは自分もアドバイスできるよう頑張って参ります。
ここまで読んでくださって、ありがとうございました。