AtCoder 入茶しました

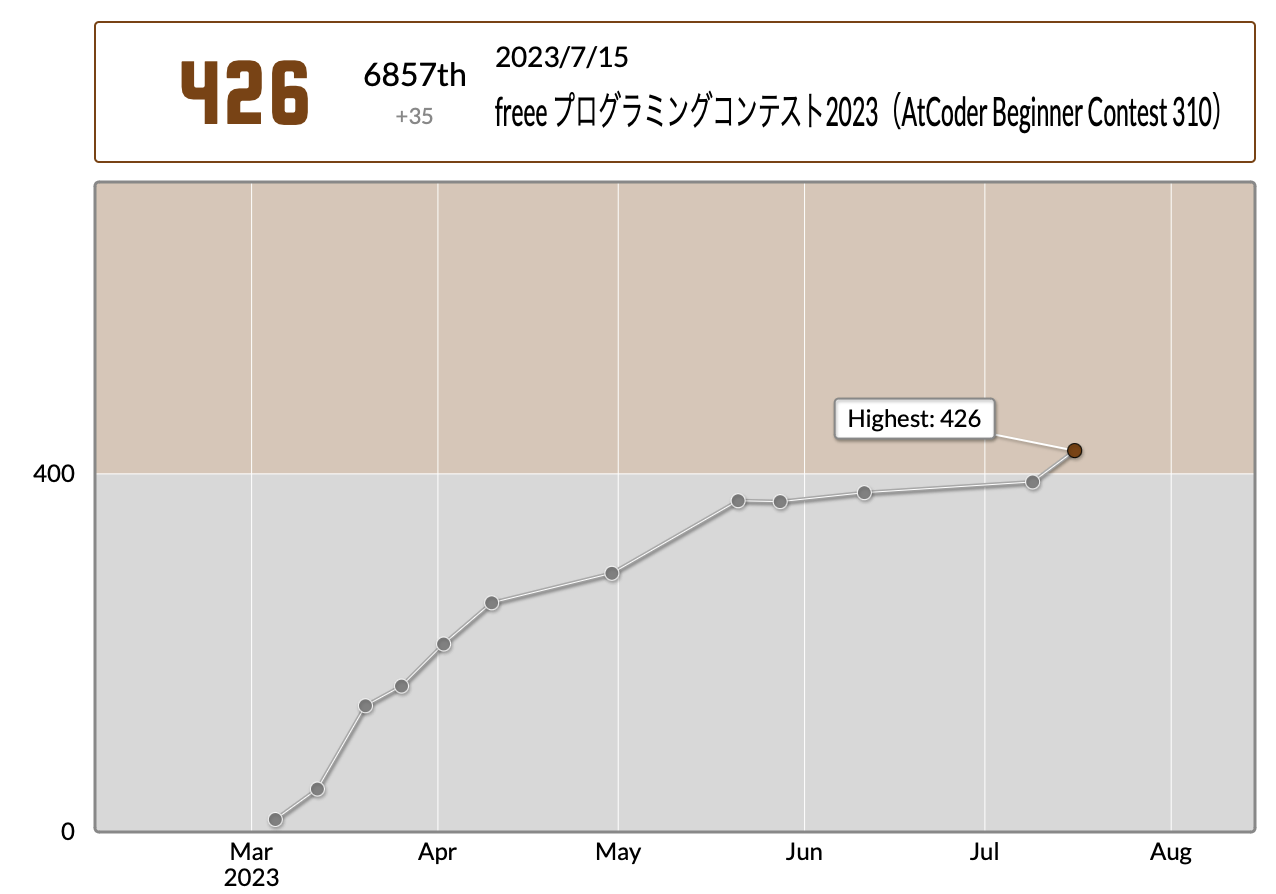
AtCoder入茶しました。なんか色変したら記事書く文化の様なので書きます。
ABC310にて、BでつまづいてAとCのみACで絶対スコア落としたと思ったのになんか入茶できました、逆に納得いかない。

前向きな勉強法とかこんなことしました的なのは多いので、自分は反省書いていきます。

問題文の読み違いをやらかす

AtCoderの問題文は丁寧に読めば論理的に解釈の余地が入るようなものはないです。しかし、制限時間付きでやってると問題文を斜め読みして、入出力サンプルをざっと見て、憶測の入った解釈で解答に臨んでしまうことも多く、実際それでも9割ぐらいは正答できるんですが、やっぱり1割ぐらいはなんか勘違いや読み違いをしてしまうもので、その間違った解釈でコードを書き、WAでもコードが間違ってるんだと思って何度やっても通らない修正を繰り返してしまうというパターンに数度ハマりました。おおよそコードが思った通りに書けているのにサンプルすら正答にならないなら問題文を読み直すべきでした。
プログラマーが最も学ぶべき言語は日本語というのは至言です。

直近のやらかし案件です
ABC309 B
全部の要素を時計回りにするのだと勘違いしました、B問題のクセに結構面倒なの来たなと思いました。サンプルすら通らなくて1時間近く四苦八苦してました、丁寧にコードを読み返してみても意図通りに書けてる、それで問題文を読み間違ってる可能性に思い当たって読み直したらやっぱり間違ってました。
一番外側だけ時計回りにすればよかったんです、問題文を正しく読めたら数分でした。
次のABC309 Cでも「初日から条件を満たしているパターン」をカバーできていなくて何度かWAしちゃいました。こっちは単に想像力不足でした。

うっかりミスをやらかす

コードが少し長くなっただけで、スペルミスとか変数名を意図せず重複させてしまったりとか、しっかりコードを読み直せばわかるようなミスで落とすことが多いです。
人間、PCのメモリと同様に、一度に記憶・思考できる量の限界はあるもので、書いたコードを読んでいて、脳内のデータの状態のシミュレーションが追いつかなくなってくると、軽くパニック状態になってうっかりミスも増えてきます。
自分はこの辺のスペックが高くないので、if,for,whileが6つぐらい組み合わさってくるともう頭の中のデータ状態のシミュレーションが追いつきません、その処理にどういう値が渡されうるかのイメージが正確にできなくなってしまいます。
また、TLEの原因になるだろう非効率な処理を見つけて途中でやり方を変えるということも頻繁にあり、この時にコードの修正箇所が漏れているということもちょくちょくあります。
ここは何かやる時の方法に型がなくて、行き当たりばったりでやってるせいで、考えるべき可能性が多くなってしまっているのも要因かなと思ってます。関数化するのかクラス書くのか、オブジェクトでやるのか配列でやるのか、その構造はどうするのか、とにかく行き当たりばったりでブレブレ、パターンがないからどういう時に何に気をつければいいのかといった学習もなかなか積み上がらない。　
それぞれのケースに合わせて最適なものを選ぶというのも大切かと思いますが、どっちでもいいものについてはどっちにするか方針を決めておいて、迷わないようにしておくのも大事かなと思います。

直近のやらかし案件です
ABC310 B
AtCoderの問題では数値をフラグの集合として扱うということをちょくちょくやることになります。フラグの数が63以下ならintで、64以上ならgmpでやる感じなんですが、gmp_initで第一引数の文字列を２進数として扱う指定をしていない、インデックスが1~100なら文字列は101桁必要といった基本的なことをうっかりしてテストケース２つがWA、これに気づかず１時間近く違うところばっかり見て修正で四苦八苦、諦めてC問題を先にAC、時間的にD問題を諦めてBに戻るも、またもうっかりに気づかず時間切れ、翌日見直したらコードの冒頭でやらかしてるのに気づいて手遅れのAC。

PHPer @ AtCoder

AtCoderはPHPerが少ないですね、PHPer人口はそれなりいると思うのに。
たかだか茶色がおこがましいですが、PHPerの参加を促すためにPHPでAtCoderやるにおいて、抑えておきたいポイント書いておきます。

gmpライブラリは必須

AtCoderの問題では、64bitを超える整数値を扱うことがちょくちょくあります。gmpはそういう数値を扱う際に必須です。関数も様々用意されています、PHPでAtCoder挑戦する際に抑えておきたい関数は以下。

乗算・除算

gmp_div_qr — 除算を行い、商と余りを得る
gmp_gcd — 最大公約数を計算する
gmp_lcm — 最小公倍数を計算する

べき乗・階乗・平方

gmp_sqrt — 平方根を計算する
gmp_pow — べき乗を計算する
gmp_powm — べき乗とモジュロを計算する
gmp_fact — 階乗
gmp_perfect_power — 累乗数かどうかを調べる
gmp_perfect_square — 平方数かどうかを調べる

ビット

gmp_and — ビット AND を計算する
gmp_or — ビット OR を計算する
gmp_xor — ビット XOR を計算する
gmp_setbit — ビットを設定する
gmp_testbit — ビットが設定されているかどうかを調べる
gmp_scan0 — 0 を探す
gmp_scan1 — 1 を探す
gmp_popcount — セットされているビットの数

文字列操作系の関数でよく使うもの

preg_replace_callback - 正規表現検索を行い、コールバック関数を使用して置換を行う
substr - 文字列を切り出し
strrev - 文字列を反転
strtr - 文字を置き換え

エラトステネスの櫛・バイナリサーチ・素因数分解の関数は用意しておく

素数云々の問題は大体エラトステネスの櫛を使うことになります、すぐにコピペできるようにしておくのが吉です。捻くれている自分は、「5以上の素数は6n-1か6n+1にしかないんだからこっちの方が効率的でしょ」というような作り方をしてます。

function get_primes($lt){
	$flags=[2=>true,3=>true];
	for($i=5;$i<=$lt;$i+=6){
		$flags[$i]=true;
		$flags[$i+2]=true;
	}
	if($i-4>$lt){unset($flags[$i-4]);}
	$max=sqrt($lt);
	foreach($flags as $n=>$f){
		if($n>$max){break;}
		for($m=$n*5;$m<$lt;$m+=$n){
			if(isset($flags[$m])){unset($flags[$m]);}
		}
	}
	return array_keys($flags);
}

バイナリサーチは整列済みの数値の配列から効率的に値を探索するための処理です。
ある数値が配列のどの数値と数値の間に位置するかを探索するのにも使います。
整列済みの数値の配列を扱う問題でarray_searchとかしてたら大体TLE（処理時間オーバー）です、バイナリサーチの関数を用意しておきましょう。

function bsearch($arr,$val){
	$n=0;
	if($val>end($arr)){return count($arr);}
	if($val<reset($arr)){return -1;}
	for($r=(count($arr)>>1);$r>0;$r>>=1){
		if($val===$arr[$n+$r]){return $n+$r;}
		if($val>$arr[$n+$r]){$n+=$r;$r++;}
	}
	return $n;
}

gmpには最大公約数・最小公倍数を求める関数があるのに素因数分解の関数はないです。今のところ自分は使う場面がなかったんですが、多分必要になることがあるはず、用意しておいた方がいいと思います。

function get_prime_factors($n){
	$rtn=[];
	if(($n&1)===0){
		$n>>=1;$rtn[2]=1;
		while(($n&1)===0){$n>>=1;$rtn[2]++;}
	}
	if($n%3===0){
		$n/=3;$rtn[3]=1;
		while(($n%3)===0){$n/=3;$rtn[3]++;}
	}
	$max=sqrt($n);$i=0;
	for($m=5;$m<=$max;$m+=($i++&1)?2:4){
		if($n%$m===0){
			$n/=$m;$rtn[$m]=1;
			while(($n%$m)===0){$n/=$m;$rtn[$m]++;}
			$max=sqrt($n);
		}
	}
	if($n>1){$rtn[$n]=1;}
	return $rtn;
}

以上です　

このままだと緑色変の記事を書くことは多分ない気がします　(´・ω・｀)