はじめに
Prologで一筆書きをするプログラムを書きました。
オイラーの定理
ケーニヒスベルクの橋の問題はポピュラーです。数学者オイラーはグラフ理論におけるオイラーの定理を証明し、ケーニヒスベルクの橋の問題は解決しました。次の図形はオイラーの定理によれば一筆書きができるはずです。
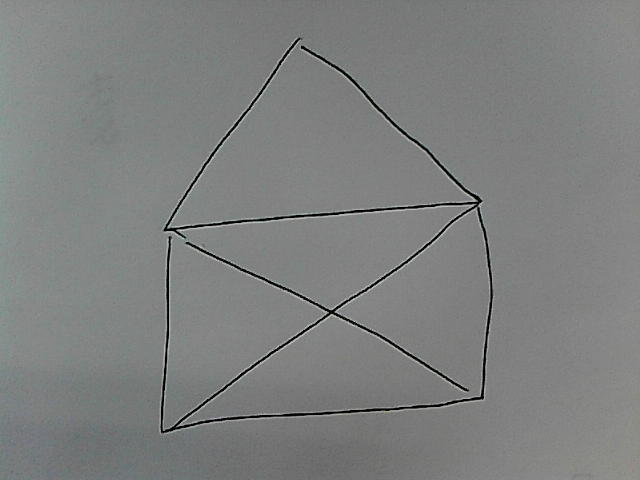
これをPrologで解いて楽しみましょう。
アイディア
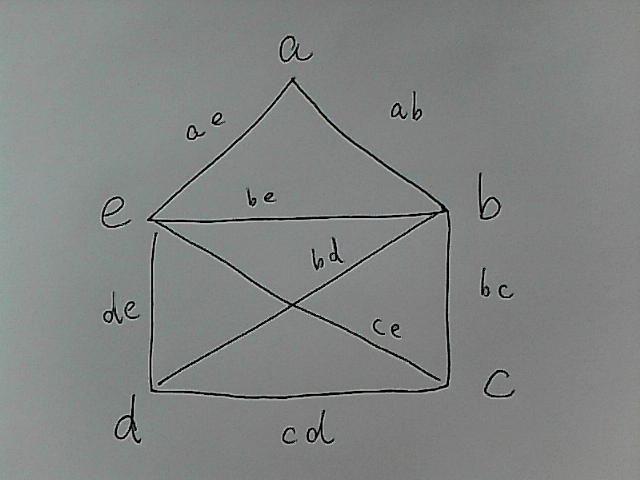
頂点と辺に次の図のように名前をつけました。
すべての辺をリストにして初期値とします。移動可能なルートをroot/3として記憶しておきます。
root(a,b,ab).
これは頂点、a,bが辺abによりつながることを意味しています。移動可能なルートをバックトラックによりしらみつぶしに調べます。このとき通過した辺は辺のリストから削除します。辺のリストに移動しようとしている頂点への辺が存在しなければ失敗します。他のルートを当たることになります。最終的にすべての辺を通過し辺のリストが[]になったときが一筆書きが成功した場合です。このときにはその追加してきた頂点のリストを画面出力します。
実行結果
O-Prolog Ver 1.62(Chika)
| ?- ['one-stroke.pl'].
yes
| ?- run.
[c,e,a,b,c,d,e,b,d]
[c,e,a,b,c,d,b,e,d]
[c,e,a,b,d,e,b,c,d]
[c,e,a,b,d,c,b,e,d]
[c,e,a,b,e,d,b,c,d]
[c,e,a,b,e,d,c,b,d]
[c,e,b,c,d,e,a,b,d]
[c,e,b,c,d,b,a,e,d]
[c,e,b,d,e,a,b,c,d]
[c,e,b,d,c,b,a,e,d]
[c,e,b,a,e,d,b,c,d]
[c,e,b,a,e,d,c,b,d]
[c,e,d,b,e,a,b,c,d]
[c,e,d,b,a,e,b,c,d]
...
[d,c,e,d,b,a,e,b,c]
[d,c,b,d,e,a,b,e,c]
[d,c,b,d,e,b,a,e,c]
[d,c,b,e,a,b,d,e,c]
[d,c,b,e,d,b,a,e,c]
[d,c,b,a,e,b,d,e,c]
[d,c,b,a,e,d,b,e,c]
yes
dかcからスタートする場合だけしか一筆書きができないようです。手で書いてみていくつか確かめました。全部は確認していないのですが、良さそうな感じです。
コード
Prologだと短い行数で書けてしまいます。この手の問題に向いています。これをC言語などで記述しようとすると、けっこう手間がかかると思います。
root/3 頂点と辺のデータ
run/0 メイン述語
node/1 すべての頂点のリスト
edge/1 すべての辺のリスト
solve/1 リスト中のすべての頂点からスタートして一筆書きができるかどうかを調べ、可能なら表示する。
solve1/3 第一引数をスタート地点、第二引数を辺のリストとして、一筆書き可能なら表示する。バックトラックにより網羅する。
delete/3 第一引数のリストから第二引数を削除したものを第三引数にunifyする。削除するものがない場合には失敗する。
root(a,b,ab).
root(b,c,bc).
root(b,d,bd).
root(b,e,be).
root(c,e,ce).
root(c,d,cd).
root(d,e,de).
root(e,a,ae).
node([a,b,c,d,e]).
edge([ab,bc,bd,be,ce,cd,de,ae]).
run :- node(N),solve(N).
solve([]).
solve([N|Ns]) :-
edge(E),solve1(N,E,[N]).
solve([N|Ns]) :-
solve(Ns).
solve1(X,[],R) :- reverse(R,R1),write(R1),nl,fail.
solve1(X,E,R) :-
root(X,Y,E1),
delete(E,E1,E2),
solve1(Y,E2,[Y|R]).
solve1(X,E,R) :-
root(Y,X,E1),
delete(E,E1,E2),
solve1(Y,E2,[Y|R]).
delete([X|Xs],X,Xs).
delete([X|Xs],Y,[X|Z]) :-
delete(Xs,Y,Z).