はじめに
Pascalの本にあった経路探索の問題を解きました。Prologにおける典型的な応用例です。
問題
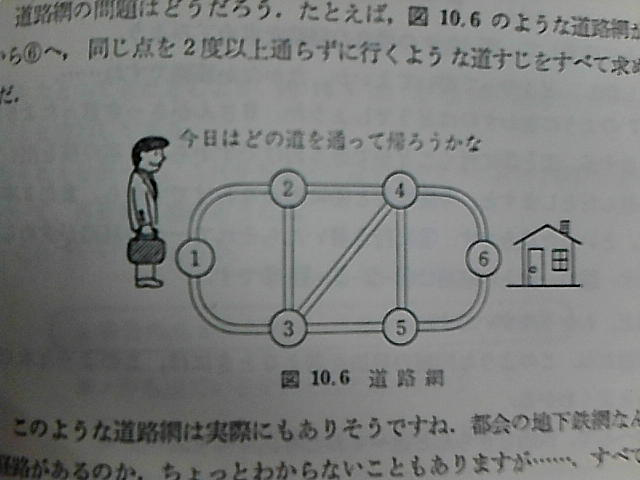
図のような道路網があったときに、1から6へ、同じ点を2度以上通らずに行くような道筋をすべて求めよ、という問題です。
PascalとPrologの対比
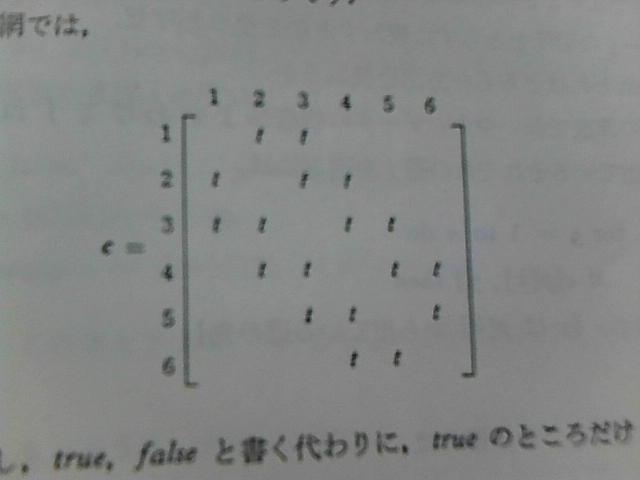
Pascalの回答例では隣接行列を用いていました。隣接行列とは図のようなもので、道のつながり具合を示したものです。
Pascalの場合には、この隣接行列によるのが一般的だろうと思います。Prologの場合には述語で道路を表すことができます。
root(1,2).
無向グラフのようなものです。2から1へも移動できます。1,2を逆にして判定すれば簡単ですね。
コード
ということで、Prologで書くとあっさりと書けます。下記の通りです。
root(1,2).
root(1,3).
root(2,3).
root(2,4).
root(3,4).
root(3,5).
root(4,6).
root(4,5).
root(5,6).
run :- solve(1,[1]),fail.
solve(6,R) :- reverse(R,R1),write(R1),nl.
solve(N,R) :-
root(N,O),
\+(member(O,R)),
solve(O,[O|R]).
solve(N,R) :-
root(O,N),
\+(member(O,R)),
solve(O,[O|R]).
実行
実行すると次のようになります。
| ?- ['keiro.pl'].
yes
| ?- run.
[1,2,3,4,6]
[1,2,3,4,5,6]
[1,2,3,5,6]
[1,2,3,5,4,6]
[1,2,4,6]
[1,2,4,5,6]
[1,2,4,3,5,6]
[1,3,4,6]
[1,3,4,5,6]
[1,3,5,6]
[1,3,5,4,6]
[1,3,2,4,6]
[1,3,2,4,5,6]
no
Prologの特長
バックトラック、ユニフィケーションがPrologの特長です。これらが活かせる問題のときには無類の強さを発揮します。
終わりに
しばらくPrologを離れることになりました。Elixirに集中します。LispもPrologも素晴らしいプログラミング言語です。しかし、それはラテン語のような存在です。計算機科学を習得するにはいずれも必須だと私は考えています。一方、現代におけるモダンなプログラミング言語で現実のプログラミングに挑戦してみたいと思っています。Lisp・Prologの習得で学んだことを活かしてみたいと思っています。今までお読みいただきありがとうございました。
丹下のおっさん、燃え尽きたぜ…真っ白にな…