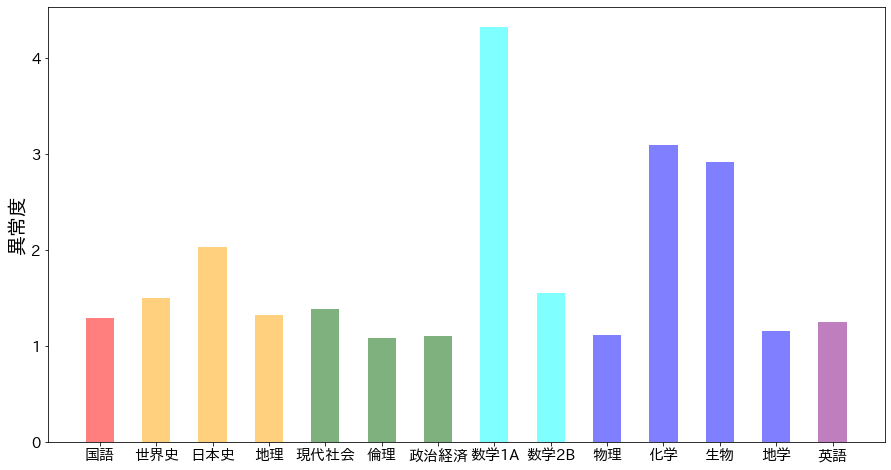はじめに
2022年1月に行われた大学入試共通テストは、1990年より行われていた大学入試センター試験が2021年に大学入試共通テストへと移行してからの2回目の試験となりました。
これまでのセンター試験が事実上暗記で解ける問題も多い試験形式となっていたり、また過去30年に渡り運用されたことで対策され尽くしている(?)状況を踏まえ、大学入学共通テストは思考力、判断力、表現力等を発揮して解くことが求められる問題を重視する試験形式となったようです。
しかしまだ移行してから2年目であり、作問側も手探りの状態なのか、難易度が安定せず昨年に比べて大幅に難化したと報道されています。
特に、主要科目の一つであり選択する受験生も多い数学1Aについては、前身のセンター試験の時代から数えても最も平均点が低くなり、関係者からも難易度について疑問の声が上がる状況となっているようです。
そこでこの記事では、2022年度の数学1Aが実際どの程度難しかったのか、過去の傾向や他科目との兼ね合いから定量的に考察してみます。
もちろん、"平均点が過去最低である"というのは難しさの指標のひとつですが、それだけが難しさを記述するものではありません。
年度ごと、科目ごとに難易度の変化やばらつきがある中で、今回の数学1Aは
- 平均点は過去最低であったが、他の科目も同様に難しくそれらと比べ難易度が抜きん出ているものではない
- 確かに難しく、それは他の科目の平均点の低下を差し引いてもなお突出したものである
のどちらのケースに相当するのか気になったので、以下で検証します。
今回用いたデータ
具体的な考察に入る前に、今回用いるデータについて説明します。
- 対象データ:大学入試センター公表の平均点(センター試験はここ、共通テストはここ、およびここを参照しました。)
- 対象科目:国語、世界史B、日本史B、地理B、現代社会、倫理、政治経済、数学1A、数学2B、物理、化学、生物、地学、英語の計14科目
- 対象年度:1990年度(平成2年度)から2022年度(令和4年度)の計33年間
なお、この記事では実際に問題を解いてみたり、問題の構成を検討したりといった、問題の中身に立ち入った議論は行いません。
あくまで科目ごとの平均点の変遷という立場のみから難易度を議論します。
「結果だけ見たい!」という方はこちらに飛んでください。
データに関する注意点
今回用いたデータに関する注意点をまとめます。
- 記事執筆の2022年2月5日時点で、2022年度の確定した平均点は公表されていないため、2022年1月19日発表の中間集計の値を用いました。
- 全ての点数は100点満点に換算した値です。
- 英語のリスニングは2005年度以前は実施されていないため、今回の検証からは除外しました。
- 1996年度以前は倫理と政治経済が同一の科目となっているため、1996年度までは両者には同一の点数を割り振りました。
- 科目によっては同一年度内でさらに細分化されているものがありますが(物理IAと物理IB、物理基礎と物理、など)、それぞれの年度で最も受験者が多い科目を対象としました。
平均点の推移
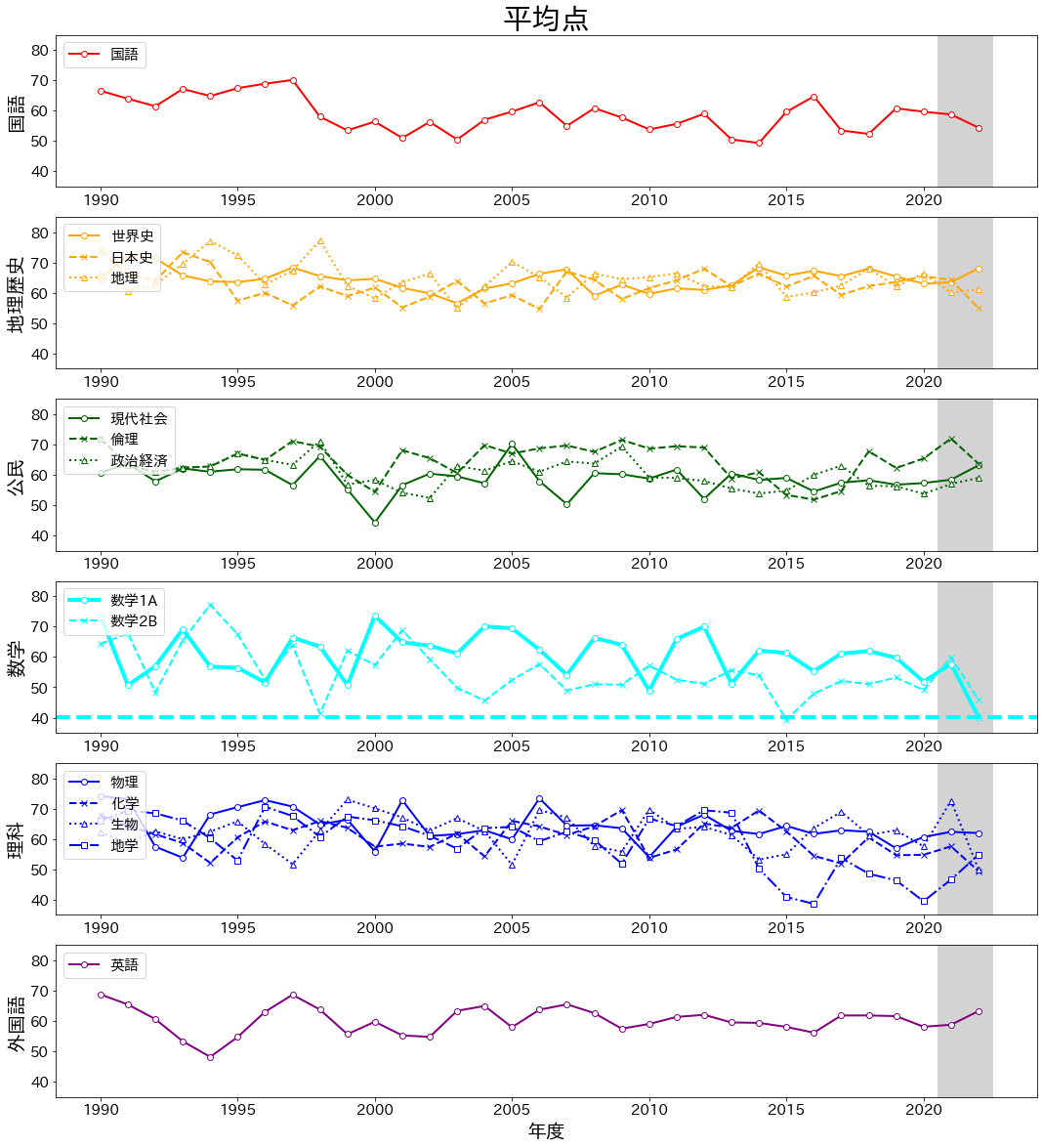
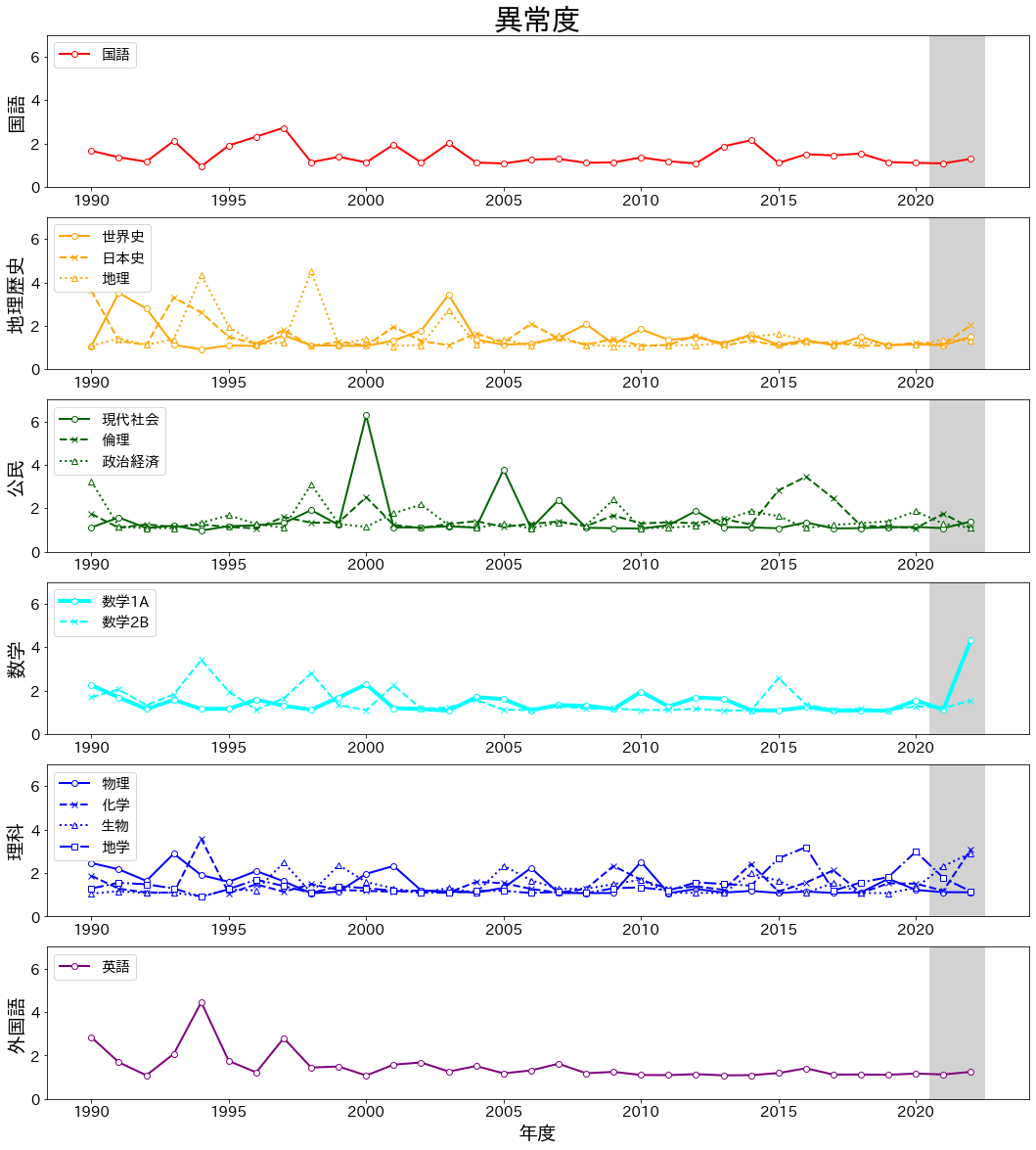
まずデータの雰囲気を掴むため、以下に各科目の平均点の推移(1990年度~2022年度)を図示します。
視認性のため、国語・地理歴史・公民・数学・理科・外国語でパネルと色を分けました。
なお、グレー背景が大学入試共通テストの期間です。
こうして見ると科目によって様々な変遷があり面白いですね。
そして、確かに2022年度は数学1Aが過去最低点であること(シアンの水平線)がわかります。
しかし、他にも2021年度に比べ大幅に難化している科目が見受けられます(数学2B、生物など)。
繰り返しになりますが、ここでの興味は過去や他科目との関係も加味した上で、数学1Aの難易度がどの程度特異かです。
その検証のため、以下で述べるようにガウスグラフィカルモデルを用いた方法を採用し、分析を行います。
科目平均点間の構造学習を経た異常度の考え方
ここでは、ガウスグラフィカルモデルを用いて数学1Aの難易度がどの程度異常であったのかを定量化するための考え方を説明します。
以下の記述では、井手剛先生・杉山将先生著「異常検知と変化検知」を参考にさせていただきました。
また、そのコーディングに関してはこちらの記事を参考にさせていただきました。
構造学習の考え方
構造学習とは、変数(今回は科目)間の関係に確率モデルを仮定し、変数間の構造をそれを用いて表現する手法です。
仮定された確率モデルはデータから学習されます。
以下では、科目間の確率分布に多変量正規分布(ガウス分布)${\it N}(\boldsymbol{x}|\boldsymbol{\mu}, \Sigma)$を仮定します。
ここで、$\boldsymbol{x}=(x_{1}, ..., x_{M})$は注目する年の科目の平均点を並べたベクトルで、次元数は$M=14$です。
また$\boldsymbol{\mu}$は全年度に渡る科目ごとの平均点の平均ベクトル(ややこしいですが...)、$\Sigma$は科目の分散共分散行列です。
\begin{align}
{\it N}(\boldsymbol{x}|\boldsymbol{\mu}, \Sigma) = \frac{1}{(2\pi)^{M/2}|\Sigma|^{1/2}}\exp{\left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T}{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right)} \tag{1}
\end{align}
ここで、ベクトル$\boldsymbol{x}$は平均0、分散1に標準化されているとします。
ゆえに$\boldsymbol{\mu}=0$であり、分散共分散行列$\Sigma$は変数間の相関係数行列と等しくなります。
さて、この相関係数行列$\Sigma$をデータから計算するのですが、$\exp$の肩に現れているのはその逆行列なので、精度行列$\Lambda = \Sigma^{-1}$を定義し、以降はこの導出に注目します。
なお、詳細は省きますが、確率モデルに多変量正規分布を仮定する場合、
- 分散共分散行列(相関係数行列)$\Sigma$:変数間の直接相関+間接相関を表す
- 精度行列$\Lambda$:変数間の直接相関のみを表す
という著しい性質があるため、精度行列を計算すると変数間の相関の正体についての見通しが非常に良くなるというメリットがあります。
疎構造学習の手法
さて、以降求めたいものは精度行列$\Lambda$であり、それはただ単に相関係数行列$\Sigma$の逆行列を求めれば良いのですが、ここで少しの工夫を加えると導出された精度行列$\Lambda$がより好ましい性質を持ちます。
その工夫とは、精度行列$\Lambda$にスパース性を与え、最大事後推定(MAP推定)により推定するというものです。
参考文献にわかりやすく記述されていますが、この手法は
- 逆行列の直接計算を行わず、また正定値性を損なわずに精度行列$\Lambda$が推定可能
- 直接相関の低い変数間の相関を刈り落とすことで、変数同士の関係の見通しが良くなり、かつノイズに対して頑健になる
などのメリットを持ちます。
具体的には、精度行列の事前分布にラプラス分布
\begin{align}
p(\Lambda) = \frac{\rho}{2}\exp(-\rho||\Lambda||_{1}) \tag{2}
\end{align}
を仮定した上で、精度行列$\Lambda$を最大事後推定
\begin{align}
\Lambda^{*}
&= arg max_{\Lambda} \left(\ln{p(\Lambda)}\prod_{n=1}^{N}{\it N}(\boldsymbol{x}|\boldsymbol{0}, \Lambda)\right) \\
&= arg max_{\Lambda} \left(\ln{{\rm det}\Lambda} - {\rm tr}(SA) - \rho||\Lambda||_{1}\right) \tag{3}
\end{align}
を経て求めます。
ここで、$\rho$は正則化の強さを表す非負の実数で、$S$はデータの標本分散共分散行列(各科目が正規化されているため標本相関係数行列に等しい)です。
数式から明らかなように、ラプラス分布を事前分布として与えるMAP推定が、$\Lambda$に対する$L_{1}$正則化と等価となっていることがポイントです。
この性質から、ラプラス分布を事前分布として与えるなどしてスパース性を要求したグラフィカルモデルをグラフィカルラッソと呼びます。
推定された構造を用いた異常検知の手法
さて、これまでに述べたグラフィカルモデルの利点の一つに、異常検知への応用可能性が挙げられます。
ここでいう異常検知とは、今の文脈ではある科目の平均点が、他の科目とのこれまでの相関を壊すほど高すぎる/低すぎることの検知に相当します。
つまりグラフィカルモデルは、単にデータの値自体の大小ではなく、精度行列$\Lambda$を媒介することで、変数間の関係の崩れを検知することを可能とします。
加えて、その年度の平均点$\boldsymbol{x}$が科目全体として正常か異常かではなく、変数(科目)ごとの異常度を算出することが可能です。
今回、数学1Aがどの程度難しかったかを考察するにあたって、グラフィカルモデルを用いた理由の一つがこれです。
学習データより導出された精度行列$\Lambda$(($i, j$)成分を$\Lambda_{i, j}$で表す)、新たに得られた異常を判定したいデータ$\boldsymbol{x^{\prime}}$について、科目$i$の異常度は
\begin{align}
a_{i}(\boldsymbol{x}^{\prime})
= \frac{1}{2}\ln{\frac{2\pi}{\Lambda_{i, i}}}
+ \frac{1}{2\Lambda_{i, i}}\left(\sum_{j=1}^{M}\Lambda_{i, j}x_{j}^{\prime}\right)^{2} \tag{4}
\end{align}
で与えられます。
ここまでの計算で、直接相関のない科目$i$と科目$j$の間では$\Lambda_{i, j}=0$となるため、式(4)の右辺第2項から、科目$i$の異常度を算出する際は、それと直接相関のある科目$j$の影響のみが取り込まれることがわかります。
参考文献から言葉を拝借しますと、上式の異常度はいわば**「他の変数からの期待をどの程度裏切っているかの度合い」**を示す量となります。
直接相関がなければ、他の変数からの期待もないので、他の変数の挙動は異常度に勘定されないということです。
センター試験/共通テストに構造学習の手法を適用する
さて、いよいよ上で述べた手法を今回のケースに適用します。
2022年度の異常度の計算
標本相関係数行列の可視化
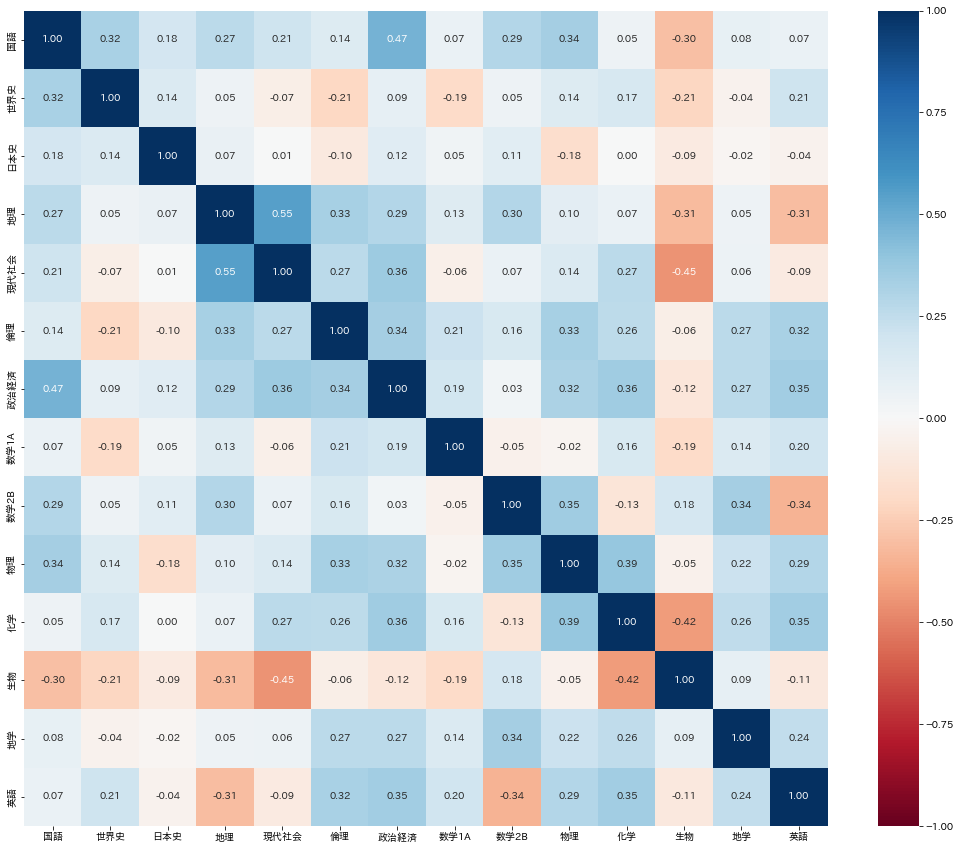
まずは、データの性質を掴むため学習に使う1990~2021年度までのデータの標本相関係数行列を可視化します。
正が青、負が赤に対応します。
"試験の点数には「学力」なる共通因子が存在する"といったように問題を極めて単純化して考えると、相関は正が多くなると予想できます。
おおむねその通りですが、一部負の相関を持つものもあるようです(生物と現代社会など)。
また、("数学力"という共通因子を持つと思われる)数学1Aと2Bに特に相関が見られないのも興味深いです。
おそらく、年度によって数学1Aと2Bの間にも難易度の高低があるのでしょう。
さて、状況が分かったところで、次に進みましょう。
正則化係数の決定
MAP推定の式に出てくる$L_{1}$正則化項のパラメータ$\rho$は理論的には与えられず、手で与えなければいけません。
しかしどんな値でもいいというわけでもないので、ここでは以下で与えるベイズ情報量基準(BIC)を最小化する$\rho$を求めます。
\begin{align}
{\rm BIC} = -2*\ln{L} + k*\ln{n} \tag{5}
\end{align}
ここで$L$はそのモデルの元での尤度、$k$はモデルの自由度の数、$n$はデータの観測数(今回は33-1=32)です。
BICは小さいほど真のモデルを記述する性質を持つことで知られます。
所与のデータに対するモデルの説明能力が上がると右辺第1項が小さくなりますが、モデルのパラメータを無闇に増やすことを抑制するため右辺第2項でペナルティを与えています。
モデルを複雑にし過ぎない程度に真のモデルに近づける、というわけです。
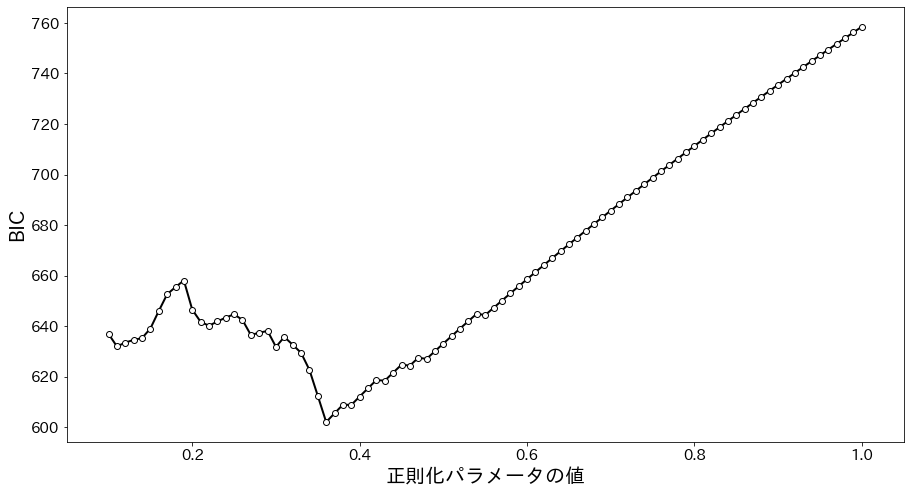
今回の学習データ(1990~2021年度の平均点)に対して、$\rho$を0.10から1.00まで0.01刻みで変えてBICを計算したのが以下のグラフになります。
図から$\rho=0.36$でBICが最小になっているので、以降はこれを用いて計算を進めます。
なお、$\rho=0$は正則化をしないことを意味します。
この場合、精度行列$\Lambda$は単純に標本相関係数行列$S$の逆行列となり、一般に解はスパースにはなりません。
一方$\rho$が大きくなり過ぎると、変数間の直接相関を全て刈り落としてしまいます。
実際、$\rho\sim0.5$を超えると、精度行列$\Lambda$の非対角成分が全て0となりました。
スパース性を取り込んだ精度行列
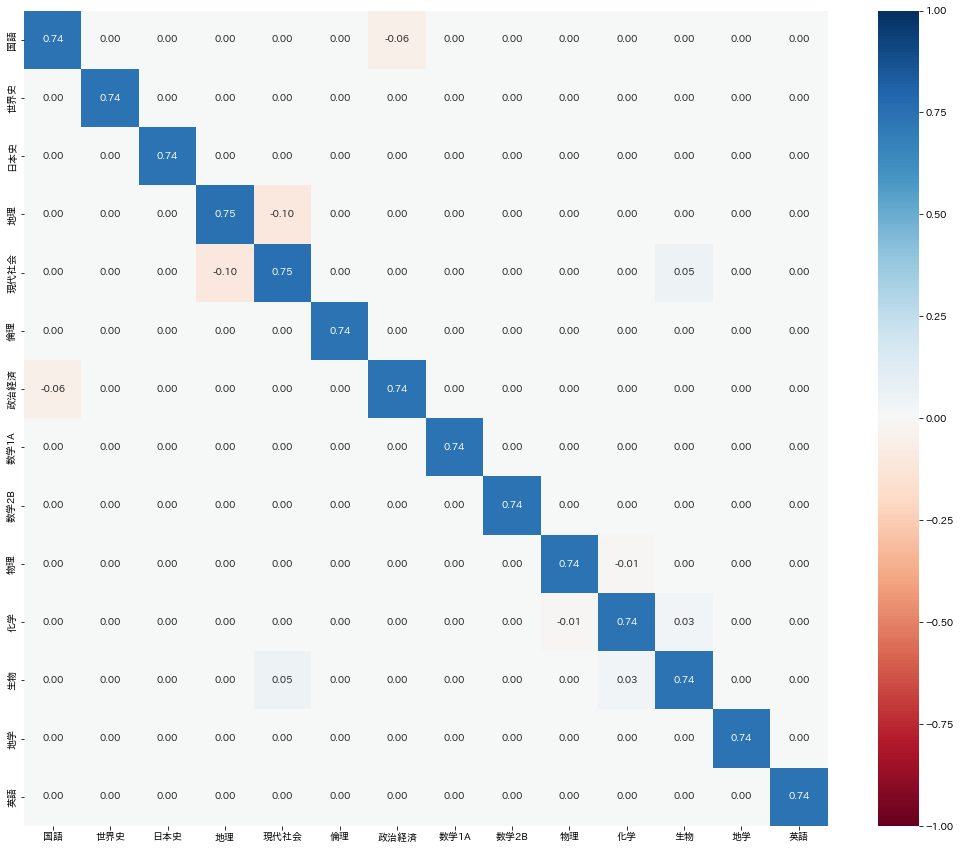
上で求めた$\rho=0.36$を適用しスパース化した精度行列$\Lambda$を図示します。
国語と政治経済、地理と現代社会、現代社会と生物以外の直接相関が消えているのがわかります。
(上で指摘した通り、間接相関まで含めると科目間の相関はこの限りではありません。)
科目ごとの異常度
さて、精度行列$\Lambda$が求まったので、いよいよ2022年度の科目ごとの異常度を、式(4)に基づいて計算します。
結果は以下です。
確かに数学1A(平均点40.25)の異常度(4.32)が突出しており、今年の科目の中では最も難しかったと推定されます。
これは、報道にあるような実際に受験した学生さんの感覚とも合致しています。
ちなみに、図より、化学(平均点49.45)や生物(同50.08)もそこそこ難しかったことがわかります。
一方で、2022年度では数学1Aに次いで平均点が低かった数学2B(同45.89)は、例年の傾向や他科目との関係からそこまで目立った難しさではないこともわかります。
他の科目との直接相関構造を加味することで、このように単純な平均点の大小を超えた議論ができることが興味深いです。
年度ごとの異常度の推移の計算
ここまでで、2022年度の数学1Aは、科目間の関係性を加味しても確かに難しいものであった、とわかりました。
一方で、このように特定の科目が突出して高い(もしくは低い)難易度を持つことはこれまでの歴史の中でなかったのでしょうか。
最後に、これまで述べた手法を応用し、各年度ごとの科目ごとの異常度の推移を計算してみます。
ここでの学習データは、異常度を計算する年度以外の全てのデータです。
つまり、例えば2000年度の科目ごとの異常度を計算したい場合、学習データは1990~1999, 2001~2022年度のデータとなります。
結果を以下に示します。
前節で述べた通り、2022年度では数学1Aの異常度(4.32)が突出しています。
これは、数学1Aの歴代の中で最も高い数値です。
一方で、対象を過去の他の科目まで広げると、
- 1994年度地理(平均点77.05、異常度4.34、易し過ぎた?)
- 1994年度英語(平均点48.21、異常度4.54、難し過ぎた?)
- 1998年度地理(平均点77.20、異常度4.51、易し過ぎた?)
- 2000年度現代社会(平均点44.30、異常度6.27、難し過ぎた?)
など、2022年度の数学1Aを超える特異度を持つ科目が、難化のみならず易化も含め過去に存在したこともわかります。
(科目の未来の平均点を用いて過去を計算するというある意味でズルをしているので、あくまで事後的に分かることですが...)
難化に比べ易化に関してはあまり報道で取り上げられることもないかと思いますが、本モデルではこのようにしてしっかり検知されます。
(受験者間で差をつけるべき入試問題において、平均点が8割弱というのはそれはそれで問題かもしれません。)
まとめ
ガウスグラフィカルモデルとスパースモデリングを組み合わせ共通テスト科目間の構造を学習することで、センター試験/共通テストの各年度、各科目ごとの平均点の異常度を計算してみました。
結論として、
- 2022年度の中では数学1Aの難易度は突出していた
- これは、1990年度まで遡っても、数学1Aの歴史に類を見ない難易度であった
- 一方で、過去の他科目を見ると、それ以上に特異な難化/易化を示す科目もあった
ということがわかりました。
私も昔センター試験を受けましたが、今振り返ってその年の特徴はどうかを考えるのも楽しいですね。
引き続き受験シーズン真っ只中なので、受験生の皆様のご健闘を応援しつつ、まとめとします。