はじめに
2021年3月のNHK世論調査にて、内閣支持率は支持が40.3%、不支持が36.5%(有効回答数1237)となり、それを受けての記事で「(3か月ぶりに)支持が不支持を上回りました」との記述がありました。(記事はこちら)
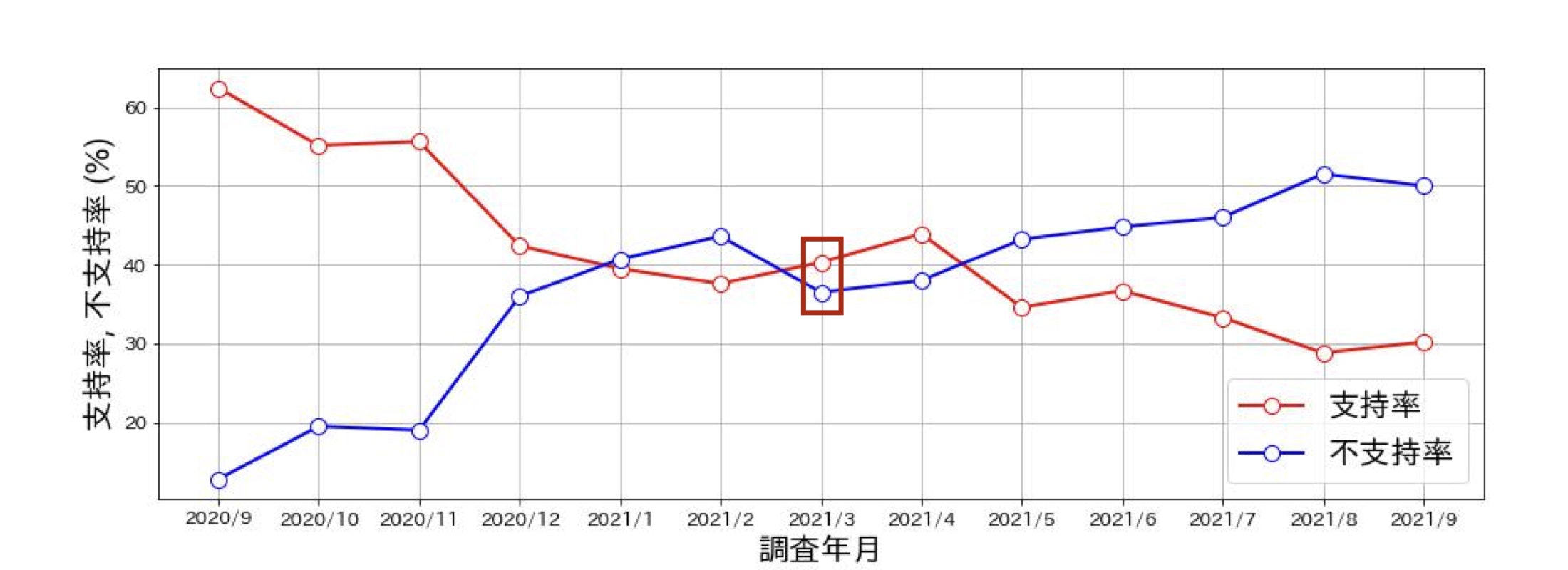
以下の図は菅内閣の2020年9月から2021年9月までの支持率と不支持率の変遷です。
2021年3月を見ると、確かに数字自体は支持のほうが大きく、その差は3.8%ですが、これは統計的にどの程度確からしいのでしょうか。
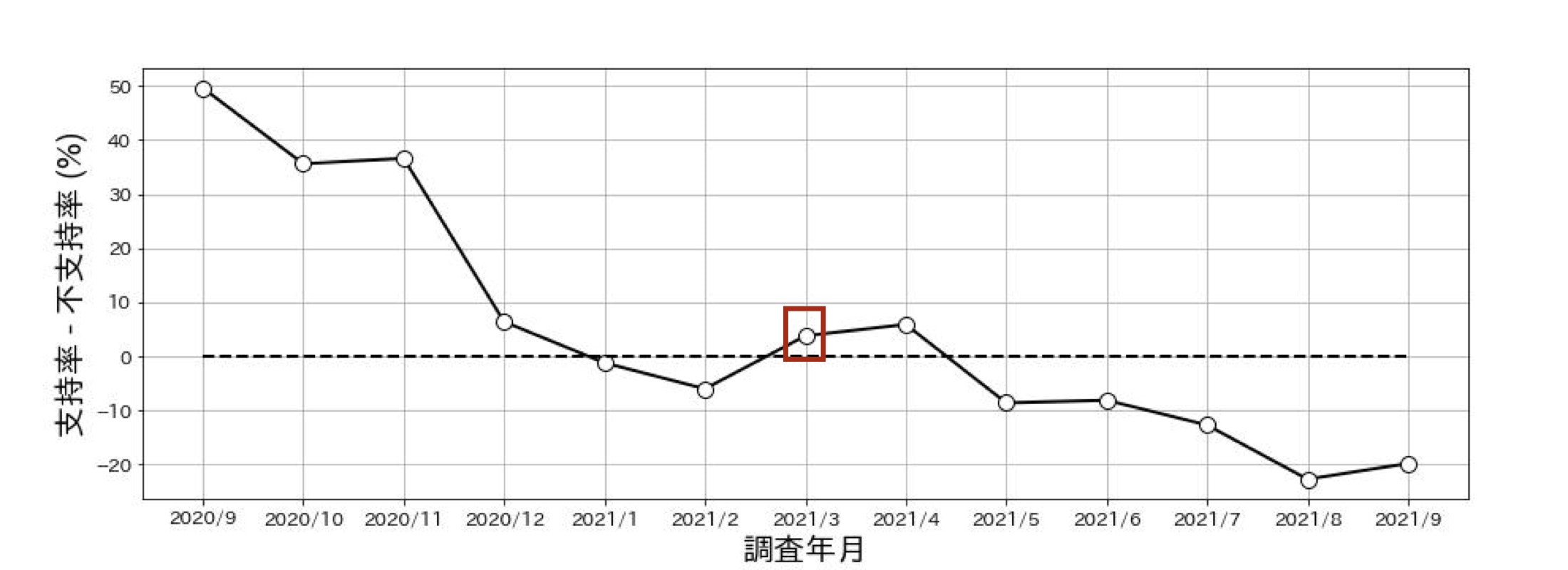
以下の図は、支持率から不支持率を引いたものです。
確かに2021年3月の値は正の領域にいますが、これはどれだけ有意かというのがここでの疑問です。
例えば、差が10%あれば、「なるほど支持が不支持を上回っているのだな」と受け取り、逆に1%だと「いやいや誤差でしょう」と受け取るのが自然かと思いますが、その境界はどこにあるのか気になったので、以下で検証してみました。
今回のアンケート結果が従う分布関数
NHK公式サイトを参照すると、内閣支持率を問う質問には、以下の3つの選択肢から回答することになっているようです。(詳しくはこちら)
1.支持する
2.支持しない
3.わからない、無回答
よって、それぞれの選択肢を選ぶ確率を$p_{1}, p_{2}, p_{3}\ (p_{i}{\geq}0\ (i=1, 2, 3);\ p_{1}+p_{2}+p_{3}=1$)としましょう。
また、有効回答数を$n$と置きます。
さらに、それぞれの選択肢の回答数を$x_{1}, x_{2}, x_{3}\ (x_{i}{\geq}0\ (i=1, 2, 3);\ x_{1}+x_{2}+x_{3}=n$)とします。
$x_{1}, x_{2}, x_{3}$の実現値を取る確率変数$X_{1}, X_{2}, X_{3}$は、$n$と$p_{i}\ (i=1, 2, 3)$をパラメータとする多項分布に従い、その関数形は以下で与えられます。
f(X_{1}=x_{1}, X_{2}=x_{2}, X_{3}=x_{3}; n, p_{1}, p_{2}, p_{3}) = \frac{n!}{x_{1}!x_{2}!x_{3}!}p_{1}^{x_{1}}p_{2}^{x_{2}}p_{3}^{x_{3}}
多項分布の分散、共分散
具体的な導出は専門書に譲るとして、多項分布の分散と共分散を天下り的に以下で与えます。
分散
V(X_{i}) = np_{i}(1-p_{i})
こちらは二項分布でお馴染みの形ですね。
(ただし、今回のケースでは$1-p_{i}$が$p_{i}$でない二つの確率を合算した値を表すので解釈に注意が必要です。)
共分散
Cov(X_{i}, X_{j}) = -np_{i}p_{j}\ (i{\neq}j)
支持を選ぶ人が増えると不支持を選ぶ人が減る(もちろん逆も然り)ので、確率変数間の共分散が常に負となるのは直感にも合います。
支持率・不支持率の差の検定
さて、今興味があるのは、「支持率ないし不支持率がそれ単体で大きいか小さいか」ではなく、「支持率と不支持率の差 $(p_{1}-p_{2})$が、統計的にどれだけ有意か」です。
つまり、$p_{1}-p_{2}$という統計量の標準偏差を求める必要があり、それは以下のような形になります。
\begin{align}
\sqrt{V(p_{i} - p_{j})} &= \sqrt{V\biggl(\frac{X_{i}}{n} - \frac{X_{j}}{n}\biggr)} \\
&= \frac{\sqrt{V(X_{i}) + V(X_{j}) - 2Cov(X_{i}, X_{j})}}{n} \\
&= \frac{\sqrt{p_{1}(1-p_{1})+p_{2}(1-p_{2})+2p_{1}p_{2}}}{\sqrt{n}}
\end{align}
いま、帰無仮説$H_{0}$と対立仮説$H_{1}$を
H_{0}:p_{1} - p_{2} = 0 \\
H_{1}:p_{1} - p_{2} > 0
と設定すると、帰無仮説$H_{0}$の元で、統計量
\frac{p_{1}-p_{2}}{\sqrt{V(p_{i} - p_{j})}}
は標準正規分布に従います。
有意水準5%で片側検定を試みると、
\frac{p_{1}-p_{2}}{\sqrt{V(p_{i} - p_{j})}} > 1.645
の時にこの差は有意と判断されます。
実際に計算すると、
\frac{0.403-0.365}{\sqrt{0.403(1-0.403)+0.365(1-0.365)+2*0.403*0.365}/\sqrt{1237}} = 1.526
となり、1.645より小さくなります。
つまり、2021年3月のNHK世論調査では、内閣支持率が不支持率を上回った結果が有意水準5%では有意とは言えないということがわかりました。
以下は、上に載せた支持率-不支持率のグラフに、ここで計算した95%信頼区間を加えたものです。
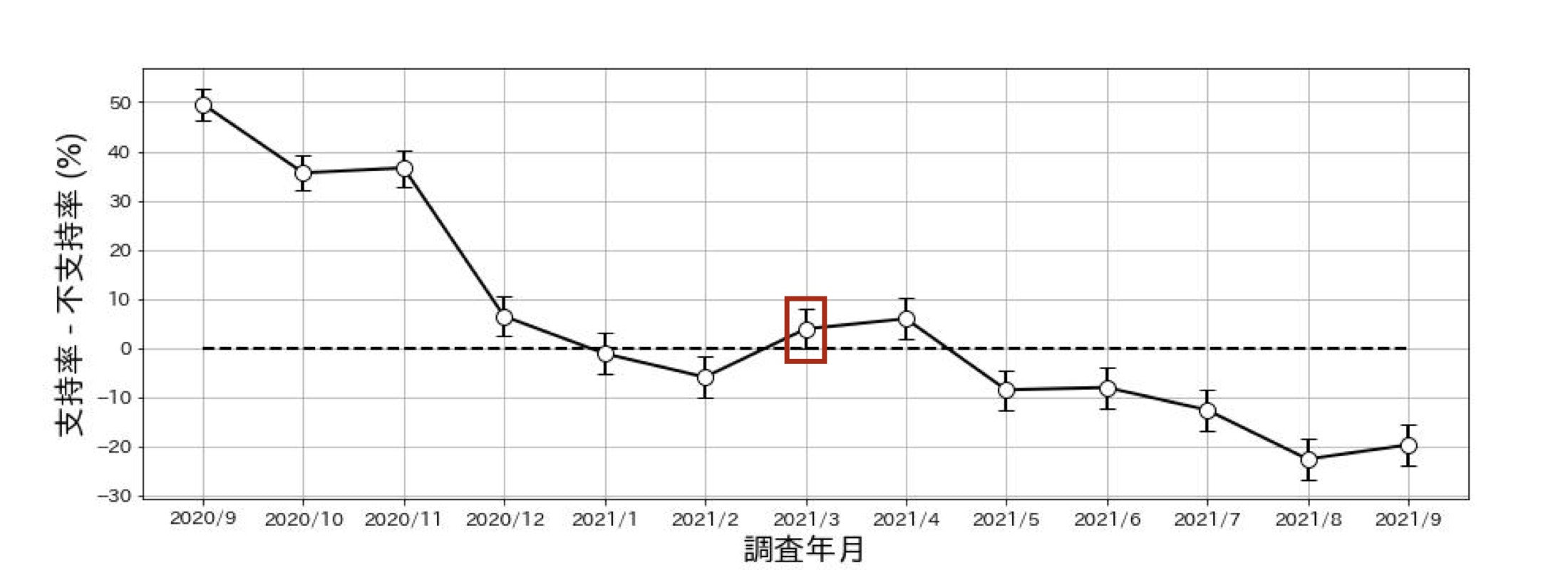
見にくいので、2021年3月周辺を拡大すると、以下のようになります。
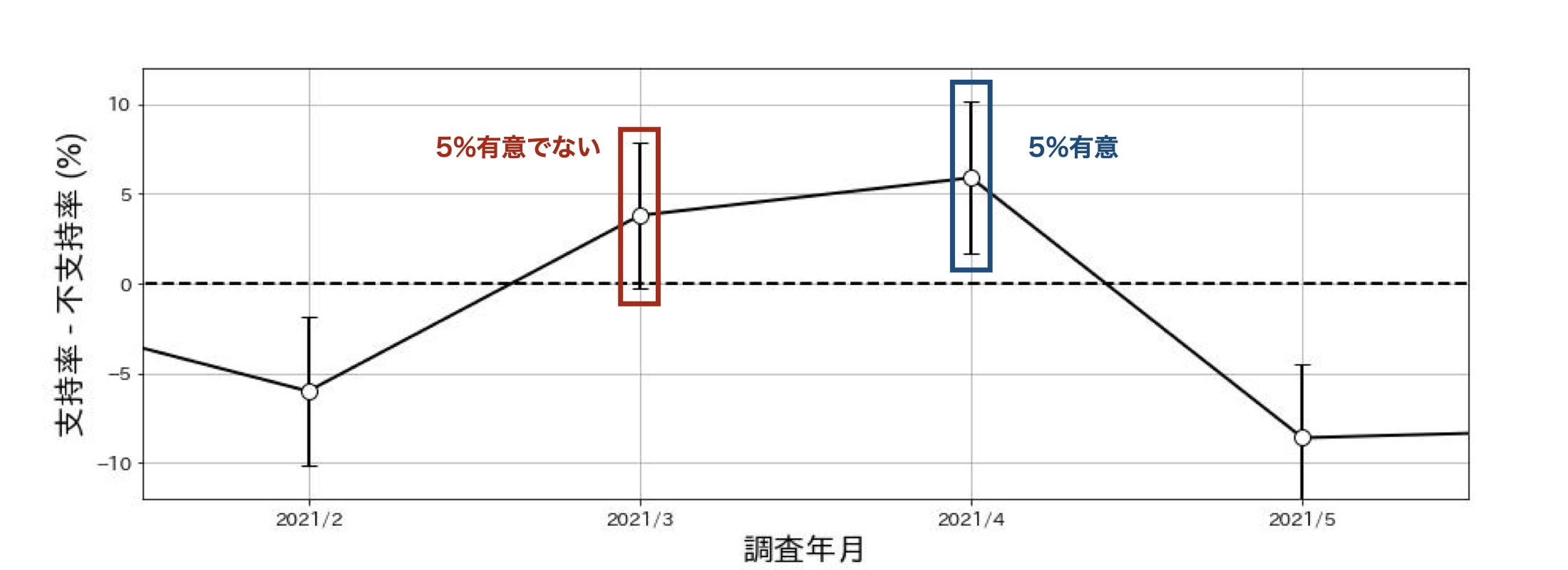
2021年3月の点は95%信頼区間に0が含まれますが、これは有意水準5%では差が有意でないことを意味します。
まとめ
2021年3月のNHK世論調査では、40.3%と36.5%という数字だけを見ると確かに40.3%の方が大きいが、前者が後者と同程度であるという仮説は有意水準5%では棄却されません。
つまり、内閣支持率が不支持率を上回った結果が有意とは言えないということがわかりました。
厳密な言い方をすると、「支持率と不支持率に真に差がない場合でも、今回使ったサンプルにたまたま偏りが存在し、両者に差があると判断される可能性が無視できない」という解釈になります。
余談ですが、上の図に青で示した通り、本当に支持が上回ったと主張するには、翌月(支持44%、不支持38%、有効回答数1222)の結果を待たねばならなかったようです。
おわりに
ちなみに、(上の式から明らかなように)有効回答数$n$を大きくするほど信頼区間の幅は小さくなります。
支持率-不支持率の差を5%有意にするにはどの程度のサンプル数が必要だったのでしょうか。
例えば有効回答数を$n=2000$とすると、
\frac{0.403-0.365}{\sqrt{0.403(1-0.403)+0.365(1-0.365)+2*0.403*0.365}/\sqrt{2000}} = 1.941 > 1.645
となり、2021年3月の支持と不支持の差は5%有意となることがわかります。
昔、「トリビアの泉」というテレビ番組で、一定数の日本人に対するアンケート調査が(割と頻繁に)行われており、毎回ナレーターが「一体何人に聞けば統計的に正しい結果が得られるのか?専門家に聞いてみた。」と発問するコーナーがありました。
その度に統計の専門家枠で毎回必ず同じ学者の方が登場し、毎回必ず「2000人程度に聞くのがよいでしょう」と回答する、という(シュールな)シーンがあったのですが、こういう原理が背景にあったのですね。