はじめに
前回の記事(こちら)で、Hartree Fock法で、対象とする分子の波動関数とエネルギーを得られるようになった。
しかしながら、実際に分子を対象とした電子状態計算を行う際は、一点計算のみを行うことはあまりなく、まずは構造最適化を行い、得られた最適化構造に対して、分子軌道(Molecular Orbital)の可視化や、各種物性値(NMRの化学シフト, IRのピークなど)を求めることがほとんどである。
そこで今回は、前回作成したHartree Fockプログラムを利用して分子のエネルギー勾配を求め、構造最適化っぽいことをする関数を作ってみる。
今回のコードも、例によってここのリポジトリに置いてある。今回は、step3のディレクトリの中にある。
力の定数を求める関数の実装
「力の定数」と聞いた途端に、現在主流の解析解の存在を思い浮かべる方もいらっしゃるかもしれない。しかし、ここではそんな凄いことはせず、中間差分法を用いることにする。
中間差分法における微分係数は、
\frac{dF(x)}{dx} = \frac{F(x+h) - F(x-h)}{2h}
により求められる。
これにしたがって、それぞれの原子核をxyz方向に少しだけ動かし、エネルギーの勾配を得るという極めて原始的な方法をとる。コードは以下のような感じになる。
def perturbate_system(atom, index, displacement):
ret = []
for i in range(len(atom)):
if i != index:
ret.append( atom[i] )
else:
ret.append( Nuclear(atom[i].pos + displacement, atom[i].atomic_number) )
return ret
def grad(nelec, basis_functions, atom, dr = 0.05):
if dr < 0: raise
ret = []
for i in range(len(atom)):
system = perturbate_system(atom, i, np.array([+dr, 0, 0]))
basis = generate_basisfunctions(system, basis_functions)
pdx = rhf(nelec, basis, system)
del system, basis
system = perturbate_system(atom, i, np.array([-dr, 0, 0]))
basis = generate_basisfunctions(system, basis_functions)
mdx = rhf(nelec, basis, system)
del system, basis
system = perturbate_system(atom, i, np.array([0, +dr, 0]))
basis = generate_basisfunctions(system, basis_functions)
pdy = rhf(nelec, basis, system)
del system, basis
system = perturbate_system(atom, i, np.array([0, -dr, 0]))
basis = generate_basisfunctions(system, basis_functions)
mdy = rhf(nelec, basis, system)
del system, basis
system = perturbate_system(atom, i, np.array([0, 0, +dr]))
basis = generate_basisfunctions(system, basis_functions)
pdz = rhf(nelec, basis, system)
del system, basis
system = perturbate_system(atom, i, np.array([0, 0, -dr]))
basis = generate_basisfunctions(system, basis_functions)
mdz = rhf(nelec, basis, system)
del system, basis
dEdx = (pdx-mdx)/(2*dr)
dEdy = (pdy-mdy)/(2*dr)
dEdz = (pdz-mdz)/(2*dr)
ret.append( np.array([dEdx, dEdy, dEdz]) )
return ret
perturbate_system()という関数で、指定したインデックスの原子を少しだけ動かした新しい分子座標を作るようにしている。
その分子座標を使って、エネルギー計算を行い、最後にまとめて差分方による微分係数を求める。
構造最適化の関数の実装
構造最適化において現在主流なのはZマトリックスなり、Redundantのような内部座標を用いて、共役勾配法やNewton Raphson法などで最適化構造を探していくようだが、ヘシアンを作ったりするのも面倒なので今回は最急降下法で書いてみた。
おさらいになるが、最急降下法のアルゴリズムは、
(数式はwikipediaより引用)
要するに勾配の一番大きな方向に動かすのみである。上述したグラジエント関数によって、dE/dRが得られているので、これを小さくする方向、つまりグラジエントに対して負のスケールファクターを乗じた方向に向かって原子を動かしていけば良い。こちらのコードは下記。
def update_system(atom, force, scale):
# Tiny Steepest Descent Algorithm
new_system = []
for i in range(len(atom)):
displacement = -1.0 * scale * force[i]
new_system.append( Nuclear(atom[i].pos + displacement, atom[i].atomic_number) )
return new_system
最後に、ここまで述べた関数の呼び出し元であるoptimize関数を以下に示しておく。なお、構造最適化の収斂条件は適当で、一つ前のステップの時と比べてエネルギーの差が閾値以下になったら終わったことにしている。普通は、各原子の変異と力の大きさのRMSDと最大値の全てが閾値以下になったら終わったことにするはず。
def optimize(nelec, basis_functions, atom, max_step = 10, dr_for_grad = 0.05, scale_for_displacement = 0.8, converge_criteria = 0.0001):
system = atom
energy_history = []
optimized_flag = False
for n_step in range(max_step):
print("Optimization step:{}".format(n_step))
for i in range(len(system)):
print("{} {}".format(system[i].atomic_number, system[i].pos))
bfs = generate_basisfunctions(system, basis_functions)
energy_history.append( rhf(nelec, bfs, system) )
if 1 <= n_step and abs(energy_history[-1]-energy_history[-2]) < converge_criteria:
optimized_flag = True
break
force = grad(nelec, basis_functions, system, dr_for_grad)
system = update_system(system, force, scale_for_displacement)
if optimized_flag == True:
print("Optimize Done")
print("Energies: ", energy_history)
else:
print("Optimized Failed")
return (optimized_flag, system)
動作テスト
とりあえず、上記のプログラムを使って、水素分子H2について、核間距離2.0(a.u.)から初めて、1.4(a.u.)くらいのところに収束するかどうか試してみる。最急降下法でのスケールファクターは-0.8にしておいた。
構造最適化のステップごとの核間距離とトータルエネルギーの値は、以下の通り。2.0から始めているので、グラフの線の右から左に向かって構造最適化が進んでいることになる。
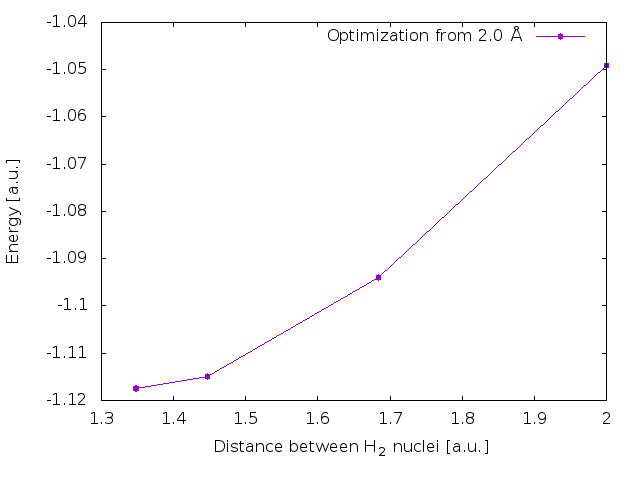
結果として、1.36[a.u.]程度の核間距離に収束しており、まぁいい線行っているのではないだろうか。
GaussianやGAMESSなどを使ってみんなが興味深いと思うような分子を扱おうとすると、こんなのでは1ミリも喜べないのだがw、趣味で作った自作のプログラムがそれっぽく動いてくれるのはやっぱりうれしい。そしてパッケージプログラムの有り難みがよくわかる。
最後に
「構造最適化っぽい」ことが一応行えるようになったわけだが、ここで行っている方法は効率の面のみならず、信頼性の観点からも現在一般的になものには足元にも及ばない。しかしながら、上記で取り扱った勾配を求める手法と数値最適化アルゴリズムのそれぞれを良いものにしていくと、現在一般に使われているものに近づけていくことができる。これについて少しだけ言及しておく。
まず、微分について。微分は、この記事では、それぞれの原子核を正負のxyz方向に微小距離だけ動かして一点計算を行い、差分法で求めた。これだと、計算の回数は6N(Nは原子数)となってしまい、あまりに効率が悪い1。現在一般的なのは、SCFにより得られた波動関数から、解析的に微分係数を求める方法である。これにより、一度SCFを収束させるだけで、あとは機械的に力の大きさを求めることができる(ただし、式は複雑)。詳しくは、Pulayの論文(参考文献2)を参照。
次に、最適化のアルゴリズムについて。最適化には勾配の情報の他に、「そもそも何を変数とするか」が重要な要素である。原子のデカルト座標をそのまま最適化の変数にするのはあまり賢い方法ではなく、現在の(というかかなり昔から?)Gaussianでは、結合距離や結合角、二面角といった変数をもとに内部座標を作成するようになっている。
また、最適化アルゴリズムについては、ここで用いた再急降下法は平衡構造あたりでの収斂に問題がある。そのほかにも問題や最適化の程度に応じて適当なスケールファクターを選ぶ術がないということも問題である。
これに変わって、現在は(いや、多分これもかなり前から)準ニュートン法などを用いるのが主流である。準ニュートン法は、二階微分係数(変数が複数ある場合は、ヘシアン)が必要となってくるが、そのおかげで最適化構造から遠く離れた場所では、変位を大きく、最適化構造に近づいてきたら微小な変位をとることができる(詳しくはWikipedia参照)。二階微分の計算には解析解ももちろん存在するが計算コストが大きいので、一般的には、解析的に得られた1階微分をつかって差分法で求めていくようである。
ここまでいろいろ述べてきたが、私は計算化学エンジョイ勢(パッケージソフトのユーザー側であって考える側ではない)なので、日々これらの改善に注力されている方に見られたらボコボコにされそうで怖い。頭が上がりません。ただ、認識として間違っている部分があるかもしれないので、ここは一つマサカリの方宜しくお願いします。
参考文献
- Gaussian 16 Users Reference (http://gaussian.com/man/)
- Pulay, Peter. "Ab initio calculation of force constants and equilibrium geometries in polyatomic molecules: I. Theory." Molecular Physics 17.2 (1969): 197-204.
- 金谷 健一 「これなら分かる最適化数学―基礎原理から計算手法まで」 共立出版
今回の参考文献はあまり思いつかないのだが(自明なことしか書いてないので)、まずはGaussianのマニュアルだろうか。Gaussianの中で使われている最適化アルゴリズム(Berny Optimizationとかいうやつ)は私はよくわかっていない。
2番目は、上記でも述べたPulayの有名な文献である。2017年11月30日の時点で、引用数2469という、非常に重要な論文である。
3番目の教科書は、最適化数学の入門としていい本だと思う。
-
Gaussian09までは、TDDFTでの振動計算の時はこの方式の微分を使っていたが、Gaussian16でこれも解析微分できるようになった。 ↩
