歩きスマホの警告をシミュレーションでやってみた！

#はじめに
この記事は明治大学Advent Calendar 2018の18日目の記事です。はじめての投稿で、拙い文と内容だと思いますが、少しでも楽しんで読んでいただけたら幸いです！

#目的
歩行者のパーソナルスペースと人数に対する衝突回数の変化を考察する。

〜注意〜
**・**本記事で使われているプログラムはProcessingで書かれています。
**・**あくまで個人的な見解であり、他にもいい方法はたくさんあると思います。

#単純な歩行者の作成
##イメージ
今回作成する歩行者は、2次元平面上の移動を考えます。
移動は、自分の位置$(x,y)$と目的地 $(p,q)$ とを結ぶ直線、つまり自分と目的地までの距離を最も早く短くできる方向に進むものだと考えます。
##数学的な移動方法
手法は最急降下法を用いました。

詳しくない方に、最急降下法の簡単なイメージだけ伝えると、
「ある山の中腹にいた時に、あなたは360度どの方向でも進むことができます。でも、一番早く山の下の宿舎に下りていくための方向は、宿舎への距離を縮めてくれる最も大きな変化量がある方向に決まりますよね。
といった感じ。

真面目に話すと、最急降下法は勾配法とも言い、$x$ 方向の勾配と　$y$ 方向の勾配を計算し、次の自分の座標を更新していく手法です。
自分の位置を$(x,y)$ とし、目的地の座標を$(p,q)$ とすると、
２点間の距離は、$$f(x,y)=\sqrt{(x-p)^2+(y-q)^2}$$と表せますね。
手法通り、 $x$ の勾配を求めるために $x$ について $f(x,y)$ を偏微分すると、

\begin{eqnarray*}

\frac{\partial f}{\partial x}&=&\frac{\partial}{\partial x}\left({(x-p)^2+(y-q)^2}\right)^{\frac{1}{2}}\\
&=&\frac{1}{2}\frac{2(x-p)}{\sqrt{(x-p)^2+(y-q)^2}}\\
&=&\frac{(x-p)}{\sqrt{(x-p)^2+(y-q)^2}}

\end{eqnarray*}

上のような式を得られます。
$y$ についても同じく、

\frac{\partial f}{\partial y}=\frac{(y-q)}{\sqrt{(x-p)^2+(y-q)^2}}

を得ることができます。

ここで、ある時刻 t における自分の座標を$(x_{t},y_{t})$として、時刻 t+1 の時の座標を上記の式を用いて表すと、

\begin{eqnarray*}

(x_{t+1},y_{t+1})&=&(x_{t},y_{t})-\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)\\
&=&(x_{t},y_{t})-\left(\frac{(x_{t}-p)}{\sqrt{(x_{t}-p)^2+(y_{t}-q)^2}},\frac{(y_{t}-q)}{\sqrt{(x_{t}-p)^2+(y_{t}-q)^2}}\right)

\end{eqnarray*}

となり、これを繰り返すことで目的地まで向かっていきます。

##プログラムとシミュレーション
さて、実際にランダムに自分の初期位置と目的地を決定して、目的地に向かっていく様子を見てみましょう！
まず $500\times500$ の2次平面上に、ある一人の人物の初期位置と目的地をランダムにセットします。

//人数の設定
int humanN = 1;

//自分の位置と目的地のベクトル行列
PVector pedestrian[] = new PVector [humanN];
PVector destination[] = new PVector [humanN];


void setup(){
　//平面の作成
  background(255);
  size(500,500);
  
　//初期化
  for(int i=0; i<humanN; i++){
    pedestrian[i] = new PVector();
    destination[i] = new PVector();
  }
  
　//初期値の設定
  for(int i=0; i<humanN; i++){
    pedestrian[i].set(random(0,500),random(0,500));
    destination[i].set(random(0,500),random(0,500));
  }
}

セットしたら、目的地に向かって動かしましょう！
この時、ゴールとの距離が１未満になったら新しくフィールドに生まれ変わるよう条件をつけると...

//距離保存用の箱
float p_dDistance;

//各歩行者の距離の更新 (最急降下法)
for (int i=0; i<humanN; i++) {
  p_dDistance=dist(
    pedestrian[i].x, pedestrian[i].y, destination[i].x, destination[i].y
  );

  if (p_dDistance>=1) {
      pedestrian[i].set(
        pedestrian[i].x-(pedestrian[i].x-destination[i].x)/ p_dDistance, 
        pedestrian[i].y-(pedestrian[i].y-destination[i].y)/ p_dDistance
      );
    } else {
      pedestrian[i].set(random(0, 500), random(0, 500));
      destination[i].set(random(0, 500), random(0, 500));
    }
  }

このように書くことができ、描画すると

こんな感じ！

#すれ違ったりスマホを持ったりする歩行者の作成
##歩行者同士のすれ違い
今作成した歩行者同士をすれ違わせてみましょう！
実装したいイメージは、
「ある範囲に入ってきた人から最も離れる方向に進もう！」
となります。
聞き覚えのある言い回しだとお気付きの方もいるでしょう。
ここでも最急降下法を使って表現していきます。
ある歩行者 $i$ がいて、ある時刻 $t$ での座標を $(x^i_t,y^i_{t})$ 、目的地の座標を $(p^i,q^i)$ とする。この時、ある歩行者 $k$ が歩行者 $i$ の避けたい範囲に入った場合の計算は以下のようになります。

\begin{eqnarray*}

(x_{t+1}^i,y_{t+1}^i)=(x_{t}^i,y_{t}^i)&-&\left(\frac{\partial f}{\partial x_t^i},\frac{\partial f}{\partial y_{t}^i}\right)\\
&+&\left(\frac{(x_{t}^i-x_{t}^k)}{\sqrt{(x_{t}^i-x_{t}^k)^2+(y_{t}^i-y_{t}^k)^2}},\frac{(y_{t}^i-y_{t}^k)}{\sqrt{(x_{t}^i-x_{t}^k)^2+(y_{t}^i-y_{t}^k)^2}}\right)

\end{eqnarray*}

上記の単純な歩行者に追加するような式構成になっています。
すれ違いの様子はこんな感じ！

前から来た相手を避けている様子がわかりますね！
##スマホを持たせるには？
すれ違いができる歩行者を作成した時に、「ある範囲に入った相手を避ける」という条件を設定していましたよね？この条件は、人間の視野やパーソナルススペースをイメージしたもので、スマホを持っている = 視野が狭いという考えから、避けようとする範囲が極端に狭い歩行者を作ればいいことになります。
ここから、シミュレーションでは次の２パターンを考えましょう！
歩行者同士の距離を $Distance$ として、歩行者のサイズを8だとすると、

 \begin{cases}
     スマホなし：1\le Distance \leq16\\
\\
    スマホあり：1\le Distance \leq9
  \end{cases}

このように避ける範囲の区別をすることができ、スマホなしは自分の1.5倍先を視野に、スマホありは自分の目の前を視野にしていることが表現できている。
##シミュレーション
上記で説明した人を避ける条件と歩きスマホか否かの条件を単純な歩行者のプログラムに足して、歩行者天国 渋谷のスクランブル交差点のシミュレーションを見てみましょう！
人数は100人、そのうち歩きスマホの割合が2割のときのシミュレーションで、5つの方向から歩行者が流れてきます。
右上の $count$ が衝突回数、$time$ がステップ数を表しています。

誤解のないように幾つか条件を説明すると、
・衝突は歩行者を模した丸同士が接触した時に加算され、連続で衝突したものは数えない。
・歩行者はステップ数が0~1200で歩行し、1201~2000で信号待ちを行う。
・信号待ちの間は衝突をカウントしない。
大まかにこのようになっています。

#衝突回数の考察
歩行者数100名のときの、スマホ持ちの割合と衝突回数の推移はこのようになりました。
それぞれの割合の時のシミュレーション結果100回分の平均をとり、プロットしています。

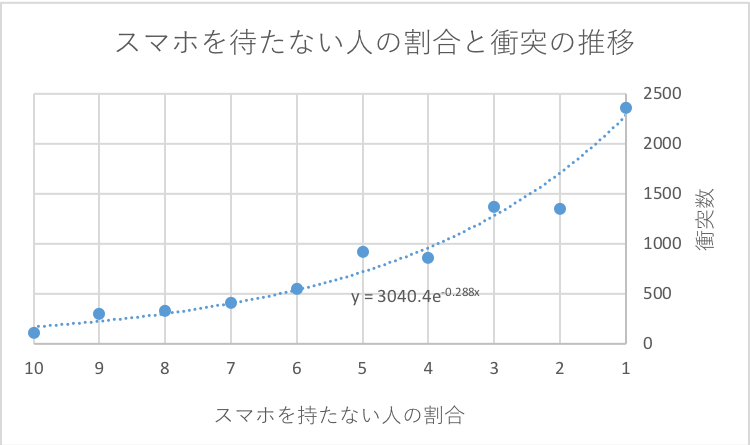
割合が増えるにつれ、指数関数的に衝突回数が上昇していることがわかると思います。
歩行者の数を200人や300人にした場合でも同じような増加をしていました。
このことから、歩きスマホによって視野が狭くなると人との衝突を引き起こしやすく、その割合が高いほど危険であると言えます。

#まとめ
さて、シミュレーションの結果から歩きスマホが衝突の回数を上げる要因になりうることがわかりました！常にフィールドに一定人数がいる点では現実と異なっていますが、歩きスマホの危険性は伝わったのではないでしょうか？
今回のシミュレーションで重要なのは最急降下法の理解のみです！プログラムの基礎知識があれば誰でも歩行者は描けると思います。

今回の記事の根本は、
「疑問とアイデアをどうプログラムに反映していくのか、どんな数学の知識が生きていくのか！そんなワクワクを多くの人と共有したい！」
という思いです。
現実の現象に疑問を持って多くの人と語らう、そんなことを皆さんもこれを機にしていただければ幸いです！