動かして理解するレーティングシステム

これはAteam LifeDesign Advent Calendar 2022の1日目です。

さて本日2022年12月1日は何の日でしょうか？そうです、スプラトゥーン3のXマッチの解禁日¹であり、ポケットモンスタースカーレット・バイオレットのランクマッチ解禁日²です。

このような対戦型ゲームには、プレイヤーの相対的な強さを表す レーティング の仕組みが用意されています。対戦型ゲームをプレイしていると、「1500」ぐらいを初期値として始まって、勝てば勝つほど増えていって、強い人ほど高い数値になるようなものを見たことがあるのではないかと思います。あの数値のことです。

本稿ではこの「レーティング」の数値の計算の仕組みとして、一般に公開されているものをいくつか紹介し、簡単なPythonプログラムで実際に動かしてみることで挙動を調べていきます。
スプラトゥーンのようなコンピュータゲームはもちろん、チェスや将棋などのアナログ対戦ゲームや、サッカー等の対戦スポーツにおいてもレーティングは使われています。ですので、馴染みのあるゲームを思い浮かべていただくとイメージしやすいと思います。

用語の定義

スプラトゥーン3では「Xパワー」と呼ばれるように、ゲームによって数値の呼称に差がありますが、本稿ではすべて「レーティング」と呼びます。また、プレイヤーが1回ゲームをして勝敗が決まりレーティングが変化すること³を「試合」と呼びます。

環境

• Google Colaboratory
  • Python 3.7.15
  • bokeh: 2.3.3

本稿では3つの手法を比較しますが、比較時のインターフェースの統一性のために3つのレーティングシステムについて同一の開発者による以下の実装を利用します。これらはすべて似たようなメソッド名によるインターフェースを持っています。

• sublee/elo: An implementation of the Elo rating system for Python
• sublee/glicko2: An implementation of the Glicko-2 rating system for Python
• sublee/trueskill: An implementation of the TrueSkill rating system for Python

ただし、sublee/glicko2については現状メンテナンスされておらず、依存関係の問題でpip installによる導入ができません。本稿では以下のように単体のプログラムファイルをGitHubから直接取得して動作させます。

!wget https://raw.githubusercontent.com/sublee/glicko2/master/glicko2.py

import glicko2
player_a, player_b = glicko2.Rating(1400), glicko2.Rating(1000)

実際にGlicko Ratingを使いたい場合は、別のライブラリの利用や自前での実装を検討してください。

相対的な強さ

本稿で取り扱うレーティングシステムの動機は、「ふたりのプレイヤーがあるゲームをした時に、どちらが強いかを決めたい」ということです。

ふたりのプレイヤーのどちらが強いかを決めるには、直接対決をした結果を用いるのがもっともシンプルです。
「プレイヤーAとプレイヤーBが試合をして、Aが勝った」ならば「AはBよりも強い」ということです。簡単ですね。

この「強さ」の定義は当たり前のように見えますが、完璧なものでしょうか？
たとえば、じゃんけんの手を思い浮かべて下さい。グーとパーが10回戦ったらパーが10回勝ちます。だから「グーは弱い・パーは強い」と言えるでしょうか。当然、じゃんけんにおいては「グー」「チョキ」「パー」の3種類の手があって、すべての手が平等に出てくる環境においては、勝つ確率（勝率）はグーもパーも33%です。どちらが強いとかはありません。むしろ、何らかの理由でチョキが多い環境であれば、グーの勝率はパーよりも高くなります。

直接対決の結果は、他の指標において互角の強さで強弱が付かなかった時に最後の決め手として使われる事はありますが、それだけが絶対的な指標ではありません。

勝率

さて、先程の例において 勝率 が出てきました。勝率も、プレイヤーの相対的な強さを表す上でシンプルな手法のひとつです。説明するまでもないかもしれませんが、勝率とは、勝った回数を試合の回数で割ったもので、勝率は0以上1以下のあいだの値を取ります。

勝率が高いほど強いプレイヤーと言えるでしょうか？対戦相手がランダムだったりして条件が全く同じならば、そう言えると思います。
しかし、

• プレイヤーAは、弱い相手ばかりと戦い続けていて、勝率が60%
• プレイヤーBは、強い相手ばかりと戦い続けていて、勝率が50%

この場合「勝率60%のプレイヤーの方が、勝率50%のプレイヤーよりも強い」とは言えるでしょうか。Bはどれぐらい強い相手と戦ったのか？といった、対戦相手の強さなどの情報が無いと、勝率だけで誰が強いかは判断できません。
勝率だけが唯一の指標である場合、意図的に自分よりも弱い相手とばかり戦い続けることで勝率を高い値に保つようなことができてしまうかもしれません。それは強いプレイヤーと言えるでしょうか。

特に最近のコンピュータゲームなどでは、なるべく同じ実力の人同士がマッチングするようになっています。自分よりも明らかに弱いプレイヤーや強すぎるプレイヤーとの試合が組まれにくいように、様々な工夫がされています。
そのため、強い人でも強い人ばかりと試合をした結果勝率が50%を下回ったり、逆に弱い人でも勝率が50%を超えるような事も、珍しくありません。

このように、勝率だけでプレイヤーの強さを表す事はできません。

Elo Rating

ここから レーティング の話をしていきます。イロ・レーティング（Elo Rating）は、以下のような特徴を持ちます。

• 強い人ほど大きな値になりやすい
• 試合をすると両者のレーティングが更新され、勝ったら上がり、負けたら下がる
• レーティングが高い人（強い人）と戦って勝つほど、大きく変動する

細かい話をする前に、試しに動かしてみましょう。
!pip install eloでsublee/eloをインストールして、以下のプログラムを動かしてみます。

import elo

player_a, player_b = elo.Rating(1400), elo.Rating(1000)
print(f'プレイヤーA: {float(player_a):.0f}, プレイヤーB: {float(player_b):.0f}')

# 第一引数に勝者、第二引数に敗者。（プレイヤーAの勝ち）
player_a, player_b = elo.rate_1vs1(player_a, player_b)

print(f'プレイヤーA: {float(player_a):.0f}, プレイヤーB: {float(player_b):.0f}')

出力

プレイヤーA: 1400, プレイヤーB: 1000
プレイヤーA: 1401, プレイヤーB: 999

レーティングが1400のプレイヤーAと、1000のプレイヤーBの2人がいるとします。2人が試合をして、プレイヤーAが勝ったとします。
このとき、プレイヤーAのレーティングは1400→1401と、1だけ増加しました。同様にプレイヤーBのレーティングは1000→999と1減少です。レーティングの変動は1でした。

では逆に、番狂わせが起きてレーティング1000のプレイヤーBが勝ったとします。

player_a, player_b = elo.Rating(1400), elo.Rating(1000)
print(f'プレイヤーA: {float(player_a):.0f}, プレイヤーB: {float(player_b):.0f}')

player_b, player_a = elo.rate_1vs1(player_b, player_a)

print(f'プレイヤーA: {float(player_a):.0f}, プレイヤーB: {float(player_b):.0f}')

出力

プレイヤーA: 1400, プレイヤーB: 1000
プレイヤーA: 1391, プレイヤーB: 1009

今度は、プレイヤーAのレーティングは9減少、プレイヤーBのレーティングは9増加しました。このようにレーティングの高い相手に勝つと、大きく変動します。

最初は全員レーティング1500などの一定値からスタートします。試合を繰り返していくと、より強い人ほどレーティングが高く、弱い人ほどレーティングが低くなっていきます。十分に試合回数を積めば、レーティングの高さが強さを表すようになる、というアイデアです。
強い人はより強い人と試合をしないとレーティングが上がりにくくなっています。先程の「弱い人とばかり試合をしていて勝率が高い」人は、レーティングが上がりにくいようになっています。

レーティングの数値の意味を、もう少し見てみます。レーティングの差は、勝率の予測値を表すようになっています。相手よりもレーティングが高ければ高いほど勝率が高くなります。つまり、ふたりのプレイヤーのレーティングの差は 相対評価 を表していると言えます。

たとえば、レーティングに400差があるプレイヤー同士の対戦は、弱いプレイヤーが勝つ確率よりも強いプレイヤーが勝つ確率の方が10倍高くなるようになっています。
勝率は以下のプログラムで求められます。

def elo_win_probability(r1, r2):
    x = (r1 - r2) / 400           #...式1
    return 1 / (1 + 10 ** (-x))   #...式2

elo_win_probability(1000, 1400)

出力

0.09090909090909091

勝率は約9%でした。この値を11倍すると1.0となり、1400のプレイヤーが勝つ確率は1000のプレイヤーの10倍であることが確認できます。

さて、この勝率を計算した式は一体何でしょうか。式1のx = (r1 - r2) / 400はレーティングの差を400で割ったものです。つまり、レーティング差が400あるとちょうど1になります。
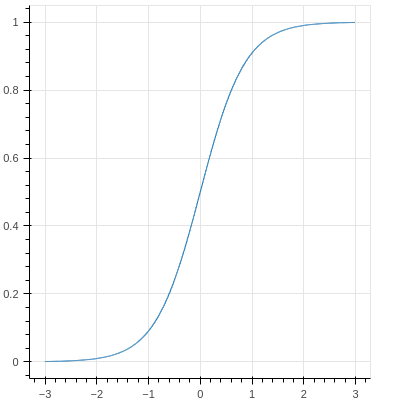
式2のreturn 1 / (1 + 10 ** (-x))はいわゆるロジスティック関数ですが、Bokehでグラフを書いてどんなものか確認してみましょう。

from bokeh.io import output_notebook, show
from bokeh.plotting import figure 
output_notebook()

xs = [ x / 100 for x in range(-300, 300, 1) ]
ys = [1 / (1 + 10 ** (-x)) for x in xs]

p = figure(plot_width=400, plot_height=400)
p.line(x=xs, y=ys)
show(p)

x軸はレーティングの差（を400で割ったもの）です。x=0のときレーティングが一緒の値で、勝率は50%になっていて、レーティング差が付くほど勝率が変化するようになっています。
x=1のときyが0.91ぐらいになっており、レーティング差が400あると勝率91%ぐらいあるということを表しています。レーティング差が大きければ大きいほど、勝率は1に近づくようになっています。

このように、レーティングの差は予想される勝率を表すようになっています。
たとえばレート1500のプレイヤーが

• レート1900のプレイヤーに勝つ確率は、約9%
• レート1500のプレイヤーに勝つ確率は、50％
• レート1100のプレイヤーに勝つ確率は、約91%

のようになります。
そして勝敗によってレートが増減することで、適正な勝率を表す数値へとレーティングが収束していくようになっています。

簡易版Elo Rating

Elo Ratingは対数計算を含んでおり、ちょっと暗算で計算するのは難しかったりします。以下のような計算式でElo Ratingを近似した簡易版が用いられることがあります。

def simple_elo_rate_1vs1(r1, r2):
    x = (r1 - r2) / 400
    return (
        r1 + 10 * (-(x / 2) + 0.5),
        r2 - 10 * (-(x / 2) + 0.5)
    )

print(simple_elo_rate_1vs1(1300, 1000))
print(simple_elo_rate_1vs1(1000, 1300))

出力

(1301.25, 998.75)
(1008.75, 1291.25)

先程のElo Ratingと似たような感じで、レーティング差が高い相手に勝った時ほどレーティングが大きく変動しています。

この簡易版Elo Ratingにおいて、勝率の予測値は以下の計算で求められます。

def simple_elo_win_probability(r1, r2):
    x = (r1 - r2) / 400
    return (x / 2) + 0.5

simple_elo_win_probability(1000, 1300)

出力

0.125

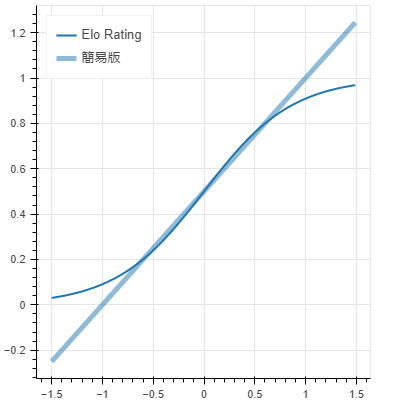
ただの1次関数であり、ずいぶんシンプルな式です。この勝率のグラフを、先程のElo Ratingと重ねてみましょう。

xs = [ x / 100 for x in range(-150, 150, 1) ]
ys = [1 / (1 + 10 ** (-x)) for x in xs]
ys_simple = [(x / 2) + 0.5 for x in xs]

p = figure(plot_width=400, plot_height=400)
p.line(x=xs, y=ys, line_width=2, legend_label="Elo Rating")
p.line(x=xs, y=ys_simple, line_width=5, line_alpha=0.5, legend_label="簡易版")
p.legend.location = "top_left"
show(p)

x=0付近では、グラフは重なっていてほとんど一致していて、近似できていそうです。ですが、x=0.5（レーティング差200）を超えたあたりから乖離していきます。
レーティングの差が大きくない場合なら、この簡易版の計算式はElo Ratingと同じような挙動をします。一方で、レーティングの差が400を超えると勝率の予想値は100%を超えてしまって異常値になっています。レーティングの差が400を超える場合の計算には例外処理が必要になります。

実際に、ポケモンのランクバトルにおけるレート変動は、この簡易版Elo Ratingの計算式が使われているようです。⁴

Glicko Rating

Elo Ratingを改良したのが Glicko Rating（グリコ・レーティング） です。実際にはGlicko Ratingをさらに改良したGlicko-2 Ratingが現在は使われているようです。

Elo Ratingはゲームを始めた時は全員1500などの同じ値からスタートしますが、ゲームを始めたばかりのプレイヤーの強さはよく分かりません。1500と言っても本当はもっと強いかもしれないし、弱いかもしれません。統計の用語を使っていうと、新規プレイヤーのレーティングの 平均 は1500だとしても、 分散 が大きい状態です。

Glicko Ratingにおいては、レーティング偏差という値を導入しました。ゲームを始めたばかりで試合数の少ないプレイヤーや、最後に試合をしてから時間が経っているプレイヤーはレーティング偏差の値が大きくなり、試合をたくさんしたプレイヤーはレーティング偏差の値が小さくなっていきます。

実際にはプレイヤー毎に以下のパラメータが設定され、変動していきます。パラメータの初期値はゲームによって変わることがあります。

名称	初期値	数式上の記号5	説明
レーティング	1500	$\mu$（mu）	強さ
レーティング偏差	350	$\phi$（phi）	強さの振れ幅
レーティング変動値	0.06	$\sigma$（sigma）	強さの変動

レーティング偏差の値は標準偏差（分散の正の平方根）と同じです。説明は省略しますが、グラフで表すとレーティング1500・レーティング偏差350のプレイヤーの実際の強さは下記のような分布になっているということです。

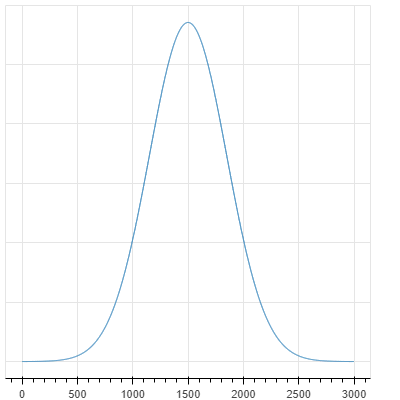
グラフ表示用のコード

import numpy
from scipy.stats import norm

xs = numpy.arange(0, 3000, 1)
ys = norm.pdf(xs, 1500, 350)

p = figure(plot_width=400, plot_height=400, y_axis_location=None)
p.line(xs, ys)

show(p)

実際にsublee/glicko2を使ってみます。Elo Ratingと同じように、レーティング差が400あるプレイヤー同士の勝敗を考えてみます。

import glicko2

player_a, player_b = glicko2.Rating(1400), glicko2.Rating(1000)
print(f'プレイヤーA: mu={player_a.mu:.0f} phi={player_a.phi:.0f}, プレイヤーB: mu={player_b.mu:.0f} phi={player_b.phi:.0f}')

glicko2_rating = glicko2.Glicko2()

# 第一引数に勝者、第二引数に敗者
player_a, player_b = glicko2_rating.rate_1vs1(player_a, player_b)

print(f'プレイヤーA: mu={player_a.mu:.0f} phi={player_a.phi:.0f}, プレイヤーB: mu={player_b.mu:.0f} phi={player_b.phi:.0f}')

プレイヤーA: mu=1400 phi=350, プレイヤーB: mu=1000 phi=350
プレイヤーA: mu=1466 phi=311, プレイヤーB: mu=934 phi=311

レーティング差が400あるプレイヤー同士の試合において、プレイヤーAが勝ったときレーティングが66増えました。また、どちらのプレイヤーもレーティング偏差は等しく311に減っています。

同じ条件でプレイヤーBが勝ったらどうなるでしょうか

import glicko2

player_a, player_b = glicko2.Rating(1400), glicko2.Rating(1000)
print(f'プレイヤーA: mu={player_a.mu:.0f} phi={player_a.phi:.0f}, プレイヤーB: mu={player_b.mu:.0f} phi={player_b.phi:.0f}')

glicko2_rating = glicko2.Glicko2()

# 第一引数に勝者、第二引数に敗者
player_b, player_a = glicko2_rating.rate_1vs1(player_b, player_a)

print(f'プレイヤーA: mu={player_a.mu:.0f} phi={player_a.phi:.0f}, プレイヤーB: mu={player_b.mu:.0f} phi={player_b.phi:.0f}')

プレイヤーA: mu=1400 phi=350, プレイヤーB: mu=1000 phi=350
プレイヤーA: mu=1092 phi=311, プレイヤーB: mu=1308 phi=311

1400→1092と、308も大きく減少しました。

では、同じくレーティング差が400ある試合でプレイヤーBが勝った場合で、phiが350ではなく200まで減っていたとしたらどうなるでしょうか。

player_a, player_b = glicko2.Rating(mu=1400, phi=200), glicko2.Rating(mu=1000, phi=200)
print(f'プレイヤーA: mu={player_a.mu:.0f} phi={player_a.phi:.0f}, プレイヤーB: mu={player_b.mu:.0f} phi={player_b.phi:.0f}')

glicko2_rating = glicko2.Glicko2()

# 第一引数に勝者、第二引数に敗者
player_b, player_a = glicko2_rating.rate_1vs1(player_b, player_a)

print(f'プレイヤーA: mu={player_a.mu:.0f} phi={player_a.phi:.0f}, プレイヤーB: mu={player_b.mu:.0f} phi={player_b.phi:.0f}')

出力

プレイヤーA: mu=1400 phi=200, プレイヤーB: mu=1000 phi=200
プレイヤーA: mu=1246 phi=191, プレイヤーB: mu=1154 phi=191

1400→1246と、減少は154に留まりました。

ゲームを始めたばかりのプレイヤーはレーティングの変動が大きく、試合をすればするほどだんだん変動が小さくなって落ち着いてくるようになっています。

たとえばMMORPGのGuild Wars 2のPvPにおいて、このGlicko2が用いられていると明言されています。⁶また、公式に名言はされていませんがスプラトゥーンのレーティングにおいてもGlicko2を応用した仕組みが使われていると推測されています。⁷

TrueSkill

TrueSkill は、Microsoftが開発したレーティングシステムです。アイデアはGlickoと似ていて、プレイヤーの強さは平均 $\mu$ 標準偏差 $\sigma$ ⁸の正規分布として表現されます。

名称	初期値	数式上の記号	説明
平均	25	$\mu$（mu）	強さ
標準偏差	25/3=8.333...	$\sigma$（sigma）	強さの振れ幅

Glickoの時と同様に、初期値でグラフにすると下記のような分布になります。

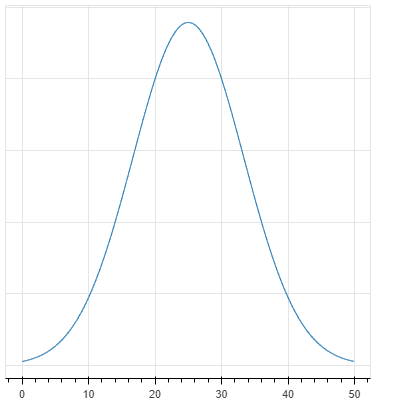
グラフ表示用のコード

import numpy
from scipy.stats import norm

xs = numpy.arange(0, 50, 0.1)
ys = norm.pdf(xs, 25, 25/3)

p = figure(plot_width=400, plot_height=400, y_axis_location=None)
p.line(xs, ys)

show(p)

面白いのは、これらの値はゲーム上では隠しパラメータ扱いであり、ゲーム上のリーダーボードで表示するランク数値⁹は別という点です。
ランク数値の計算式はmu - 3 * sigma、つまり3σ（約99.7%）信頼区間の最低値という「悲観的に見積もった」値を取ります。デフォルトでは平均値μ=25と分散σ=25/3であり、ランク数値は25-3*25/3つまり0ピッタリから始まります。
試合をすると勝敗にかかわらず分散は減少していくので、最初の方は試合に負けてもランク数値が上昇する時があります。

実際に見てみましょう。

import trueskill
trueskill_rank = lambda player: float(player.mu - 3 * player.sigma)

player_a, player_b = trueskill.Rating(), trueskill.Rating()

print(f'プレイヤーA: rank={trueskill_rank(player_a):.2f}, sigma={player_a.sigma:.2f}, プレイヤーB: rank={trueskill_rank(player_b):.2f}, sigma={player_b.sigma:.2f}')

player_a, player_b = trueskill.rate_1vs1(player_a, player_b)

print(f'プレイヤーA: rank={trueskill_rank(player_a):.2f}, sigma={player_a.sigma:.2f}, プレイヤーB: rank={trueskill_rank(player_b):.2f}, sigma={player_b.sigma:.2f}')

出力

プレイヤーA: rank=0.00, sigma=8.33, プレイヤーB: rank=0.00, sigma=8.33
プレイヤーA: rank=7.88, sigma=7.17, プレイヤーB: rank=-0.91, sigma=7.17

Aが勝ってBが負ける同じ試合を5回繰り返してみます。

trueskill_rank = lambda player: float(player.mu - 3 * player.sigma)

player_a, player_b = trueskill.Rating(), trueskill.Rating()

for _ in range(5):
    print(f'プレイヤーA: rank={trueskill_rank(player_a):.2f}, sigma={player_a.sigma:.2f}, プレイヤーB: rank={trueskill_rank(player_b):.2f}, sigma={player_b.sigma:.2f}')
    player_a, player_b = trueskill.rate_1vs1(player_a, player_b)
print(f'プレイヤーA: rank={trueskill_rank(player_a):.2f}, sigma={player_a.sigma:.2f}, プレイヤーB: rank={trueskill_rank(player_b):.2f}, sigma={player_b.sigma:.2f}')

出力

プレイヤーA: rank=0.00, sigma=8.33, プレイヤーB: rank=0.00, sigma=8.33
プレイヤーA: rank=7.88, sigma=7.17, プレイヤーB: rank=-0.91, sigma=7.17
プレイヤーA: rank=11.66, sigma=6.52, プレイヤーB: rank=-0.80, sigma=6.52
プレイヤーA: rank=13.93, sigma=6.11, プレイヤーB: rank=-0.57, sigma=6.11
プレイヤーA: rank=15.48, sigma=5.81, プレイヤーB: rank=-0.34, sigma=5.81
プレイヤーA: rank=16.62, sigma=5.59, プレイヤーB: rank=-0.14, sigma=5.59

Aのランク数値が増え続けるのもそうですが、負け続けているBのランク数値も最後には増えています。

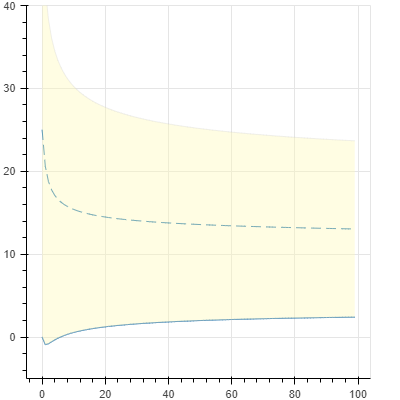
実際に、Bのレーティング mu の 3σ の信頼区間の範囲がどうなっているかを、グラフにして見てみましょう。
Aと100回試合して100回負けたデータを作って、

player_a, player_b = trueskill.Rating(), trueskill.Rating()

results = []

for x in range(100):
    results.append({
        "x": x,
        "b_mu": player_b.mu,
        "b_3sigma_upper": player_b.mu + 3 * player_b.sigma,
        "b_3sigma_lower": player_b.mu - 3 * player_b.sigma,
    })
    player_a, player_b = trueskill.rate_1vs1(player_a, player_b)

グラフにしてみます。

import pandas
from bokeh.models import Band, ColumnDataSource
from bokeh.plotting import figure, show

source = ColumnDataSource(pandas.DataFrame(results))
p = figure(plot_width=400, plot_height=400, y_range=(-5, 40))

p.line("x", "b_mu", source=source, line_dash=(10, 5))
p.line("x", "b_3sigma_lower", source=source)
p.add_layout(Band(base="x", lower="b_3sigma_lower", upper="b_3sigma_upper", source=source))

show(p)

青い点線が mu、黄色い区間が 3σ の範囲です。下部の青い実線がランク数値 mu - 3 * sigmaです。100回負け続けているのですが試合する毎に信頼区間が狭まっていくため、最初の数回を除いてランク数値が緩やかに上昇していることが分かります。

TrueSkillはMicrosoftが開発したもので、Halo 3、Forza Motorsport 7などで採用されている事が明言されています。¹⁰TrueSkillはMicrosoftが特許を持っており通常は商用利用ができないため、Microsoft以外のゲームで目にすることは無いかもしれません。

EloやGlickoはもともとチェスのレーティングを想定して開発されたそうです。そのため1vs1を想定して作られています。
TrueSkillはオンラインゲームのために開発されたようで、1vs1ではなく、4vs4のようなチーム戦や、1vs1vs1vs1のようなバトルロイヤル形式の試合にも適用できる事です。また、オンラインゲームで実力の近いプレイヤー同士をマッチングさせることを想定して、マッチングの品質（引き分けになる確率をもとに算出されているようです）も定義されています。

各レーティングの収束の早さ

Elo Rating、Glicko Rating、TrueSkillの3つの手法を紹介してきました。これらの手法はそれぞれ以前の手法を改善しながら作られて来たのですが、改善された点のひとつにレーティングの収束の早さがあります。
例えば、とても強いプレイヤーでもゲームを始めたばかりの時はデフォルトのレーティング数値から開始します。より少ない試合回数で高いレーティングに安定するようになる手法ほど、収束が早いと言えます。

簡単なプログラムでざっくりと比較してみましょう。プレイヤーA、B、Cの3人で合計1,000回試合をして、レーティングの変化をグラフにしてみます。A>B>Cの順番で強いとして、レーティングの変化がどうなるか見てみます。

実際のコード

def plot_results(results):
    source = ColumnDataSource(pandas.DataFrame(results))
    p = figure(plot_width=400, plot_height=400)

    p.line("x", "player_a", legend_label="player A", source=source, line_color="indigo")
    p.line("x", "player_b", legend_label="player B", source=source, line_color="olivedrab")
    p.line("x", "player_c", legend_label="player C", source=source, line_color="tomato")

    show(p)

# Elo Rating
player_a, player_b, player_c = elo.Rating(), elo.Rating(), elo.Rating()

results = []
for x in range(1000):
    results.append({
        "x": x,
        "player_a": float(player_a),
        "player_b": float(player_b),
        "player_c": float(player_c),
    })

    if x % 3 == 0:
        player_a, player_b = elo.rate_1vs1(player_a, player_b)
    if x % 3 == 1:
        player_b, player_c = elo.rate_1vs1(player_b, player_c)
    if x % 3 == 2:
        player_a, player_c = elo.rate_1vs1(player_a, player_c)

plot_results(results)

# Glicko2 Rating
player_a, player_b, player_c = glicko2.Rating(), glicko2.Rating(), glicko2.Rating()
glicko2_env = glicko2.Glicko2()

results = []
for x in range(1000):
    results.append({
        "x": x,
        "player_a": player_a.mu,
        "player_b": player_b.mu,
        "player_c": player_c.mu,
    })

    if x % 3 == 0:
        player_a, player_b = glicko2_env.rate_1vs1(player_a, player_b)
    if x % 3 == 1:
        player_b, player_c = glicko2_env.rate_1vs1(player_b, player_c)
    if x % 3 == 2:
        player_a, player_c = glicko2_env.rate_1vs1(player_a, player_c)

plot_results(results)

# TrueSkill
player_a, player_b, player_c = trueskill.Rating(), trueskill.Rating(), trueskill.Rating()

results = []
for x in range(1000):
    results.append({
        "x": x,
        "player_a": player_a.mu,
        "player_b": player_b.mu,
        "player_c": player_c.mu,
    })

    if x % 3 == 0:
        player_a, player_b = trueskill.rate_1vs1(player_a, player_b)
    if x % 3 == 1:
        player_b, player_c = trueskill.rate_1vs1(player_b, player_c)
    if x % 3 == 2:
        player_a, player_c = trueskill.rate_1vs1(player_a, player_c)

pandas.DataFrame(results).tail()

plot_results(results)

Elo	Glicko-2	TrueSkill

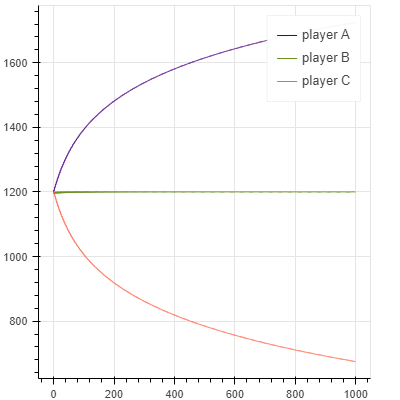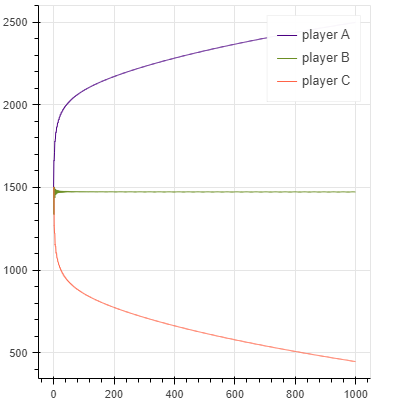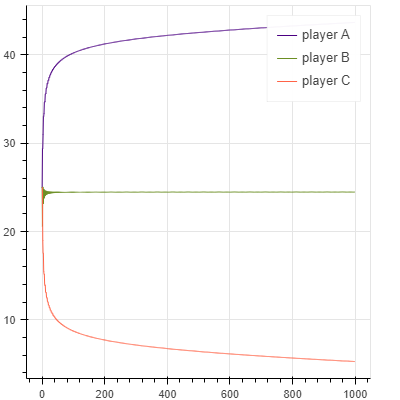スケールも違うので厳密な比較ではないですが、グラフの見た目からEloよりもGlicko-2の方が、Glicko-2よりもTrueSkillの方が、より少ない試合回数で早く収束しているように感じます。手法の改善が進むほどに収束が早くなっていることがわかります。

TrueSkillはゲーム以外にも、学術論文において複数の手法を相対評価する時に用いられる事があります。¹¹このような収束の早さが相対評価の手法として有用だと認められているからかもしれません。

まとめ

直接対決の勝敗結果や勝率のみでは、プレイヤーの強さを正確に表すことはできません。そのため、強さを表すために様々なレーティングシステムが開発されてきました。それぞれの手法はより改善され、プレイヤーの強さ以上にレーティングを不当に高くする行為への対策や、プレイヤー同士の相対的な強さを早く表せるようになったりしていました。これらのレーティングシステムを理解することで、よりゲームが面白くなったり、ゲーム以外でも相対評価が必要な場面において役に立つことがあると思いました。

参考文献

• レイティング・ランキングの数理 - 共立出版
• イロレーティング - Wikipedia
• グリコレーティング - Wikipedia
• TrueSkill - Wikipedia

1. 『スプラトゥーン3』Xマッチが12/1より解禁。ウデマエS+0以上のプレイヤーだけが参加できる、さらなる高みを目指すモード！ | ゲーム・エンタメ最新情報のファミ通.com ↩

2. ゲーム内告知によると実際には2022年12月2日午前9時から ↩

3. 実際には勝敗が決まらない「引き分け」の可能性もあります。本稿では簡単のために原則として引き分けは無いものとします。 ↩

4. レーティングの計算方法と素早さ調整の考え方について徹底解説!!【ポケモン剣盾】 - YouTube ↩

5. これらはsublee/glicko2の内部実装の記号に基づく表記。論文ではこれらの値に補正をかけた後の値にこれらの記号が使われています。 ↩

6. Finding the perfect match – GuildWars2.com ↩

7. splatoon2 のXパワーの仕組みを解説｜はく｜note ↩

8. 実際の文献では分散 $\sigma^2$ で表現されていることが多いが、本稿ではGlicko Ratingと比較しやすくするため標準偏差として用いる。 ↩

9. Microsoftによる解説ページではこのリーダーボード上で表示する数値も「TrueSkill」と呼んでいるが、手法自体の名称と混同してややこしいのでここでは「ランク数値」と呼ぶ。 ↩

10. TrueSkill Ranking System - Microsoft Research ↩

11. 聡一朗村上, 翔星野, and 培楠張. 2022. “広告文自動生成に関する最近の研究動向.” 人工知能学会全国大会論文集 JSAI2022: 1P5GS601–1P5GS601. ↩