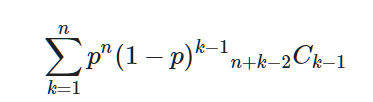背景
最近Pokémon UNITEの大会に参加したりしているんですが、「ダブルエリミネーション方式」「BO3」などの用語がよく分からずに参加していたので、それらの勝率の関係について調べました。
なおこれらの用語は競技によって意味合いや制限が微妙に異なることがありますが、本稿においてはPokémon UNITEのLogStare eSPORTS SERIESおよびPokémon UNITE Winter Tournamentで採用されていた方式に従います。
また本稿ではシードは考慮しない参加人数での開催に限定します。つまり $r$ を正の整数として、トーナメントの参加人数は $2^r$ に限られるものとします。
シングルエリミネーション・BO1
まずはじめに準備として、一般的なトーナメント(いわゆるシングルエリミネーション・BO1)について考えてみます。
┌─ チームA
┌─┤
│ └─ チームB
─┤
│ ┌─ チームC
└─┤
└─ チームD
チームA,B,C,Dの4チームによる、全2ラウンドのトーナメント戦を考えます。
チームAの勝率が60%だとします。より厳密には以下のようになります。
- チームAが、チームB,C,Dに勝つ確率: 60%
- チームB,C,Dが、チームAに勝つ確率: 40%
- チームB,C,Dが互いに戦って勝つ確率: それぞれ50%
このときチームAが優勝する確率は
- 第1回戦(チームB戦) 60%
- 第2回戦(チームCかDのうち第1ラウンドに勝ったほう) 60%
$0.6^2$ で、36%になります。
これを一般化すると、 $2^r$ 人が参加する全 $r$ ラウンドのトーナメントにおいて、勝率 $p$ のチームAが優勝する確率は $p^r$ となります。
ダブルエリミネーション方式
ダブルエリミネーションとは、2回負けたら敗退(Elimination)となる、つまり1回までは負けても続けられる方式です。
以下LogStare eSports Series Pokémon UNITE 大会ルールより引用です。
・「ダブルエリミネーション方式」とは、1度負けたらその時点で敗退となる通常の「シングルエリミネーション方式」とは異なり、2敗した時点で敗退となる大会方式を指す。
・通常のシングルエリミネーショントーナメント(Winners サイド)を行い、1度も敗北しなかったチームが次のマッチに進出する。
・同時に、1敗したチーム同士の間でもシングルエリミネーショントーナメント(Losersサイド)を行い、その後1度も敗北しなかったチームが次のマッチに進出する。
・上記2つのトーナメントを行い、最後まで残った2チームが決勝進出チームとなり、決勝戦を行う。
・すべてのチームは2度敗北しないと、トーナメントから敗退にならないため、決勝戦でLosersサイドを勝ち上がったチームが勝利した場合、決勝の再戦リセットにより、もう1度決勝戦を行い、優勝チームを決定する。
・試合は本タイトルにおける10分のオンライン対戦を指し、マッチはトーナメントにおける勝利チームを決定する対戦を指す。
┌─ チームA
┌─┤
│ └─ チームB
┌─┤
│ │ ┌─ チームC
│ └─┤
│ └─ チームD
─┤
│ ┌─ 1回戦敗者
│ ┌─┤
│ │ └─ 1回戦敗者
└─┤
└─ 2回戦敗者
以下、通常のシングリエリミネーショントーナメントをWinnersと呼び、いちど負けたチーム同士が戦うトーナメントをLosersとします。またWinnersとLosersを勝ち抜いたチームが戦うマッチを決勝戦と呼びます。
計算式
さて、$2^r$ 人が参加する全 $r$ ラウンドのダブルエリミネーション方式トーナメントにおいて、勝率 $p$ のチームAが優勝する確率を計算します。
チームAが優勝するのは以下a,b,c,dの4パターンに分けられます。
a) Winnersで r 連勝し、決勝戦でも1勝するとき
無敗で優勝するパターンです。
$$
p^{r+1}
$$
b) Winnersで r 連勝し、決勝戦で1回負けて、1回勝つとき
Winnersを勝ち抜いたという事は1回も負けていないので、決勝戦で1回負けても敗退とならず、もう1回Loserを勝ち抜いたチームと戦うことになり、そこで勝てば優勝となります。(ほかのすべてのチームが2回負けたことになるので)
$$
p^r(1-p)p
$$
c) Winners第1回戦で負けて、Losers を 2r-2 回勝って、決勝戦で2回勝つとき
ここから少しややこしくなります。Losersのトーナメントの最大試合数は $2r-2$ 回となります。
| 参加人数 $2^r$ | $r$ | Losers試合回数 |
|---|---|---|
| 4 | 2 | 2 |
| 8 | 3 | 4 |
| 16 | 4 | 6 |
| $2^r$ | $r$ | $2r-2$ |
Winnersで1度も勝てなかった場合は、Losersの $2r-2$ 回すべて勝って、さらに決勝戦でWinnersを勝ち上がったチームに2回勝たないといけません。
$$
(1-p)p^{2r-2}p^2
$$
d) winnersで w 回勝って(w>=1)、第 w+1 回戦で負けて、losers を 2(r-w)-1 回勝って、決勝戦で2回勝つとき
Winnersで1回でも勝った場合、勝った回数を $w$ とおくと、Losersでの残り試合数は 2(r-w)-1 となります。Winnersの同じラウンドで負けた人同士の対戦からはじまるのはLosers1回戦のみだから、その1回が無い分試合数が減ります。
wが1からr-1までの場合について、この確率の総和を取ったものが、このパターンの勝率になります。
(w=rはWinnersで優勝しているため、このパターンに含まれない)
$$
{\sum_{w=1}^{r-1}p^w(1-p)p^{2(r-w)-1}}p^2
$$
これは等比数列の和の公式を使うと、以下のように変形できます。
$$
(p^r-p^{2r-1})p^2
$$
チームAが優勝する確率
以上a,b,c,dの4つをすべて足すと、以下の式になります。
$$
2p^{r+1}-2p^{2r+1}+p^{2r}
=2p^{r+1}+p^{2r}(1-2p)
$$
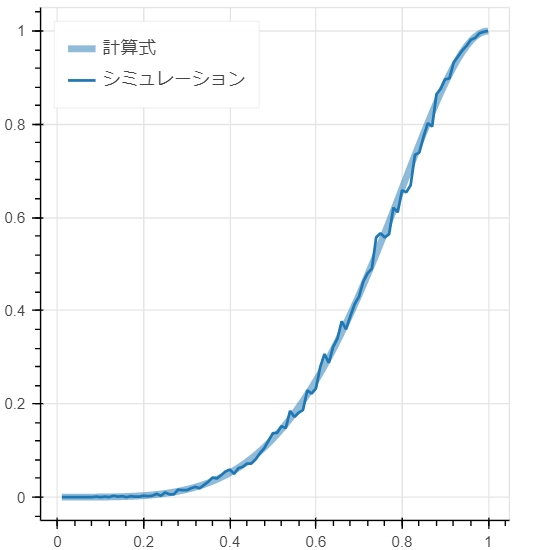
自信が無いので検算
この計算式に自信がないので、シミュレーションした結果と計算式による結果を突き合わせてチェックしました。
def double_elimination_tournament(battle = lambda: random() < 0.6, rounds=2):
# winners
for winners_round in range(rounds):
if not battle():
# losers
for loosers_round in range(2 * (rounds - winners_round) - 1):
# winners1回戦敗退の場合は試合数を1回減らす
if (winners_round == 0) and (loosers_round == 0):
continue
if not battle():
return False
# losers final
if battle():
if battle():
return True
return False
# winners final
if battle():
return True
else:
if battle():
return True
return False
raise Exception
def simulate_double_elimination(p=0.5, r=3, times=100000):
battle = battle = lambda: random() < p
results = simulation(tournament=lambda: double_elimination_tournament(battle, rounds=r), times=times)
return results["win"] / (results["win"] + results["lose"])
だいたい合っているような気がします。
考察
こちらの数式をPythonのBokehで可視化してみます。
from bokeh.io import output_notebook, show
from bokeh.plotting import figure
output_notebook()
# トーナメント優勝確率の数式
def formula_single_elimination(p=0.5, r=3):
return p**(r)
def formula_double_elimination(p=0.5, r=3):
return 2*p**(r+1) + (p**(2*r))*(1 - 2*p)
# グラフの描画
dots = 100
rounds = 6
xs = [ (x+1)/dots for x in range(dots) ]
p = figure(plot_width=400, plot_height=400)
ys1 = [ formula_double_elimination(p=x, r=rounds) for x in xs ]
p.line(x=xs,
y=ys1,
line_width=5,
line_alpha=0.5,
legend_label="ダブルエリミネーション"
)
ys2 = [ formula_single_elimination(p=x, r=rounds) for x in xs ]
p.line(x=xs,
y=ys2,
line_width=2,
legend_label="シングルエリミネーション"
)
p.legend.location = "top_left"
p.xaxis.axis_label = '1ラウンドあたり勝率p'
p.yaxis.axis_label = '優勝する確率'
show(p)
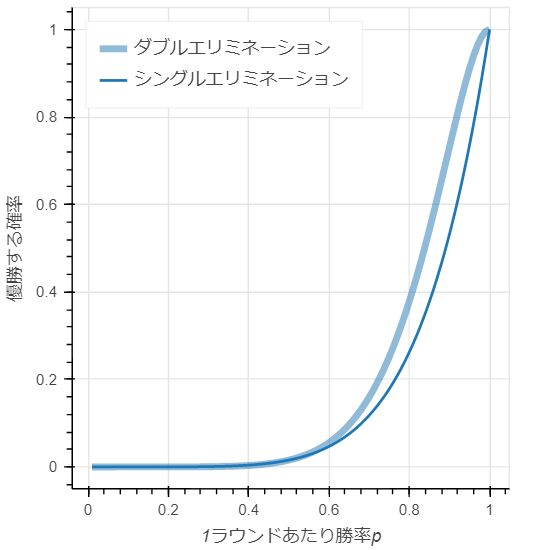
r=6(64人参加)のトーナメントにおいて、1ラウンドあたり勝率pのチームがトーナメントで優勝する確率のグラフが下記です。
ダブルエリミネーションの方が、より勝率の高いチームが優勝しやすい、つまり 優勝結果に実力が反映されやすい ことが分かります。
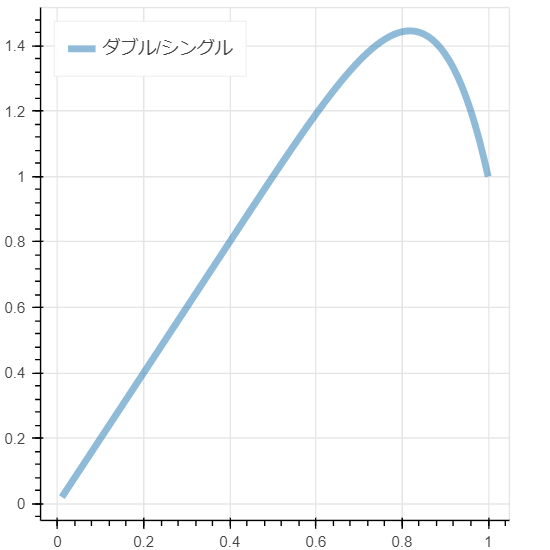
ダブルエリミネーションの勝率を、シングルエリミネーションの勝率で割ったグラフが以下になります。
pが0.5以上ならば、ダブルエリミネーションの方が優勝しやすく、その割合はp=0.8付近で最も大きくなります。
一方で、勝率が100%に限りなく近い圧倒的な強さを持っている場合はどっちにしろ優勝するので、試合回数が多くなるダブルエリミネーションでもそこまで結果は変わらないことが分かります。
BO3
BO3は「Best of 3」の略で、「3試合2本先取」のことです。『Pokémon UNITE』 Winter Tournamentなどで採用されています。
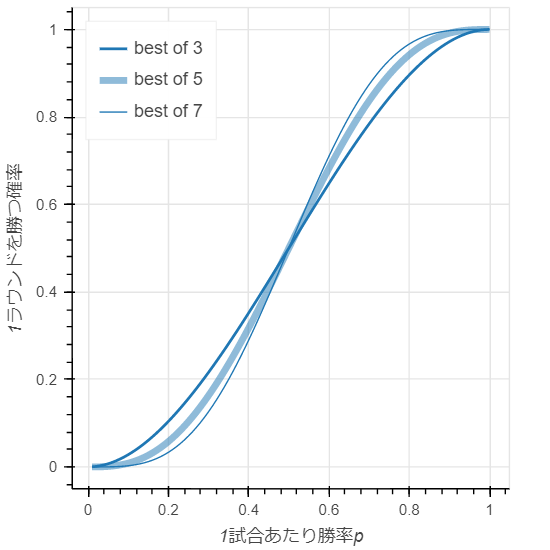
BO1は通常の1発勝負、BO3は2本先取、BO5は3本先取...というように、BO$2n-1 (n > 0)$はn本先取となり、その勝率は下記になります。
考察
こちらも下記プログラムでグラフにしてみます。
# 計算式
def best_of_x(n=3,p=0.5,verbose=0):
if verbose > 0:
print(f'best of {2*n-1}')
return sum([ p**n * (1-p)**(k-1) * combinations_count(n+k-2, k-1) for k in range(1, n+1) ])
# グラフ描画
dots = 100
xs = [ (x+1)/dots for x in range(dots) ]
p = figure(plot_width=400, plot_height=400)
best_of_x_n = 2
ys1 = [ best_of_x(n=best_of_x_n, p=x) for x in xs ]
p.line(x=xs,
y=ys1,
line_width=2,
legend_label=f"best of {2 * best_of_x_n - 1}"
)
best_of_x_n = 3
ys2 = [ best_of_x(n=best_of_x_n, p=x) for x in xs ]
p.line(x=xs,
y=ys2,
line_width=5,
line_alpha=0.5,
legend_label=f"best of {2 * best_of_x_n - 1}"
)
best_of_x_n = 4
ys3 = [ best_of_x(n=best_of_x_n, p=x) for x in xs ]
p.line(x=xs,
y=ys3,
line_width=1,
legend_label=f"best of {2 * best_of_x_n - 1}"
)
p.legend.location = "top_left"
p.xaxis.axis_label = '1試合あたり勝率p'
p.yaxis.axis_label = '1ラウンドを勝つ確率'
show(p)
BO3よりBO5の方が、BO5よりBO7の方が、勝率が高いチームほど勝ち上がりやすいという事が分かります。
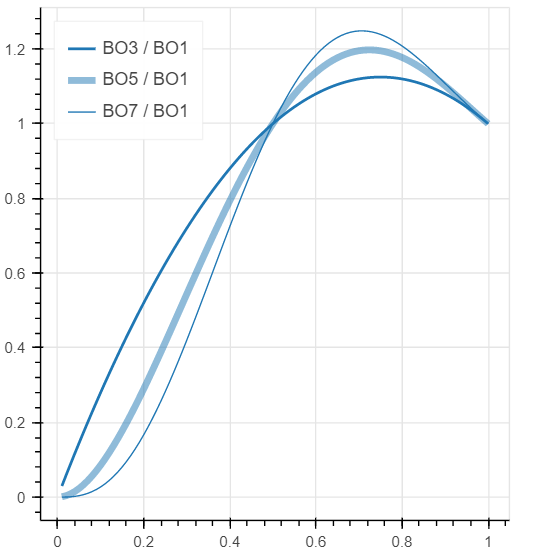
各勝率を、BO1の勝率(つまりp)で割ったもののグラフは以下です。
同じ相手との試合における戦術の変更
ここまで、チームの勝率pは常に一定であるとしてきました。しかし、BO3というのは同じ相手と連続して試合する事になりますので、1回負けても2回目は戦術を変更できます。2
チームAは「2つの戦術を使い分けることでリスクをコントロールできる」ものとしましょう。同じ相手に1回負けたら相手の方が格上であると判断して、よりリスクの高い戦術、勝つか負けるか分からないけど五分五分に持ち込めるかもしれないような戦術を採用する、とします。3対戦相手の戦術は変わらないものとします。
ここで、リスクとは勝率50%にどれだけ近いか(50%に近いほどリスクが大きい戦術)と定義し、本来の戦術の勝率 $p_1$ に対して、高リスク戦術 $p_2=(p_1-0.5)/2 + 0.5$ と定義します。
| 通常勝率 $p_1$ | 高リスク戦術勝率 $p_2$ |
|---|---|
| 80% | 65% |
| 60% | 55% |
| 50% | 50% |
| 40% | 45% |
| 20% | 35% |
# p1は低リスク戦術、p2は高リスク戦術
def best_of_3_risks(p1=0.8, risk_rate=2, verbose=0):
p2 = (p1 - 0.5)/risk_rate + 0.5
if verbose > 0:
print(f'p1={p1}, p2={p2}')
return p1**2 + p1*(1-p1)*p2 + (1-p1)*p2*p2
best_of_3_risks(p1=0.8, verbose=1)
# グラフ描画
dots = 100
xs = [ (x+1)/dots for x in range(dots) ]
p = figure(plot_width=400, plot_height=400)
ys1 = [ best_of_3(p=x) for x in xs ]
p.line(x=xs,
y=ys1,
line_width=2,
legend_label=f"best of 3"
)
ys2 = [ best_of_3_risks(p1=x) for x in xs ]
p.line(x=xs,
y=ys2,
line_width=5,
line_alpha=0.5,
legend_label=f"best of 3 (1度負けたら高リスク戦術)"
)
p.legend.location = "top_left"
show(p)
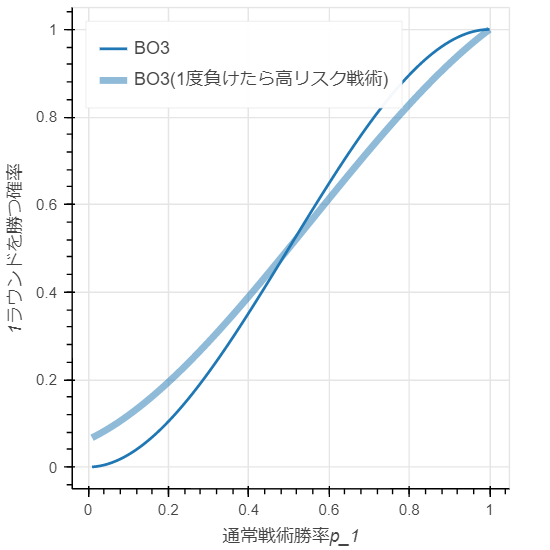
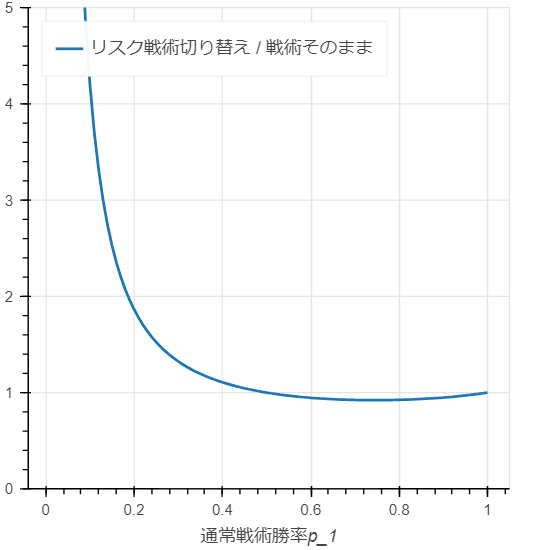
さらに、戦術を切り替えた場合の勝率を、戦術を切り替えないで戦った場合の勝率で割ったグラフが下記です。
勝率が50%を超えている場合は、戦術を切り替えてもさほど勝ち抜ける確率は変わりません。
一方で、勝率が低い場合に勝ち抜ける確率が大きく変わる事が分かります。
よって、格上の相手と戦う場合など通常の戦術による勝率がとても低いと分かった時に、なんとかして勝ち抜きたいならば、リスクの高い戦術に切り替える事ができれば勝ち抜ける確率が大きく上がるだろうという事が分かります。。
結論
- 勝率が高いほど優勝しやすい
- 勝率が高いと、シングルエリミネーションよりもダブルエリミネーションの方が優勝しやすい
- 勝率が高いと、BO1よりもBO3やBO5の方が勝ち抜きやすい
- 勝率が低い場合、BO3において一度負けたらリスクの高い戦術に切り替えることができればその方が勝ち抜きやすい
- こんな計算をしている暇があったら練習試合をしたほうが優勝しやすい
参考
またトーナメント表の作成にはトーナメント作成ツール を利用しました。