2020年夏、量子コンピューターのクラウドサービスである**Amazon Braket**が一般公開されました。本稿では巡回セールスマン問題を、Amazon Braketを使って量子コンピューターで解いてみます。
量子コンピューターとは
量子コンピューターとは、量子物理学の特性を活用した新しい仕組みのコンピューターのことです。量子コンピューターについて語る文脈においては、それに対して2020年現在私達が一般的に使っている"普通の"コンピューターのことを、「古典物理学に基づいている」という意味で古典コンピューターと呼びます。「古典」と言われると古い感じがしますが、私達が今使っているパソコンもスマホも全部古典コンピューターに分類されます。
古典コンピューターでは、0か1かの状態をとる古典ビットをつかって情報(いわゆる"変数")を表現します。それに対して、量子コンピューターでは量子の「重ね合わせ」の性質を使うことで、0と1の両方の状態を同時に表現できる量子ビットを使って計算を行います。
そのため古典コンピューターと量子コンピューターはまったく扱い方が異なり、C言語やJavaなど既存のプログラミング言語で量子コンピューターを扱うこともできません。ですが、量子コンピューターを使うことで計算量のオーダーを削減できる方法がいくつも考案されており、うまく使うことで従来の古典コンピューターではとても現実的な時間で解けなかった問題が解けるようになります。
量子コンピューターは2020年現在はまだ研究段階の技術ですが、後述するAmazon Braketのようにクラウドサービスを使って一般にも利用できるようになってきています。
量子ゲート方式と量子アニーリング方式
量子コンピューターには、大きく分けて量子ゲート方式と量子アニーリング方式の2つがあります。
量子ゲート方式は「万能型」とも呼ばれます。たとえば古典コンピューターであれば、0か1かのいずれかの状態を取る古典ビットに対して、ANDゲートやORゲート等の論理ゲートを作用させて処理をしていきます。それに対して量子ゲート方式の量子コンピューターでは、0と1の両方の状態を同時に取る量子ビットに対して、パウリXゲートやアダマールゲートといった量子ゲートを組み合わせて処理していきます。ゲートの作用が古典コンピューターとは全く異なりますが、ビットとゲートを使うという点に注目すれば、私達がイメージするコンピューターのように汎用的に処理を組み立てられます。ですが、量子ゲート方式は2020年現在の技術では数十個程度の量子ビットしか扱うことができないようです。
一方で量子アニーリング方式は「特化型」とも呼ばれ、量子ビットの安定状態を探索するという、特定の計算にしか使うことができません。その代わり数千個の量子ビットを使って計算できるのが特徴です。
本稿では量子アニーリング方式について、もう少し詳しく見てみます。
量子アニーリング方式のイジングモデル
量子アニーリング方式の量子コンピューターの説明には**イジングモデル(イジング模型、Ising Model)**を使います。動作をイメージするために、少し簡略化して説明していきます。
イジングモデルとは統計力学で磁石などの説明に使われるモデルです。+1(上向き)または-1(下向き)のいずれかの状態をとる量子ビットを格子状に配置した物で、隣接するビット同士には相互作用が、それぞれのビットには局所磁場が作用します。
例えばふたつの量子ビットがあって相互作用が+1の時、両方の量子ビットが+1どうし又は-1同士だとエネルギーが大きく"不安定"な状態になります。
片方が+1でもう片方が-1だとエネルギーが小さくなって"安定"します。
磁石をイメージしてください。N極の隣にS極が隣接していると安定しますが、N極とN極とが隣接していると反発しあって不安定な状態になり、"N極とS極とが隣接している状態"にひっくり返りたがるように働きます。
ふたつの量子ビットどうしの相互作用が-1だった場合は関係性が逆になり、両方の量子ビットが+1どうし又は-1どうしだった場合に安定します。
ここまでを数式で表してみましょう。ふたつの量子ビット$i,j$があって、それらの向きを+1か-1かの値を取る変数$x_i,x_j$で、それら$i,j$ふたつの間の相互作用を$Q_{ij}$とします。これらのエネルギーを求める式は以下となります。
Q_{ij}x_ix_j
この式の値が小さいほど、ふたつの量子ビットは安定している状態と言えます。
ここで厳密ではない式変形を使いますが、このエネルギーを全ての量子ビットに対して合計します。
H = \sum_{i,j} Q_{ij}x_ix_j
このようにモデル上の全部のエネルギーを計算した式は一般にハミルトニアンと呼ばれ、$H$で表されます。$H$が最も小さい値になる状態が安定状態です。
たくさんの量子ビットがあった時に、エネルギーが最も小さくなって安定する状態を求めることができるのが量子アニーリング方式の量子コンピューターです。つまり、ある「解きたい問題」があった時、それを適当なパラメータ$Q$を使って問題をイジングモデルに対応させられれば、最適解となる変数$q$を量子コンピューターで求める事ができます。
先に述べたとおり、上記の式変形は厳密な物ではありませんので注意してください。また実際には、変数の値は-1か+1か、ではなく0か1か、のバイナリ変数を取るように式変形して利用することが多いようです。
Amazon Braketとは
Amazon Braket (量子コンピューティングの深堀と実験) | AWS
Amazon Braketとは、量子ゲート方式・量子アニーリング方式の両方の量子コンピューターをフルマネージド型クラウドとして使えるようにしたサービスです。
Amazon Braketでは(古典コンピューターである)SageMakerのJupyter Notebook環境を構築できます。このJupyter Notebook環境にはaws/amazon-braket-sdk-pythonというフレームワークが予めセットアップされており、このSDKによってAmazon Braketの様々な量子コンピューターをPythonから操作できるようになっています。
つまり開発者はPythonプログラムを与えられたJupyter Notebook上で記述するだけで、Amazon Braketの量子コンピューターを使えるというわけです。
Amazon Braketで使える量子コンピューター
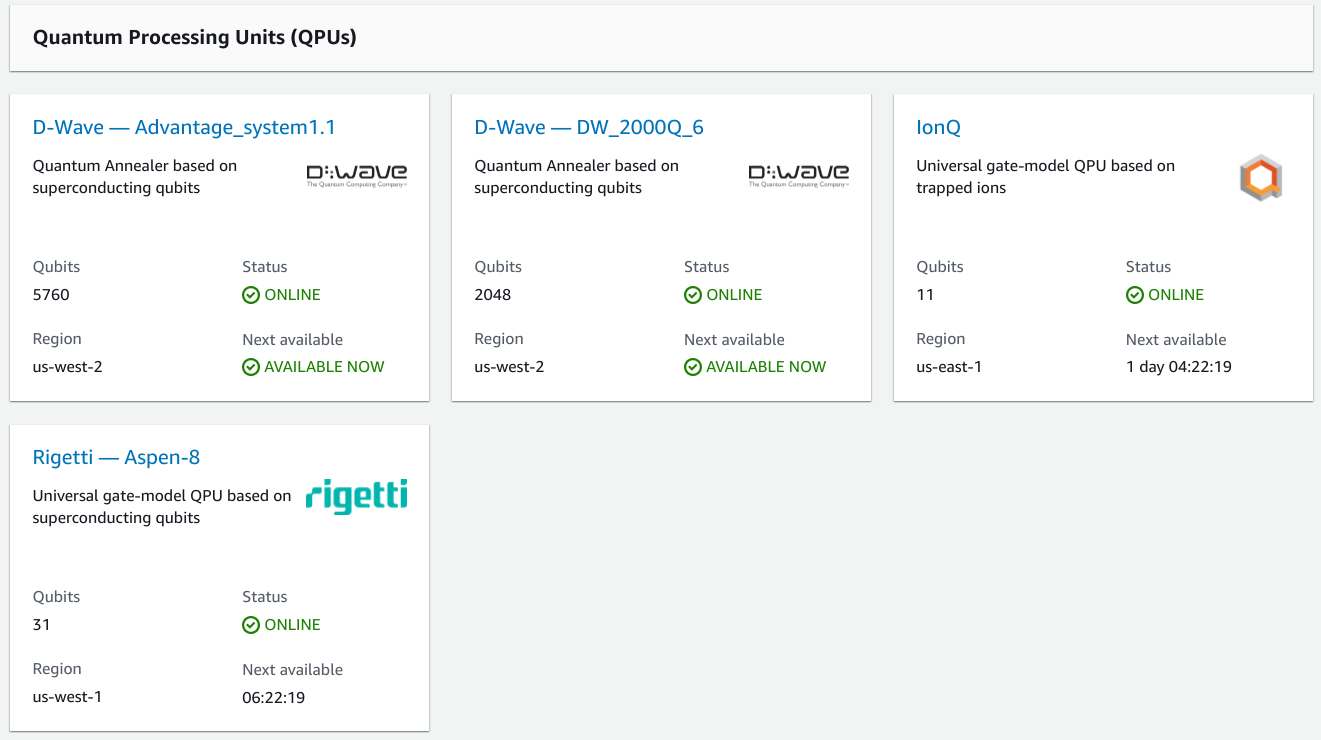
Amazon Braketで使える量子コンピューターは2020年11月現在Rigetti、IonQ、D-Waveの3種類が使えるようになっており、それぞれのマシンに"ARN"というAWS上の一意なリソース識別子が付与されています。つまり、普通のEC2仮想マシンやS3サービスと同じようなノリで量子コンピューターを呼び出して扱えるようになっているというわけです。例えばDW_2000Q6のARNはarn:aws:braket:::device/qpu/d-wave/DW_2000Q_6となっています。
それぞれの量子コンピューターは特定のリージョンにしか配置されていません。他に大きな特徴として、すべての量子コンピューターが24時間いつでも使えるわけではなく、特定の時間帯にしか利用できない物もあります。そういった利用に制限のある量子コンピュータのテスト用として、AWS EC2上に構築された古典コンピューターによるシミュレーターAWS SV1も用意されており、いつでも使うことができます。
2020年11月現在Amazon Braketで利用できる量子コンピューター一覧(AWS SV1は量子コンピューターではない)
| - | D-Wave Advantage_system1.1 | D-Wave DW2000Q_6 | IonQ | Rigetti Aspen-8 | AWS SV1 |
|---|---|---|---|---|---|
| 方式 | 量子アニーリング方式 | 量子アニーリング方式 | 量子ゲート方式 | 量子ゲート方式 | 古典コンピューター |
| 量子ビット数 | 5,760 | 2,048 | 11 | 38 | 34 |
| 利用可能時間 | いつでも | いつでも | 平日13時〜21時 (UTC) | 毎日15時〜19時 (UTC) | いつでも |
| 料金 | $0.30/task + $0.00019/shot | $0.30/task + $0.00019/shot | $0.30/task + $0.01/shot | $0.30/task + $0.00035/shot | $4.5/hour |
| リージョン | us-west-2 | us-west-2 | us-east-1 | us-west-1 | us-east-1, us-west-1, us-west-2 |
本稿ではD-Waveを使った例を紹介します。
巡回セールスマン問題とは
巡回セールスマン問題(Traveling Salesman Problem、TSP) とは、いくつかの都市と、都市間の距離が与えられた時に、すべての都市を一度ずつ訪問する最短のルートを求める問題です。
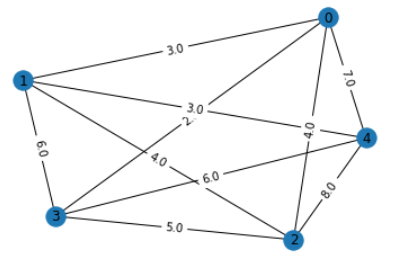
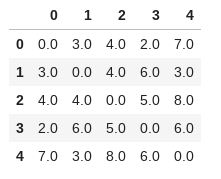
下記の画像の例だと「0,1,2,3,4」の5個の都市と、それらの距離とが示されています。例えば0と1のあいだの距離は3、0と2の距離は4、0と3の距離は2、0と4の距離は7、といった具合です。0,1,2,3,4のすべての都市を通る閉路を見つけるのがTSPです。
TSPは古典コンピューターでも多くの厳密解法および近似解法が研究されていますが、一般に都市の数が多くなればなるほどパターンの数が爆発的に増加するため、計算に大きな時間がかかると言われています。
量子アニーリング方式でTSPを解く
以下に掲載する定式化手法およびプログラムのソースコードは、AmazonがGitHubで公開しているAmazon Braket Examplesからの引用です。Amazon BraketでJupyter Notebookインスタンスを構築すると、似ている(恐らく同一の)内容のプログラムがセットアップされていて、すぐ使うことが出来ます。
イジングモデルでの定式化
例えば都市が東京・大阪・名古屋の3つだったとして、東京=1,大阪=2,名古屋=3のようにインデックスを付けます。
「都市$i$を$j$番目に訪れるとき1、そうでない時0」となる変数$x_{ij}$で、巡回のルートを表します。例えば東京→名古屋→大阪の順番でめぐるならば、$x_{11}=1,x_{32}=1,x_{23}=1$となり、ほかは全部ゼロとなるバイナリ行列で順回路を表現できます。
X = \begin{pmatrix}
1 & 0 & 0\\
0 & 0 & 1\\
0 & 1 & 0\\
\end{pmatrix}
この$X$を探索対象の変数として定式化します。都市$i,j$間の距離を計算した行列$D$を用いて、$k$番目から$k+1$番目に移動するときの距離コストを、以下のように表現できます。
D_{ij} \sum_{k} x_{i,k}x_{j,k+1}
$x_{i,k}x_{j,k+1}$は、都市$i$の次に訪れるのが都市$j$だった場合のみ1になります。これを全ての都市間$i,j$について合計した値が、この順回路$x$の距離になります。
H_{\text{dist}} = \sum_{i,j} D_{ij} \sum_{k} x_{i,k}x_{j,k+1}
この$H_{\text{dist}}$を最小化すれば良いのですが、この定式化には問題があります。変数$x$について何の制限も課していないため、$x$は全部ゼロにすれば良い、となってしまいます。
実際には「すべての都市は一度だけ訪れる」「すべての順番は一度だけ登場する」というふたつの制約条件を$x$に課す必要があります。
ラグランジュ緩和法による制約条件の表現
制約条件をイジングモデルで表現するために、量子コンピューター関係無く一般の数理最適化問題においても使われる事がある**ラグランジュ緩和法(Lagrangean Relaxation Method)**を使います。
例えば、最小値を求めたい目的関数$f(x_1, x_2)$に対して、$x_1 + x_2 = 0$という制約条件があった場合、$f(x_1, x_2)$を最小化するのではなく、適当な定数$P$を用意して$f(x_1, x_2) + P(x_1 + x_2)^2$を最小化する問題である、というように書き換えます。制約条件を無くして"緩和"しているため"緩和法"と呼ばれます。
$(x_1 + x_2)$が制約を破ってゼロから離れた値になってしまうと、$f(x_1, x_2) + P(x_1 + x_2)^2$の値が大きくなってしまい、目的関数に対してペナルティが与えられます。定数$P$が大きければ大きいほど、制約をちょっと破っただけでもペナルティが大きくなり、実質的に制約条件を守らないと最適解が得られなくなってしまいます。この時の$P$を**ラグランジュペナルティパラメータ(Lagrange penalty parameter)または単にラグランジュパラメータ(Lagrange parameter)**と呼ぶことがあります。
ラグランジュパラメータ値は、ペナルティの値が本来最小化したい値$f(x_1, x_2)$の平均値の近くになるよう設定されます。実際には**ハイパーパラメータ最適化(Hyper Parameter Optimization、HPO)**の手法で探索されることもあります。
さて、巡回セールスマン問題(TSP)に話を戻します。以下は、先に紹介した「東京→名古屋→大阪の順で訪れることを示す行列」をイメージすると理解しやすいと思います。
X = \begin{pmatrix}
1 & 0 & 0\\
0 & 0 & 1\\
0 & 1 & 0\\
\end{pmatrix}
「すべての都市は一度だけ訪れる」「すべての順番は一度だけ登場する」というふたつの制約条件が必要でした。まず前者から。この制約条件は、ある都市に対応する変数はひとつだけ1で残り全部0という事なので、任意の都市$i$に対して($\forall i$と表記)以下が成り立つこと、と表現できます。
\sum_j x_{ij} = 1\: (\forall i)
変数行列で言えば「すべての行は和が1になる」と言っているのと同様です。
この制約条件を緩和して、ラグランジュパラメータを用いて目的関数(巡回路の距離の総和)に以下のペナルティを与えること、とできます。
P\sum_i(\sum_j x_{ij} - 1)^2
同様に、「すべての順番は一度だけ登場する」という制約条件は、任意の順番$j$に対して
\sum_i x_{ij} = 1\: (\forall j)
と表現できます。「すべての列は和が1になる」と言っているのと同様です。これによって、以下のようなペナルティを与えることで制約条件を緩和できます。
P\sum_j(\sum_i x_{ij} - 1)^2
以上より、制約(constraint)は以下のように表されます。
H_{\text{constraint}} = P\sum_i(\sum_j x_{ij} - 1)^2 + P\sum_j(\sum_i x_{ij} - 1)^2
最適化対象のハミルトニアン$H$は、以下のように表現できます。
\begin{eqnarray}
H &=& H_{\text{dist}} + H_{\text{constraint}} \\
&=&\sum_{i,j} D_{ij} \sum_{k} x_{i,k}x_{j,k+1} + P\sum_i(\sum_j x_{ij} - 1)^2 + P\sum_j(\sum_i x_{ij} - 1)^2
\end{eqnarray}
これにて、TSPをイジングモデルに対応させることができました。
Amazon Braketで量子コンピューターを使う
Amazon Braket自体のセットアップはAWSに慣れていれば難しくありませんので、環境構築についての詳細は本稿では割愛します。クラスメソッド社の紹介記事などを参考にしてください。
AccessDeniedExceptionが出た場合
もしプログラムの実行時に「AccessDeniedException: An error occurred (AccessDeniedException) when calling the GetDevice operation: User is not authorized to perform: braket:GetDevice」のようなエラーが出た場合、Amazon Braket有効化時に作成したIAMロールに「AmazonBraketFullAccess」を付与すれば実行できるようになります。
D-Waveで巡回セールスマン問題を解く
Amazon BraketでのSageMakerインスタンス構築時に、巡回セールスマン問題(TSP)を解くプログラムはサンプルとしてJupyter Notebook内に初期状態で配置されています。
Amazon BraketのJupyter Notebookを作成・起動したら、Braket examples/quantum_annealing/Dwave_TSP_Braket/のディレクトリにあるTSP_D-Wave_Braket_tutorial_imports.ipynbのファイルを開きます。あとはこのNotebookのPythonプログラムを実行すればTSPが解けるのですが...以下にてすこし解説します。
まず都市間の距離データがテキストで配置されているので、読み込みます。
data = pd.read_csv('Braket examples/quantum_annealing/Dwave_TSP_Braket/tsp_data/five_d.txt', sep='\s+', header=None)
data
このデータでは5つの都市があり、たとえば都市0と都市1のあいだの距離は3.0のようです。
この都市データを使って、TSPで言う都市を点(node)、都市間を結ぶ道を枝(edge)としたグラフを生成します。
G = nx.from_pandas_adjacency(data)
pos = nx.spring_layout(G, seed=seed)
nodes = G.nodes()
edges = G.edges()
weights = nx.get_edge_attributes(G,'weight');
グラフは下記コードで可視化して確認できます。
plt.axis('off');
nx.draw_networkx(G, pos, with_labels=True);
nx.draw_networkx_edge_labels(G, pos, edge_labels=weights);
グラフから、量子アニーリング方式でTSPを定式化する関数は下記になります。$H =\sum_{i,j} D_{ij} \sum_{k} x_{i,k}x_{j,k+1} + P\sum_i(\sum_j x_{ij} - 1)^2 + P\sum_j(\sum_i x_{ij} - 1)^2
$を展開して、$H = \sum_{i,j} Q_{ij}x_ix_j$の係数の行列$Q$を求めています。
def traveling_salesperson_qubo(G, lagrange, weight='weight'):
# 都市の数
N = G.number_of_nodes()
# 量子ビットを生成
Q = defaultdict(float)
# 「すべての都市は一度だけ訪れる」制約の項
for pos in range(N):
for node_1 in G:
Q[((node_1, pos), (node_1, pos))] -= lagrange
for node_2 in set(G)-{node_1}:
Q[((node_1, pos), (node_2, pos))] += lagrange
# 「すべての順番は一度だけ登場する」制約の項
for node in G:
for pos_1 in range(N):
Q[((node, pos_1), (node, pos_1))] -= lagrange
for pos_2 in range(pos_1+1, N):
Q[((node, pos_1), (node, pos_2))] += 2.0*lagrange
# 最適化対象となる、距離を求める項
for u, v in itertools.combinations(G.nodes, 2):
for pos in range(N):
nextpos = (pos + 1) % N
# u -> v
Q[((u, pos), (v, nextpos))] += G[u][v][weight]
# v -> u
Q[((v, pos), (u, nextpos))] += G[u][v][weight]
return Q
ここで得られた行列$Q$を用いて、以下のtraveling_salesperson()関数でTSPを解きます。samplerというのは後述しますが、D-Waveの量子コンピューターへの接続情報を持っています。(やっと出てきましたね量子コンピューター)
def traveling_salesperson(G, sampler=None, lagrange, weight='weight',
start=None, **sampler_args):
Q = traveling_salesperson_qubo(G, lagrange, weight)
response = sampler.sample_qubo(Q, **sampler_args)
sample = response.first.sample
route = [None]*len(G)
for (city, time), val in sample.items():
if val:
route[time] = city
if start is not None and route[0] != start:
# スタート地点を最初に持ってくる
idx = route.index(start)
route = route[idx:] + route[:idx]
return route
以下のようにsamplerオブジェクトを生成してtraveling_salesperson()へ渡します。
arn:aws:braket:::device/qpu/d-wave/Advantage_system1が、D-Waveの量子コンピューターのARNです。
sampler = BraketDWaveSampler(s3_folder,'arn:aws:braket:::device/qpu/d-wave/Advantage_system1')
sampler = EmbeddingComposite(sampler)
# パラメータの設定
num_shots = 1000
start_city = 0
best_distance = sum(weights.values())
best_route = [None]*len(G)
# 計算
route = traveling_salesperson(G, sampler, lagrange=lagrange,
start=start_city, num_reads=num_shots, answer_mode="histogram")
# 結果の出力
print('---FINAL SOLUTION---')
print('Best solution found with D-Wave:', best_route)
print('Total distance (including return):', best_distance)
これを実行した所、以下のような解の出力が得られ、巡回セールスマン問題を解くことができました!
Best solution found with D-Wave: [0, 1, 4, 2, 3]
Total distance (including return): 21.0
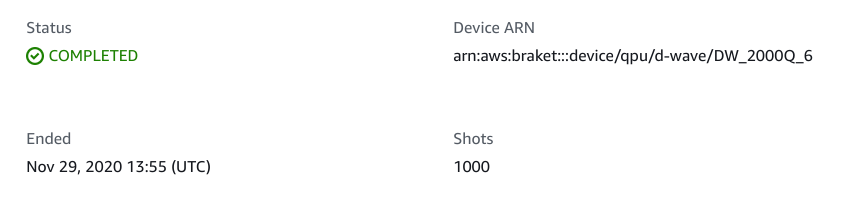
AWS管理コンソール上で、使った量子コンピューターと同じリージョンのAmazon Braket Tasksを開くと、下記のように実行完了状態になっている事が確認できると思います。
(※"使った量子コンピューターと同じリージョン"というのは、"SageMakerノートブックインスタンスのあるリージョン"と必ずしも一致しません)
まとめ
Amazon Braketを使って、量子アニーリング方式の量子コンピューターを用いて巡回セールスマン問題を解くことができました。こういった事が、AWSというクラウドサービスで個人でも気軽に実行できるようになりました。
本稿で示した例は都市数が少なく、古典コンピューターを使っても十分な速度で解を得ることができます。ですがより複雑な問題になっても量子コンピューターで解くことができるようになり、量子コンピューターの性能が古典コンピューターを上回る**量子超越性(Quantum Supremacy)**が示されれば、今まで解くことの難しかった問題が解けるようになると思います。量子コンピューターの発展に期待しましょう。
参考文献
-
このプログラミング言語がすごい!:ビーチーム | 技術書典マーケット
- 宣伝ですが、拙稿(第7章)にて本Qiita記事では触れなかった「量子ゲート方式(万能型)」のプログラミング言語Q#について紹介しています。
- いちばんやさしい量子コンピューターの教本 人気講師が教える世界が注目する最新テクノロジー - インプレスブックス
- 絵で見てわかる量子コンピュータの仕組み(宇津木 健 徳永 裕己)|翔泳社の本
- グラフ分割問題 をD-Wave 2000Qで解く(実践編) - T-Wave
- 物理のいらない量子アニーリング入門 - Platinum Data Blog by BrainPad