エイチームフィナジーアドベントカレンダー1日目は私 s2terminal が担当します。私は普段Web開発やデータサイエンスの仕事していますが、その中でWebサイトに掲載する商材の口コミを集計したり、社内行事で表彰制度の投票集計に携わったりすることで ランキング という物に触れる機会が多少ありました。
先日、弊社グループ内で大規模なLT大会が開催されました。そこではLTの視聴者による投票が行われ、最も良かったLTのランキングを決めることになりました。その際に私は、ランキングのアルゴリズムの設計・実装を担当しました。
本稿では、単純なランキング集計にはどういう問題点があるかと、このLT大会において「良いLT」が上位になるようなランキングをどのように考えたかを書きます。LT大会のランキングを題材としていますが、たとえばECサイトの星5段階評価からランキングを考える場合などにも応用できると思います。本稿に於ける手法は完璧な物ではありませんが実際に利用されたものであり、何かの参考になれば幸いです。
なお参考までに、弊社グループのLT大会のレポート記事を掲載します。(この記事は2020年に開催されたものですが、本稿で対象としているのは2021年開催したLT大会になります)
投票で順位を決めることの難しさ
まず「投票によってランキングを作る」事を考える前に、この問題の難しさについて説明します。投票制度設計について「ある"良い"条件を満たすような投票制度は作れない」という 不可能性定理 がいくつか知られています。その中でもノーベル経済学賞を受賞したケネス・アロー(Kenneth Joseph Arrow)による アローの不可能性定理 を紹介します。これは、以下に示すような条件をすべて同時に満たすような投票制度は作れない、というものです。
-
定義域の非制限性(Unrestricted domain)
- 投票者は選択肢に対して自由に投票できる
-
無関係な選択肢からの独立性(Independence of Irrelevant Alternatives、IIA)
- ある投票者の部分集合の中でAよりもBが良いという結論になったら、他の選択肢によってその結果が変わることはない
- 例えば、他の選択肢Cが失格となって候補から消えたとしても、AよりもBが良いという結論が変わってはいけない
-
パレートの原則(Pareto efficiency、全会一致の原則)
- すべての投票者がAよりもBが良いと投票した時、AよりもBのほうがランキングが上になる
-
非独裁制(Non-dictatorship)
- ランキングを左右するような独裁的な権限を持っている投票者がいてはならない
どの条件も、"良い"投票制度を設計しようと考えた時に満たすべき条件として違和感は無いと思います。ですが、これらをすべて満たすような制度は設計できないという事が証明されています。
理論的な話は省いて、もう少しイメージしやすい具体例を挙げてみます。「じゃんけんの手{グー, チョキ, パー}の中から最強はどれか?」を投票で決めるという問題を考えてみてください。
投票の結果「グーに投票した人が最も多かったので、グーが最強」と言われたとしたら、どう思いますか?「パーならグーに勝てるから、最強ではない」と納得のいかない人が必ず出てきます。この問題は、投票では誰もが納得行くような結果にすることはできません。
このように、多くの条件を満たす理想的な投票ランキングを設計するのは難しいことが知られています。完璧なランキングはそもそも作れないので、大切なのは 「どういう選択肢が上位に来るようなランキングにしたいか?」を考えて、アルゴリズムを設計・選択すること だと思います。
LT大会の前提条件
具体的な説明に入る前に、今回の「LT大会」および「投票」がどんなものだったか、前提条件を定義しておきます。おそらく「投票システムがあるLT大会」として一般的にイメージされるような物と相違は無いのでは、と思います。
- LT大会の進行について
-
ブレイクアウトセッション形式を採用
- (同時に複数トラックに分かれてセッションが行われ、視聴者は任意の時間帯に好きなセッションを自由に選んで見ることができる)
- すべてのトラックでセッションの開始時間・終了時間は同じとする(セッションの長さはすべて同じで、開始時間がズレて重なったりするケースは無い)
-
ブレイクアウトセッション形式を採用
- 視聴者について
- 視聴者はLT大会の途中参加・途中退室が認められている
- つまり、すべての時間帯でセッションを見るとは限らず、時間帯によってセッションを閲覧しない・投票しないこともある
- 視聴者はLT大会の途中参加・途中退室が認められている
- 投票について
- 視聴者は、見たセッションそれぞれが良かったかどうかについて5段階で評価できる
- 数字が大きいほど「良い」とする
また、理論的な条件に関係は無いのですがランキングを考える上で注意すべき前提として、これは 社内でのLT大会であり、LT発表者も視聴者もすべて社内のスタッフ(身内)に限定されている という点を改めて明記しておきます。これにより、例えば5段階評価の偏りに影響が出てきます。LT大会開催前から出ていた仮説として、社内のスタッフに対して厳しい評価を投票する人は少なく、多くの人は高い数値を投票するのでは?と想定されました。
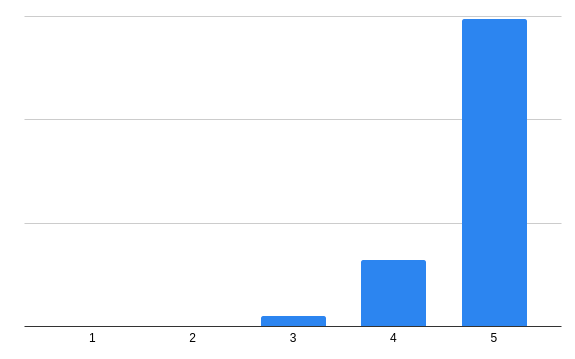
▲実際のLT大会後に集計した5段階評価別の投票数。約8割の人が「5」を投票し、「1」を投票した人はいませんでした。
単純なアルゴリズムの例とその問題点
実際に、LT大会の投票とランキングについて考えていきます。
LT大会のランキングとは、セッション $i$ に対してレーティング $r_i$ を"良い感じ"に定義し、すべてのセッションのレーティングのベクトル $\boldsymbol{r}=\{r_1,r_2,...,r_n\}$ の各要素を高い順に並べたもの、とします。パラメータとして、セッション $i$ を見た視聴者 $h$ による5段階評価ポイント $p_{hi} \in \{1,2,3,4,5\}$ が与えられますので、これをうまく使って $r_i$ を定義することで、より"良い"ランキングを求めたい、という問題です。
数式ばかりだとイメージしにくいですので、最初は単純なランキングアルゴリズムを具体例として挙げ、その問題点を述べていきます。
5段階評価ポイントの合計点
まずは最も単純な「5段階評価の合計点」で順位を決めてみましょう。一応数式を書くとこういう事です。
$$
r_i = \sum_{h}{p_{hi}}
$$
たとえば、3つのセッションがあるLT大会を開催し、投票結果が下記のようになったとします。
| 視聴者 | セッション1 | セッション2 | セッション3 |
|---|---|---|---|
| Aさん | 2 | 2 | - |
| Bさん | 2 | 2 | - |
| Cさん | 2 | 2 | - |
| Dさん | 2 | 2 | - |
| Eさん | 2 | - | 5 |
このときレーティングは各セッションの合計点なので、以下のようになります。
| - | セッション1 | セッション2 | セッション3 |
|---|---|---|---|
| レーティング | 10 | 8 | 5 |
| ランキング | 1位 | 2位 | 3位 |
この結果を見て、どうでしょうか。
A〜Dさんは何も思わないかもしれませんが、Eさんからすると「セッション1よりもセッション3のほうが内容が良かったのに、視聴者が少なかったせいでランキングが上がらなかった」と不満を持つことになります。たくさんの人が来たほうが有利 となってしまいます。
5段階評価ポイントの平均点
次に、評価の平均値を取ってみましょう。
$$
r_i = \frac{1}{n}\sum_{h}{p_{hi}}
$$
これならば、合計点による問題「たくさんの人が視聴したセッションが有利になる」を解消できると思います。ですが、これだと「みんなセッション1よりもセッション2のほうが良いと言っているのに、セッション1のほうが上位に来る」という現象が起きてしまいます。たとえば極端なケースとして、下記のような例を見てみましょう。
| 視聴者 | セッション1 | セッション2 | セッション3 |
|---|---|---|---|
| Aさん | 5 | 5 | - |
| Bさん | 5 | 5 | - |
| Cさん | 5 | - | - |
| Dさん | 5 | - | - |
| Eさん | 2 | 3 | 4 |
| - | セッション1 | セッション2 | セッション3 |
|---|---|---|---|
| レーティング | 4.4 | 4.33... | 4.0 |
| ランキング | 1位 | 2位 | 3位 |
Eさんからすると、セッション1よりもセッション2のほうが、セッション2よりもセッション3のほうが良かったですし、A~Dさんとしても異論はありません。ですが順位は逆になってしまいました。5段階評価の基準は視聴者それぞれの主観的なものなので、単純に平均値を取ると 高い数値の評価をする人が多く集まったセッションが有利 となってしまいました。
先に述べたとおり特に今回は社内のLT大会ですので、多くの人は4や5の高い数値を投票するのでは?と想定されました。すると上記の例のように、大多数の人が高い数値を投票する中で、少しだけいる低い数値を投票する人が見に行ったセッションが不利となってしまうことが予想されました。
これまでのアルゴリズムの問題点
これら2つのアルゴリズムの問題点は「セッションを聞いた人」に依存してしまう点だと思います。今回ランキングを考える上で、「どういう人がセッションを聞いたか?」ではなくて、できるだけ 「セッションの中身が良かったかどうか?」で順位を決めたい と思い、別のアルゴリズムを考えることにしました。
ところで、たとえば「中身の良いセッションならば、たくさんの人が聞きに来ているはずだ」という仮定を置くならば、単純な合計点によるランキングでも機能すると思います。これまでに挙げたランキング決定方法は間違っているわけではありません。重要なのは「どういう選択肢がランキング上位に来てほしいか?」をケースによってできるだけ反映できるように設計することだと思います。
5段階評価ポイントの相対評価によるランキング
実際に採用したランキングアルゴリズムについて述べていきます。「良いセッションが上位に来るランキングになってほしい」を実現するために、今回は 相対評価 に着目しました。
例えば、ある人がA・Bふたつのセッションを見て「AよりもBのほうが良かった」と思ったとき、この人はどういう投票をするか考えてみます。
- Aに1、Bに5
- Aに3、Bに4
- Aに2、Bに3
...などなど色々なパターンが考えられますが、とにかく 「AよりもBのほうが良かったならば、AよりもBに対して高い点をつけるだろう」 というのは自然な発想です。この数値に着目してランキングを作れば、少なくとも投票した人に対して納得感の得やすいランキングが実現できるのではないか、と思いました。
計算
実際の詳細な計算は『レイティング・ランキングの数理』1という本を参照してほしいのですが、プログラムの実装に必要な概要のみ記載します。
まず、セッション $i,j$ の両方を見た人の集合を $H_{ij}$ とし、 $H_{ij}$ によるセッション $i$ の評価について考えます。 $H_{ij}$ の人数を $n_{ij}$ として、$j$ に対する $i$ の評価スコアを以下のように定義します。
$$
s_{ij} = \frac1{n_{ij}}{\sum_{h \in H_{ij}}p_{hi}}
$$
若干ややこしい表現を使いましたが、要するに $i,j$ の両方を見た人に限定した平均値であり、ここまでは先述の単純な方法と大きな変わりはありません。
この平均値評価スコアをすべてのセッションについて計算した行列 $\boldsymbol{S} = [s_{ij}]$ を用いて、$j$ に対する $i$ の相対評価を、$i,j$ 両方の平均値の差を取った $k_{ij}=s_{ij}-s_{ji}$ とします。相対評価スコアによる行列 $\boldsymbol{K} = [k_{ij}]$ を定義すると、以下のように計算できます。
$$
\boldsymbol{K} = [k_{ij}] = [s_{ij} - s_{ji}] = \boldsymbol{S}-\boldsymbol{S}^T
$$
"良い感じ"にランキング算出用のレーティングベクトル $\boldsymbol{r}$ 定義することで、この相対評価スコア行列 $\boldsymbol{K}$ を表してほしいわけです。"良い感じ"の $\boldsymbol{r}$ を求めたいので $\boldsymbol{r}$ を変数として、レーティングベクトルについても相対評価スコア行列 $\boldsymbol{K}$ と同様に $i,j$ 間の相対評価を取った行列 $\boldsymbol{R(r)}=[r_i-r_j]$ を定義します。$\boldsymbol{R(r)}$ が $\boldsymbol{K}$ に近くなるような時、つまり
$$
f(\boldsymbol{r})=||\boldsymbol{K}-\boldsymbol{R(r)}||^2
$$
この $f(\boldsymbol{r})$ が最小になるような $\boldsymbol{r}$ が、相対評価 $\boldsymbol{K}$ を最もよく反映しているレーティングのベクトルになります。これを計算2すると以下の結果になります。
$$
\boldsymbol{r} = \frac{1}{n}{\boldsymbol{Ke}}
$$
上記 $\boldsymbol{r}$ を計算して数値の大きい順に並べることで、ランキングが得られます。これは相対評価スコア行列 $\boldsymbol{K}$ の、列に対する平均を取ったものです。表現としてはややこしくなりましたが、5段階評価の平均値を算出し、その差を取って、さらに平均したものと言われると、実際の計算としてはシンプルです。
実装
実際にプログラムで計算してみましょう。
今回LT大会の投票はGoogleフォームを使ってリアルタイムで投票されていきました。そのデータをスプレッドシートのピボットテーブルを使って「どの視聴者がどのセッションに何点を投票したか」というテーブルに集計しました。それをPythonのプログラムにて行列データにして処理しました。
今回の要件として順位を求めるのはすべてのセッションが完了した後の1回だけでOKだったので、スプレッドシートからGoogleColabへ手動で貼り付けましたが、リアルタイムでの順位計算が求められる場合はAPIを使って連携などする必要があると思います。
またデータ量について、今回は事前にテストして10,000件以上の投票データがあっても集計がうまくいく事は確認していましたが、不特定多数に投票してもらう場合など大量の投票データがある場合はこの方法ではうまく行かないかもしれません。
例として、4つのセッションからなるLT大会に10人の視聴者が下記のような投票をしたとします。
| 視聴者 | セッション1 | セッション2 | セッション3 | セッション4 |
|---|---|---|---|---|
| 視聴者1 | 4 | 2 | 2 | - |
| 視聴者2 | 3 | 1 | - | 2 |
| 視聴者3 | 1 | - | 2 | - |
| 視聴者4 | 2 | 4 | 2 | - |
| 視聴者5 | - | 3 | 2 | 5 |
| 視聴者6 | 2 | 3 | - | - |
| 視聴者7 | - | 4 | 1 | 3 |
| 視聴者8 | 3 | 1 | 1 | - |
| 視聴者9 | - | 3 | 2 | 5 |
| 視聴者10 | 2 | - | 2 | 4 |
これをPythonのプログラムで以下のように定義されるようにしておきます。
import numpy
from numpy import NaN
data = numpy.array([
[4,2,2,NaN],
[3,1,NaN,2],
[1,NaN,2,NaN],
[2,4,2,NaN],
[NaN,3,2,5],
[2,3,NaN,NaN],
[NaN,4,1,3],
[3,1,1,NaN],
[NaN,3,2,5],
[2,NaN,2,4],
])
下記のようなプログラムで、実際に $\boldsymbol{r} = \frac{1}{n}{\boldsymbol{Ke}}$ を求められます。
# a,b両方にスコアが存在する部分のみaから抜き出した行を作る
def intersection_values(a, b):
return a[~numpy.isnan(a) * ~numpy.isnan(b)]
# 平均値スコア行列Sを作る
def score_matrix(data):
reviewee_count = data.shape[1]
s = []
for pi in range(reviewee_count):
sr = []
for pj in range(reviewee_count):
if pi == pj:
sr.append(0)
continue
hij = intersection_values(data[:,pi], data[:,pj])
nij = hij.size
sij = (hij.sum() / nij if nij != 0 else 0)
sr.append(sij)
s.append(sr)
return numpy.array(s)
# 相対評価レーティングベクトルを返す
def relative_score_rating(data):
reviewee_count = data.shape[1]
s = score_matrix(data)
# 相対評価Kを求める
k = s - s.T
# 平均値を求める
return k @ numpy.ones(reviewee_count) / reviewee_count
先程のデータでrelative_score_rating(data)を実行するとarray([ 0.175 , -0.10833333, -1.06666667, 1.0 ])という結果になります。
| - | セッション1 | セッション2 | セッション3 | セッション4 |
|---|---|---|---|---|
| レーティング | 0.175 | -0.10833333 | -1.06666667 | 1.0 |
| ランキング | 2位 | 3位 | 4位 | 1位 |
参考までに、同じデータに対して合計値と平均値でレーティングを算出した時のランキングについても記載しておきます。
| - | セッション1 | セッション2 | セッション3 | セッション4 |
|---|---|---|---|---|
| 合計値によるレーティング | 17 | 21 | 14 | 19 |
| 合計値によるランキング | 3位 | 1位 | 4位 | 2位 |
| 平均値によるレーティング | 2.42857143 | 2.625 | 1.75 | 3.8 |
| 平均値によるランキング | 3位 | 2位 | 4位 | 1位 |
合計値によるランキングは、最も視聴者数が多かったセッション2が1位となりました。また、セッション3も視聴者数が多かったのですが低い投票点数ばかりだったので有利を活かしきれず4位となりました。
平均値によるランキングは、相対評価によるランキングと近いものになっていますが、セッション1とセッション2の順位が入れ替わっています。セッション1と2を両方見たという人は5人いて
- セッション1のほうが、セッション2よりも良かったと言っている人は3人
- セッション2のほうが、セッション1よりも良かったと言っている人は2人
相対評価によるランキングはセッション1が2位、セッション2が3位となっており、この2つのセッションを見た人たちの意見をより反映しているといえると思います。
課題
この相対評価によるランキングについては完璧なものではなく、以下のような問題点もありました。
- 1つのセッションしか見てない人の投票を加味できない
- この相対評価に反映されるには、最低でも2つのセッションに対して投票する必要があります
- 同点が多く出る問題への根本的な解決になっていない
- 「多くの人が5を入れるだろう」という状況は変わっておらず、そうなると相対評価で差を取っても0点になるケースが多くなるため、同点が多く出る事への根本的な解決にはなっていません
- 一応「ランキングが同点だった場合は投票者の投票時刻の分散がより小さい方(より即答で評価されたほう)を上位とする」等のロジックは用意しておいて最終的に順位が必ず決まるようにしていましたが、幸い実際に使うことはありませんでした
- この問題に対処するには「1つのセッションに対して5段階評価する」という投票の方法を変える必要があると思います
- ランキング上位のトラックに偏りが出た
- 実際のLT大会ではトラック毎に大まかなジャンルが設定されていたのですが、ランキング上位に特定のトラックのセッションが集中しました
- ジャンルの異なるトラック間での相対評価がうまく機能しなかった可能性があります
まとめ
本稿では相対評価を用いたランキング導出のアルゴリズムと、その実装や課題について紹介しました。
ランキングアルゴリズムについては本稿で紹介した以外にも様々な物があります。ランキングを設計する際は「どういう選択肢が上位に来て欲しいか?」を考えて設計すること、完璧なランキングは作れないということを頭に入れながらアルゴリズムを選択・設計すると良いと思います。
参考文献
- 『レイティング・ランキングの数理 ―No.1は誰か?』 / Amy N.Langville Carl D.Meyer 著 岩野 和生 中村 英史 清水 咲里 訳 | 共立出版
- 『Google PageRankの数理 ―最強検索エンジンのランキング手法を求めて―』 / Amy N.Langville Carl D.Meyer 著 岩野 和生 黒川 利明 黒川 洋 訳 | 共立出版
- 『はじめてのゲーム理論』(川越 敏司)ブルーバックス|講談社BOOK倶楽部
- 『Amazonランキングの謎を解く』 株式会社 化学同人
-
https://www.kyoritsu-pub.co.jp/bookdetail/9784320123908 第10章「ユーザープレファレンスのレイティング」参照 ↩
-
行列ノルムをフロベニウスノルムとして微分した結果得られる。また制約として $\sum_i\boldsymbol{r}_i=0$ を追加することで定数を除去している。 ↩