【機械学習】sklearnによる多項式回帰(Polynomial Regression)の実践

はじめに

sklearnで多項式回帰を実践してみました。

多項式回帰とは

多項式回帰は、二次関数や三次関数のような、次数の高い曲線的な分布のデータ予測を行うための手法です。
単回帰分析だとデータの分布に沿った一次関数の直線を引くことができますが、そういったケースはなかなかありません。
そのため、一次関数で直線的な関係がyとxに見られないときには多項式回帰を使います。

PolynomialFeatures

sklearnで多項式回帰を行う際、PolynomialFeaturesで多項式や交互作用の特徴量を生成します。
例えば、特徴量[A,B,C]があった場合、PolynomialFeaturesで[A, B, C, A^2, A * B, A * C, B^2, B * C, C^2]が生成されます。

from sklearn.preprocessing import PolynomialFeatures

polynomial_converter = PolynomialFeatures(degree=2,include_bias=False)
poly_features = polynomial_converter.fit_transform(X)

実践

まずはパラメータ(次数)のチューニングを行うため、以下を実行します。

• 次数を変えてXデータをつくる
• 訓練データとテストデータにわける
• 訓練データにモデルを適用(fit)する
• 訓練とテスト結果の両方についてメトリクスをだす
• 結果をプロットして過学習していないかどうか確かめる

# 次数ごとの訓練データのエラー
train_rmse_errors = []
# 次数ごとのテストデータのエラー
test_rmse_errors = []

for d in range(1,10):
    
    # 次数(d)を変えてXデータをつくる
    polynomial_converter = PolynomialFeatures(degree=d,include_bias=False)
    poly_features = polynomial_converter.fit_transform(X)
    
    # 訓練データとテストデータにわける
    X_train, X_test, y_train, y_test = train_test_split(poly_features, y, test_size=0.3, random_state=101)
    
    # 訓練データにモデルを適用(fit)する(今回はLinearRegression)
    model = LinearRegression(fit_intercept=True)
    model.fit(X_train,y_train)
    
    # 訓練データとテストデータを予測する
    train_pred = model.predict(X_train)
    test_pred = model.predict(X_test)
    
    # 訓練データのエラー(RMSE)を算出する
    train_RMSE = np.sqrt(mean_squared_error(y_train,train_pred))
    
    # 訓練データのエラー(RMSE)を算出する
    test_RMSE = np.sqrt(mean_squared_error(y_test,test_pred))

    # プロット用に次数ごとのRMSEのリストをつくる
    train_rmse_errors.append(train_RMSE)
    test_rmse_errors.append(test_RMSE)

訓練データとテストデータの次数ごとのRMSEリストができたら、その結果をError(RMSE) VS Model Complexity(Polynomial Complexity)としてプロットします。

plt.plot(range(1,10),train_rmse_errors,label='TRAIN')
plt.plot(range(1,10),test_rmse_errors,label='TEST')
plt.xlabel("Polynomial Complexity")
plt.ylabel("RMSE")
plt.ylim(0,100)
plt.legend()

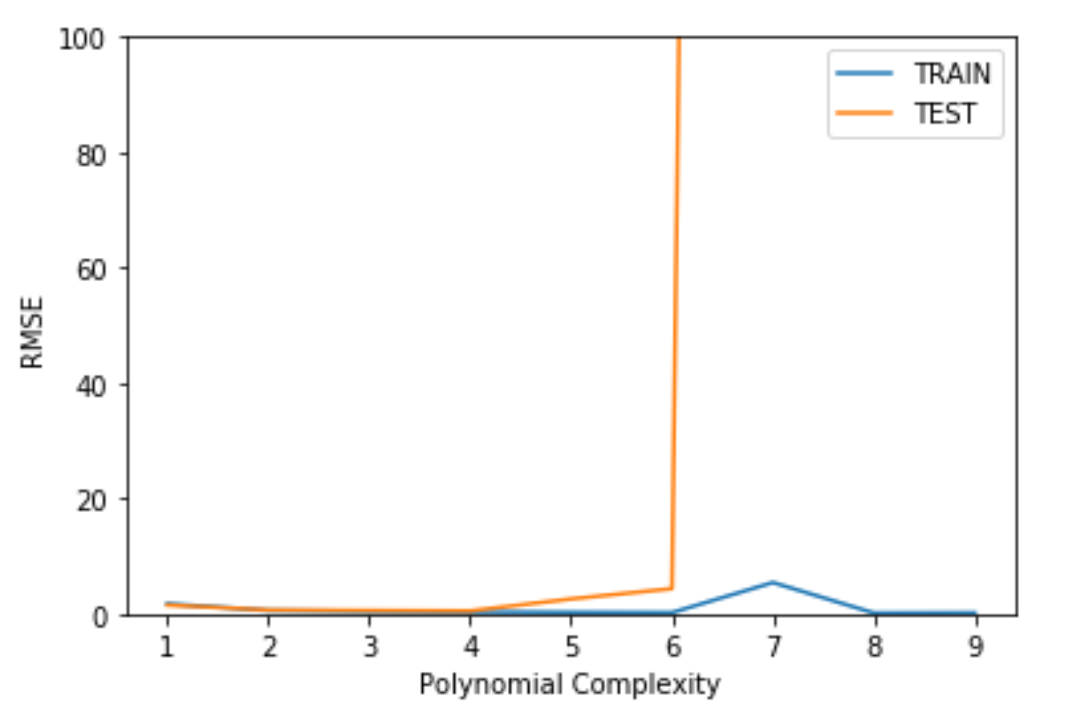
プロットをみると、Polynomial Complexityが6のときにテストデータのErrorが大きくなっています。
これはモデルが訓練データに最適化して過学習(over-fitting)の状態になってしまっている(=バリアンスが大きい)ためにおこります。
次数を小さくすれば過学習の状態を緩和することができますが、これを小さくしすぎると、今度は訓練データさえも正確に予測できない学習不足(under-fitting)の状態になってしまいます。

このように、バリアンス(ばらつき誤差)とバイアス(偏り誤差)には、どちらかを小さくするとどちらかが大きくなるというトレードオフの関係があります。
そのため、両者のバランスが丁度いい最適解を決定する必要があります。

今回のケースでは、次数3を選択します(4でも大丈夫そうですが、より安全な次数を選択します)。

テストのメトリクス(プロット)から最終パラメータ(次数3)を選択したら、モデルの最終決定のために以下を実行します。

• すべてのデータ(訓練+テスト)について再訓練を行う
• Polynomial Converterオブジェクト(Polynomial Featureを生成するオブジェクト)を保存する
• モデルを保存する

#すべてのデータで再訓練
final_poly_converter = PolynomialFeatures(degree=3,include_bias=False)
final_model = LinearRegression()
final_model.fit(final_poly_converter.fit_transform(X),y)

#オブジェクトとモデルを保存
from joblib import dump, load

ump(final_model, 'sales_poly_model.joblib') 
dump(final_poly_converter,'poly_converter.joblib')

保存したオブジェクトやモデルを再度使用する際には、以下のように読み込みます。

loaded_poly = load('poly_converter.joblib')
loaded_model = load('sales_poly_model.joblib')

参考資料