【アルゴリズム】JavaScriptで部分配列問題を解く

#はじめに
Qiitaの競技プログラミング研究月間ということで、アルゴリズムの記事を書いています。
今回は部分配列に関する問題をまとめました。

JavaScriptでアルゴリズムの勉強をされている方の参考になれば幸いです。
記事を順次まとめていきますので、その他の記事についてはマイページからご覧ください。

#チャンク(Chunk)
配列とチャンクサイズを引数で与えたとき、配列内にチャンクサイズと同じ長さの部分配列をつくってください。

chunk([1, 2, 3, 4], 2) --> [[ 1, 2], [3, 4]]
chunk([1, 2, 3, 4, 5], 2) --> [[ 1, 2], [3, 4], [5]]
chunk([1, 2, 3, 4, 5, 6, 7, 8], 3) --> [[ 1, 2, 3], [4, 5, 6], [7, 8]]
chunk([1, 2, 3, 4, 5], 4) --> [[ 1, 2, 3, 4], [5]]
chunk([1, 2, 3, 4, 5], 10) --> [[ 1, 2, 3, 4, 5]]

#解答
以下の処理を考えて実装します。

• 部分配列を包含する空配列chunkedをつくる
• 引数で与えた配列の各要素elementに対してforをまわす
  • chunkedの最後の要素(部分配列)lastを取り出す
  • (if) lastがない、またelementの長さがチャンクサイズと同じ場合
    • chunkedにelementを含んだ配列[element]を追加する
  • (else) 該当しない場合
    • lastにelementを追加する

index.js

function chunk(array, size) {
  const chunked = [];

  for (let element of array) {
    // chunkedの最後の要素(部分配列)
    const last = chunked[chunked.length - 1];

    if (!last || last.length === size) {
      chunked.push([element]);
    } else {
      last.push(element);
    }
  }
  return chunked;
}

#スパイラルマトリクス(SpiralMatrix)
引数に整数Nを与えたときに、NxNのスパイラルマトリクスを返してください。

  matrix(2)
     [[1, 2],
     [4, 3]]
  matrix(4)
     [[1, 2, 3, 4],
     [12, 13, 14, 5],
     [11, 16, 15, 6],
     [10, 9, 8, 7]]

##解答
以下の処理を考えます。
初期値1のcounterという変数をつくって、1ずつ増やしながら部分配列に格納していくイメージとなります。

• 部分配列を包含する空配列resultsをつくる
• counterという変数をつくる(初期値1)
• 1, 2, 3, 4の順番でforを回し、counterを格納する(1ずつ増やしていく)

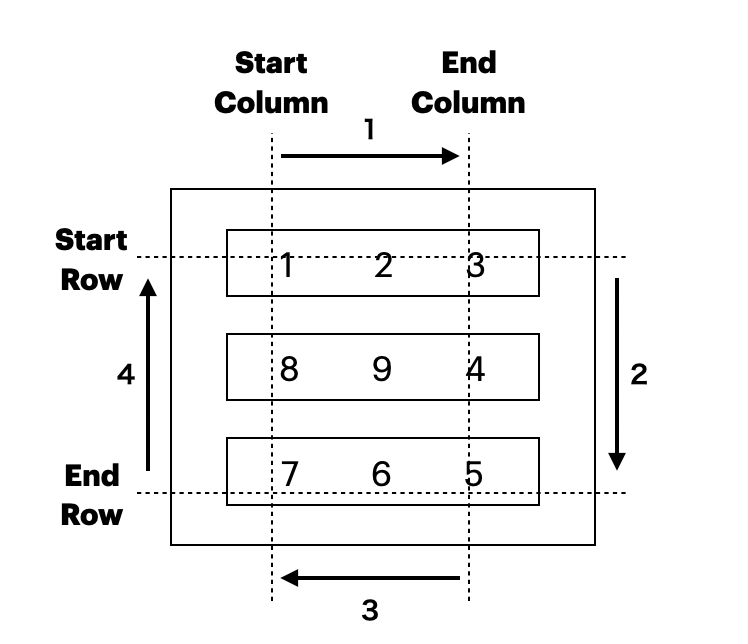
配列resultsには空の部分配列を先に格納してしまい、その後に処理を行っていきます。

index.js

function matrix(n) {
  const results = [];

  for (let i = 0; i < n; i++) {
    results.push([]);
  }

  let counter = 1;
  let startColumn = 0;
  let endColumn = n - 1;
  let startRow = 0;
  let endRow = n - 1;

  while (startColumn <= endColumn && startRow <= endRow) {
    // Top row
    for (let i = startColumn; i <= endColumn; i++) {
      results[startRow][i] = counter;
      counter++;
    }
    startRow++;

    // Right column
    for (let i = startRow; i <= endRow; i++) {
      results[i][endColumn] = counter;
      counter++;
    }
    endColumn--;

    // Bottom row
    for (let i = endColumn; i >= startColumn; i--) {
      results[endRow][i] = counter;
      counter++;
    }
    endRow--;

    // start column
    for (let i = endRow; i >= startRow; i--) {
      results[i][startColumn] = counter;
      counter++;
    }
    startColumn++;
  }

  return results;
}

#参考資料
https://www.udemy.com/share/101WNkCEEZd11VRno=/