数値補間手法の食べ比べ

概要

業務/研究上、別途用意されているデータファイルから読み込み、補間して使うことが多いので補間手法についてかるーくまとめて比較する。
ついでといってはなんだが、所属する団体ではまだまだ情報化が進んでおらずExcelで近似曲線作ってそれから計算するという手法がまかり通っている。それは補間ではない。というわけで関数フィッテングと補間の比較もしてみる。

補間手法

Linear Interpolate

線形補間、1次補間とも。正確にはデータ処理の上では3つ以上のデータが存在することがほとんどなので区分毎に補間する区分線形補間となる。この場合、実は1次スプライン補間となる。
線形補間は接続が滑らかでないので（元から直線で結ばれるデータでもなければ）サンプル点以外の精度が落ちる。これを解消するにはサンプル点を細かくする必要がある。
他に比べて精度が良いわけではないがしばしば利用される補間。その理由は大きいとこで2つ。

• 計算量が少ない
• オーバーシュート/アンダーシュートが生じない

その他の補間では連立方程式を解く必要があることが多いが、線形補間では必要なく以下の式のみで評価できる。したがって補間に必要な計算量は事前に区間の傾きを計算しておくなら$O(n)$となり軽量な計算となる。
（事前にソートして補間時にサーチ、計算すれば$O(logN)$？計算量よくわからん。誰か教えてほしい）

\frac{y-y_0}{y_1-y_0}=\frac{x-x_0}{x_1-x_0}

y=y_0+(x-x_0)\frac{y_1-y_0}{x_1-x_0}

細かい解説はWikipediaにも載ってるしここでは割愛。

3rd Order (Cubic) Spline Interpolate

よく使われる、3次スプライン補間。区間を1次関数で補間するのが1次スプライン、3次の多項式で補間するのが3次スプライン。
3次の多項式で表現するため補間式は以下になる。

y=a_i(x-x_i)^3+b_i(x-x_i)^2+c_i(x-x_i)+d_i

補間式の係数$a_i$,$b_i$,$c_i$,$d_i$が求まれば補間値は求まる。サンプルデータ点数が$N+1$点あれば、多項式は$N$個となるので係数は$4N$個、系を閉じるには方程式が$4N$個必要になる。

• サンプルデータ点を必ず通る
• 区間境界点の1次導関数は連続
• 区間境界点の2次導関数は連続

という条件で$4N-2$の方程式が成立する。これにサンプルデータの両端での2次導関数を0とする条件を加えれば$4N$の方程式となる。最後に加えた条件によってスプラインに種別があり、この場合は自然スプラインと呼ばれる。ほとんどの場合自然スプラインが使われるので、3次スプラインと言うと自然3次スプラインと解釈されることが多い。

係数を求めるには$4N$の連立方程式を解く必要があるが、行列表示すると$4N\times 4N$の行列計算となる。ただし、上で挙げた条件によって対角成分とその隣の成分以外が0となり三重対角行列である。三重対角行列はTDMA（Tridiagonal Matrix Algorithm）呼ばれる計算手法で$O(n)$で計算することができる。これのおかげに3次スプラインは普及したと言っても過言ではない（かもしれない）。

こちらもすでに自分が解説するよりわかりやすく解説しているものがたくさんあるので詳細は割愛。
3次スプライン
TDMA-Wikipedia

数値データ処理に用いる自然スプラインに対し、CGで用いられるB-Splineやその一般形でCADで用いられるNURBS（Non-Uniform Rational B-Spline）では必ずしもサンプルデータ点を通らない。

Lagrange Interpolate

ラグランジュの補間多項式を用いる多項式補間。
スプラインとは異なり、区間ではなくサンプルデータ全体から多項式を定める。

計算量（$O(n^2)$）も多く、ルンゲ現象というデメリットもあるのでコレ使うなら3次スプライン使う。ということで詳細も説明も割愛。
ラグランジュ補間-Wikipedia
ルンゲ現象-Wikipedia
ラグランジュ補間公式

Radial Basis Function Interpolate

放射基底関数（Radial Basis Function、RBF）を用いるノンパラメトリックな補間。今回の目玉。というよりこれの検証のがこの記事のメイン。機械学習とかの分野だとRBFネットワークというふうに呼ばれている。

放射基底関数

放射基底関数は「原点からの距離のみに依存する関数」で$\phi(x)$と置くことが多い。けっこういろんな形が提案されている。
代表的なのは

\phi(x)=\|x\|

\phi(x)=exp(-(\epsilon \|x\|)^2)

\phi(x)=\sqrt{1+(\epsilon \|x\|)^2}

\phi(x)=\frac{1}{1+(\epsilon \|x\|)^2}

\phi(x)=\|x\|^k, k=1,3,5,...\\
\phi(x)=\|x\|^k ln(\|x\|), k=2,4,6,...

あたり。
1つ目は線形RBF、2つ目はガウシアンRBF、3つ目は多重二乗RBF、4つ目は逆二乗RBF、5/6つ目は多重調和スプラインRBFと呼ばれる。
ちなみに$\epsilon$で、表現する関数形をどれだけ滑らかにするかを調整できる。$\epsilon$が小さければ距離が大きくなるほどすぐに0に近づき、$\epsilon$が大きいと距離が大きくなってもRBF値が残留するので見た目上、補間関数が滑らかになっていく。

RBFによる補間関数

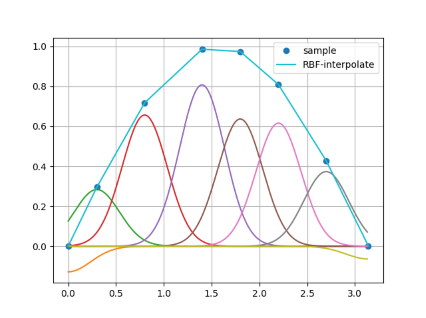
補間にRBFを用いる場合「原点からの距離」の定義は、「Centerと呼ばれる制御点$c$からの距離」となる。複数あるcenterでのRBFを線形結合することで補間関数$f(x)$を生成する。RBF自体はx方向の距離のみに依存するためy方向の数値の大きさを表現しない。そのため各centerでのRBFに重み付けをしてから、線形和をとる。
数式的には

f(x)=\sum_{i=1}^{N}w_i \phi(\|x-x_i\|)

centerをサンプル点とすればcenterの位置$c$は$x_i$となる。$w_i$は各サンプル点での重み。
それらを図式するとこんなイメージ。

パッと見だとサンプル点通ってないじゃないかと思うけど補間関数はこのRBFの総和なのでちゃんとサンプル点は通る。ちなみにこれはガウシアンRBFを用いた場合で、多重二乗RBFとかだともはやプロットしても全然イメージがつかない。

重み付け

重み$w_i$を決めるために補間関数$f(x)$がサンプルデータ点を通るという条件を付する。
$j$番目のサンプルデータ点$x_j$から見て、どのサンプルデータ点をcenterとしてもRBFが$y_j$を通るように重みを決定する形。
数式的には

y_j=\sum_{i=1}^{N}w_i \phi(\|x_j-x_i\|)

これを$N$点のサンプルデータに適用すると$N\times N$の行列となって、まとめると

\left[
  \begin{array}{cccc}
      y_{1} \\
      y_{2} \\
      \vdots \\
      y_{N} 
  \end{array}
\right]
=
\left[
  \begin{array}{cccc}
      w_{1} \\
      w_{2} \\
      \vdots \\
      w_{N} 
  \end{array}
\right]
 \left[
    \begin{array}{cccc}
      \phi(x_1,x_1) & \phi(x_1,x_2) & \ldots & \phi(x_1,x_N) \\
      \phi(x_2,x_1) & \phi(x_2,x_2) & \ldots & \phi(x_2,x_N) \\
      \vdots & \vdots & \ddots & \vdots \\
      \phi(x_N,x_1) & \phi(x_N,x_2) & \ldots & \phi(x_N,x_N) \\
    \end{array}
  \right]

そしてこれは$Y=\Phi W$として線形連立方程式を解くことで重み$w_i$を求めることができる。
逆行列さえ作れれば$W=\Phi ^{-1}Y$として解いてもいいし、直接ガウスの消去法なりで解いてもいい。Pythonならありがたいことにnumpy.linalg.solveが逆行列を介さず解いてくれるので任せれば良し。numpy.linalg.solveの中身はLAPACKの_gesv。

ただ、普通にガウスの消去法を解くとしてLU分解を介して$O(n^2)$にしてもトータルの計算量は$O(n^3)$なので計算は重め。ここまで時間計算量を見ていたけど、サンプル数が増えると空間計算量も重くなりそう。
$O(n^3)$の重みの計算さえ先にやっておければ、補間計算自体は $O(n)$なのでループ内部で重み計算しなければ使い物にはなると思われる。

計算量だけなら3次スプライン圧勝、ただTDMAを実装しないといけないスプラインに対して連立方程式をただ解けばいいだけの実装の容易さは大きい。というかスプライン実装するのが面倒だからRBFが使えるということを検証したい。

関数フィッテング

補間はある$x$の値に対して$y$の値が一意に定まっているデータ群からサンプルのない$x$での$y$の値を推定するもの。
対して、関数フィッテング＝回帰分析はバラツキをもつデータ群からもっともらしい関数形でデータの$x,y$の関連モデルを推定するもの。そもそも用途目的が異なる。所属する団体ではプログラミング難しい(><)的な発想でたくましいExcelシートを組み上げている。Excelシートは数値計算を行うものではない。

(ー_ー;)：Excelシート上だと補間法を組むのは難しい…
( ﾟдﾟ)ﾊｯ!：そや！近似曲線引いてそれから計算すればいいんだ！

用途が違う。

Least Squares Method（最小二乗法）

説明するまでもない。
今回は6次多項式近似を用いる。なぜか？所属する団体で用いられている近似式が全てそれで作られているから。
念の為、scipy.curve_fitとExcelの近似曲線で得られる6項の係数を比較したが一致した。

RBF Fitting

RBF-Interpolateは実験データなどノイズが多いデータで補間行うとものすごい振動する。いわゆる過学習というもの。

過学習に対して、連立方程式を正則化することで耐性を持たせる手法が存在する。理論的なところはあんまり勉強してないけど、数式的には以下。

E=(\Phi W-Y)^2+\Lambda W^2 

\Lambda=
 \left[
    \begin{array}{cccc}
      \lambda & 0 & \ldots & 0 \\
      0 & \lambda & \ldots & 0 \\
      \vdots & \vdots & \ddots & \vdots \\
      0 & 0 & \ldots & \lambda \\
    \end{array}
  \right]

となる評価関数Eが最小化するように重みを決定する。評価関数第1項はサンプルデータ$(x_i,y_i)$と補間関数$f(x_i)$の誤差の自乗和、第2項は方程式の正則化項。評価関数$E$を$W$で偏微分すると最小化において解くべき線形方程式が得られて

(\Phi^\mathrm{T}\Phi+\Lambda)W=\Phi^\mathrm{T}Y

$\lambda$は平滑化パラメータと呼ばれ、$\lambda$を0とすれば点を必ず通る補間状態、$\lambda$を大きくしていくと点は通らず、平均的な曲面を生成できるようになる。

つまり、この正規化手法を用いれば過学習を回避するだけでなくバラツキのあるデータのノンパラメトリックなフィッテングを行うことができる便利な子がRBFということになる。
ただ、用いるRBFや適用データにも依るが、RBF自体のパラメータ$\epsilon$とフィッテングの平滑化パラメータ$\lambda$のバランスが取りづらく、最小二乗法のようにきれいにフィッテングするにはデータに対して細かいパラメータ調整が必要な感触。ツール上で自動でかけるものではなさそう。

比較

• RBF interpolate
• scipy.interpolate.interp1d(kind='cubic')
• scipy.interpolate.interp1d(kind='linear')
• lagrange interpolate
• scipy.optimize.curve_fit

の5つで比較する。

RBF-interpolate

class Interp1dRBF:
    def __radial_basis_function(self, x, c):
        r = np.abs(x - c)
        if self.__rbf_equation == 'gaussian':
            return np.exp(-(self.__eps * r) ** 2)  # Gaussian
        elif self.__rbf_equation == 'multiquadric':
            return np.sqrt(1 + (self.__eps * r) ** 2)  # Multiquadric
        elif self.__rbf_equation == 'inv-quadric':
            return 1.0 / (1 + (self.__eps * r) ** 2)
        elif self.__rbf_equation == 'inv-multiquadric':
            return 1.0 / np.sqrt(1 + (self.__eps * r) ** 2)
        elif self.__rbf_equation == 'thin-plate':
            return r ** 2 * np.log(r)
        elif self.__rbf_equation == 'linear':
            return r
        else:
            print('Error! Not found function=', self.__rbf_equation)
    
    def __weight_solve(self, x, y):
        num = len(x)
        rbf_matrix = np.zeros((num, num))
        for i in range(num):
            for j in range(num):
                rbf_matrix[i, j] = self.__radial_basis_function(x[i], x[j])
        if self.__mode == 'interpolate':
            weights = np.linalg.solve(rbf_matrix, y)
        elif self.__mode == 'fitting':
            weights = np.linalg.solve(rbf_matrix.transpose() * rbf_matrix + self.__lambda * np.identity(num), rbf_matrix.transpose() * y)
        else:
            print('Error! not found interpolate mode=', self.__mode)
            sys.exit()
        return weights

    
    def __init__(self, x_array, y_array, mode='interpolate', rbf='gaussian', eps=1.0, lamda=0.01):
        '''
        '''
        # Error handle
        if len(x_array) != len(y_array):
            print('Error! x-array and y-array must be same length')
            sys.exit()
        self.__x_sample = x_array
        self.__y_sample = y_array
        self.__mode = mode
        self.__rbf_equation = rbf
        self.__eps = eps
        self.__lambda = lamda
        self.__weights = self.__weight_solve(self.__x_sample, self.__y_sample)
        ## plot RBFs
        # for i in range(len(self.__x_sample)):
        #     x = self.__x_sample[i]
        #     w = self.__weights[i]
        #     x_phi = np.arange(np.min(self.__x_sample), np.max(self.__x_sample), 0.01)
        #     y_phi = w * self.__radial_basis_function(x_phi, x)
        #     plt.plot(x_phi, y_phi)

    def __interpolate(self, x_input):
        rbf = self.__radial_basis_function(x_input, self.__x_sample)
        y_inter = np.sum(self.__weights * rbf)
        return y_inter

    def __call__(self, x):
        if type(x) is str:
            return self.__interpolate(float(x))
        elif type(x) in (int, float):
            return self.__interpolate(x)            
        elif type(x) is list or type(x).__module__ == np.__name__:
            return np.array([self.__interpolate(x_input) for x_input in x])
        else:
            print('Error! must be calulatable object')
            print('input:', type(x))
            sys.exit()

githubで公開してるコードと同一。

lagrange-interpolate

class Lagrange:
    def __init__(self, x, y):
        self.xx = x
        self.yy = y

    def __call__(self, x):
        y = 0.0
        for i in range(len(self.xx)):
            up = 1.0
            down = 1.0
            for k in range(len(self.xx)):
                if k == i:
                    pass
                else:
                    up *= (x - self.xx[k])
                    down *= (self.xx[i] - self.xx[k])
            y += self.yy[i] * up / down
        return y

精度

y=sin(x)

まずパラメトリックな関数での精度比較。
関数として$y=\sin(x)$でやってみる。サンプル点として0から2.1$\pi$を0.25刻みで用意する。
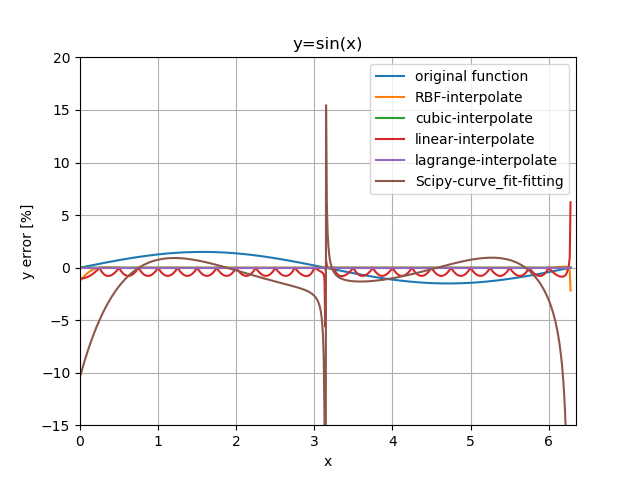
サンプル点と補間結果のプロット。

誤差プロット。

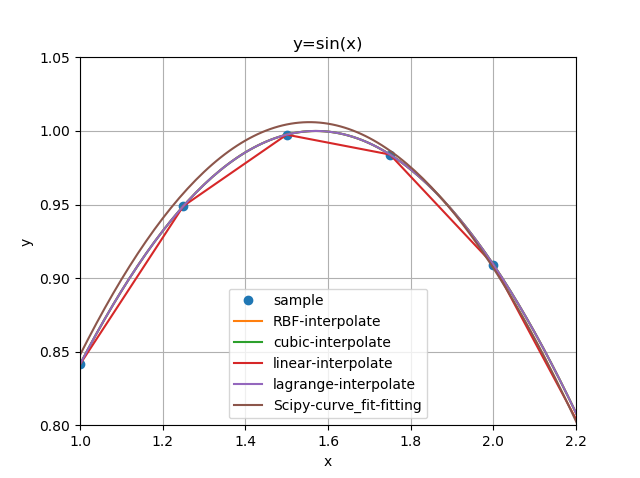
Lagrangeはルンゲ現象さえ起こさなければさすがの精度。次いで3次スプライン。
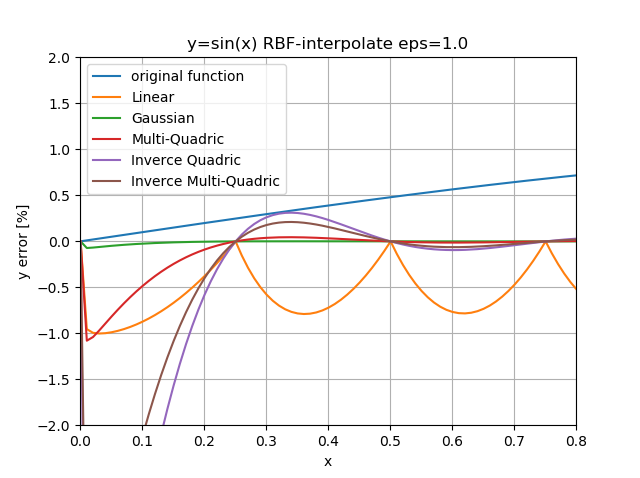
Linearは期待通りサンプル点を通りつつ、それ以外では精度が出ない。
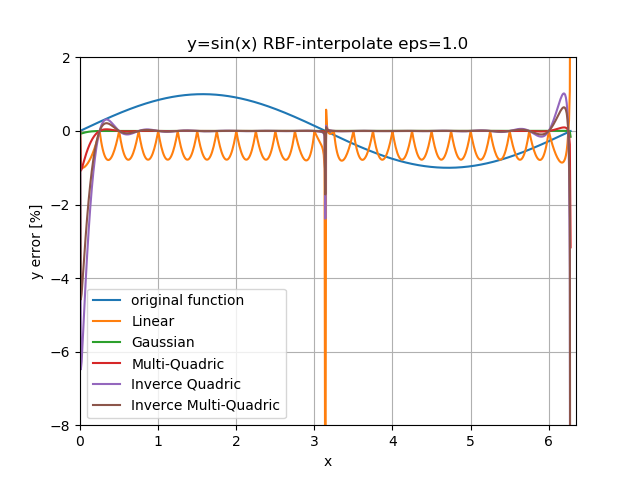
RBFが思ったよりオーバーシュートしている。

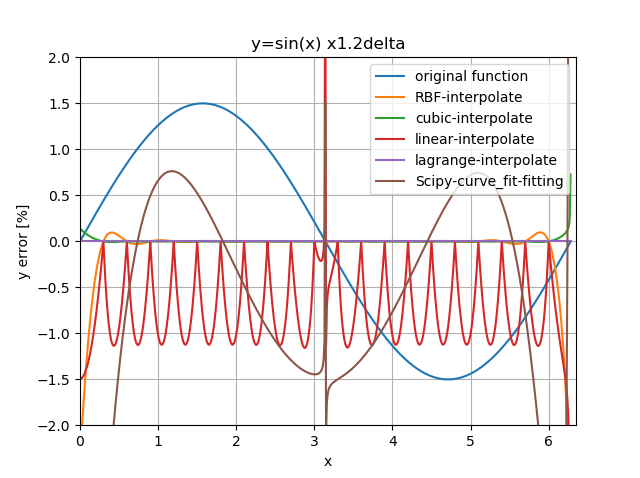
サンプル点数を増減させてみた結果も。刻みを0.25から1.2倍したものと0.8倍したもの。

傾向は変わらず、誤差が減っている。スプライン、RBFともにサンプル点数が増えればオーバーシュートは抑制できる。
0.8倍でもlagrangeはルンゲ現象を起こしていない。0.5倍あたりから起こり始め0.4倍でダメになった。意外とルンゲ現象が起きるしきい値が高いのかもしれない。

最小二乗法フィッテング結果は、所属団体の皆様にはぜひこれを見せて改心を勧めたい。といった感想。

RBFの関数形比較

と、実はここまでのRBF補間は多重二乗RBFで$\epsilon=1.0$を用いていた。もちろんこれらを変更すれば結果も変わってくるので、ここでRBFでの種類別の比較を行う。

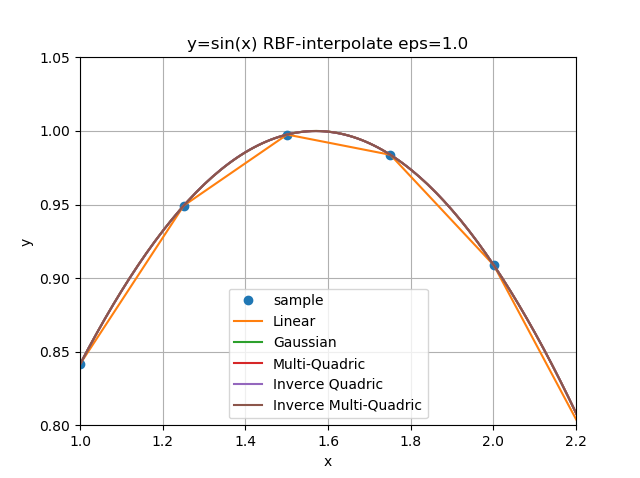
まず、$\epsilon$を1.0に固定して関数形状での比較。

なんだか線形RBFは線形補間と同じような感触。
オーバーシュートが小さい順は ガウシアン < 多重二乗 < 逆多重二乗 < 逆二乗。
知人からオススメしていただいたのは多重二乗だったのだけれど、ガウシアン優勢？

次に$\epsilon$を5.0まで上げてみる。


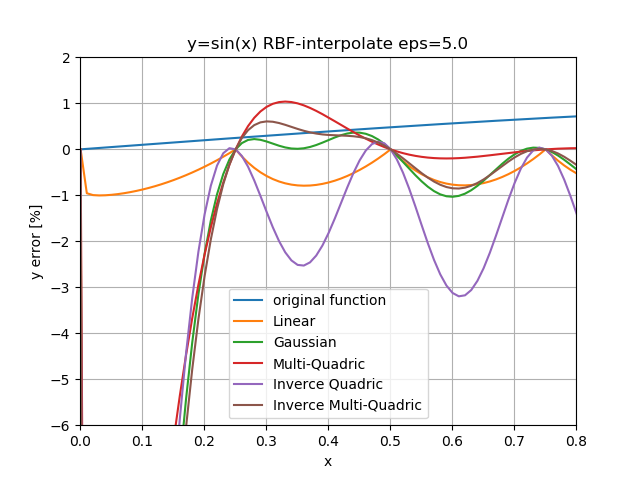
線形RBFは$\epsilon$を変えてもあまり変化なし。
オーバーシュートは多重二乗が大きいものの大差はなく、他は不穏な様子。

思い切って$\epsilon$を10.0まで引き上げてみる。

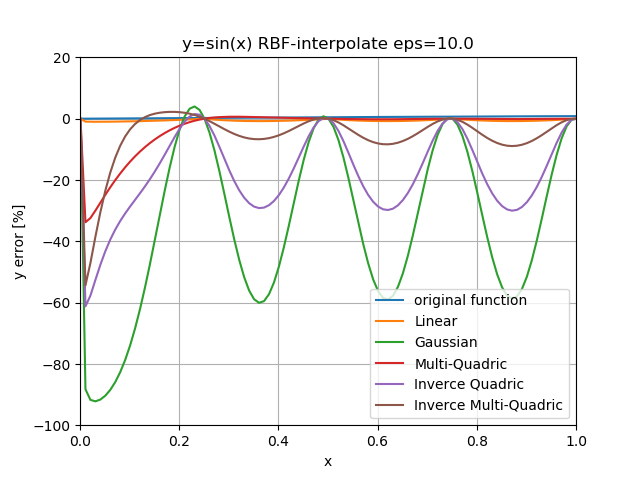
$\epsilon$の影響がかなり大きいことがよーくわかる。
線形RBFはやはり影響あまりなし。
多重二乗RBF以外は使用に堪えない様子。多重二乗RBFは安定していると言えるのかもしれない。

逆に$\epsilon$小さくしてみる。0.1。


$\epsilon$を小さくしたので全体的に誤差は小さくなっているが、関数がカクついている感触。
ガウシアンRBFが白色雑音を混ぜたようなノイズを持ってしまっている。線形RBFは相変わらず。

適切な$\epsilon$を選択できればガウシアンRBFが優秀だが、$\epsilon$の感度が大きい。データによって適切な$\epsilon$が変化することを考えると使いにくさが勝る。そういう意味では多重二乗RBFが$\epsilon$の感度が小さく、ある程度$\epsilon$を決めおいて埋め込んでおいても実用できそう。

一応$\epsilon$での比較。

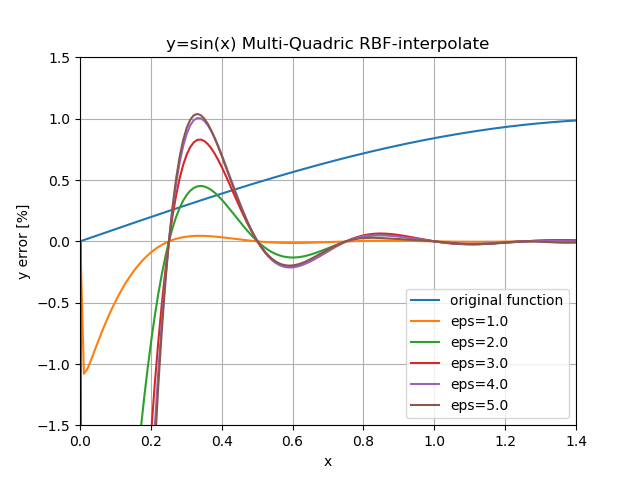
$y=\sin(x)$では$\epsilon\le1$が良い模様。

ノンパラメトリックデータの補間

実際に使うのはノンパラメトリックなデータの補間なのでそちらでの結果を見る。
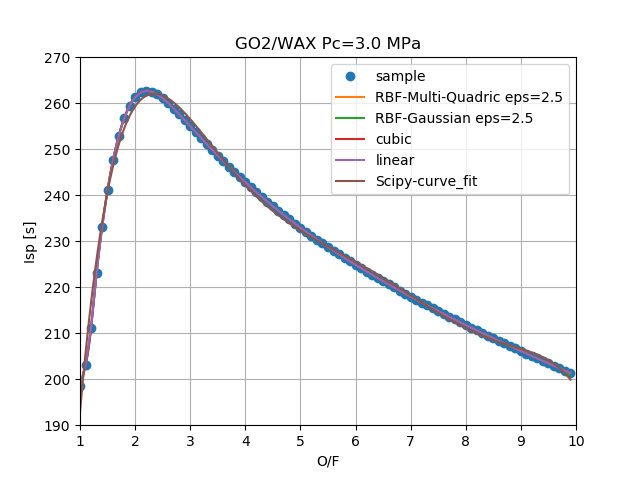
使うのはロケットエンジンにおけるO/F（酸化剤と燃料の比率）とIsp（すごくざっくり言うとロケットエンジンの性能）のデータ。
O/Fは設計される値で、IspはO/F含め複数のパラメータを使って化学平衡計算で求められる。

Lagrangeは、プロットしているサンプルではルンゲ現象が顕著となり、ルンゲ現象が起きない程度に粗くしたサンプルでは比較に必要な精度を得られなかったため除外している。

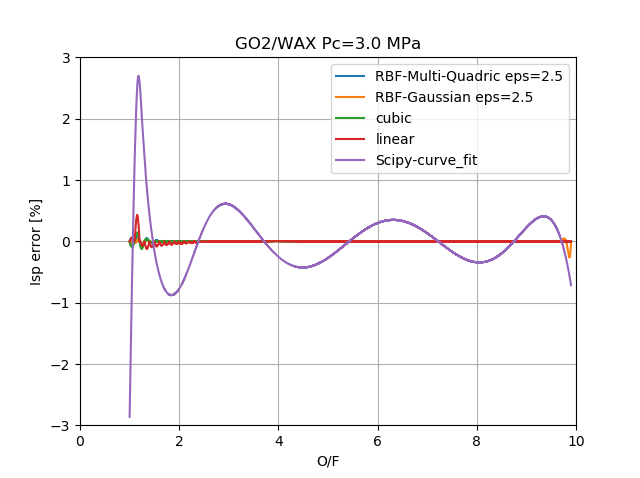
驚くべきことに$\epsilon$さえしっかり調整してやるとRBFが3次スプラインを超える精度を出せていることがわかる。逆に言えば$\epsilon$を調整しないと3次スプラインのほうが良いということでもある。

最小二乗法フィッテング結果は、所属団体の皆様にはぜひこれを見せて改心を(ry
というかこんな精度で設計してもいいのだろうか？？と思わざるを得ない結果。たかが1%されど1%。
普段、効率が1%が上下すればかなりインパクトがある値なのだが。

計算量

各補間手法での時間計算量を比較する。
ただし、実装に大きく左右される面もあるため参考程度。

補間時間

まず、補間器が作成されている状態での補間の計算量を見てみる。
データ数に対する経過時間でプロットした。lagrangeに関しては上記のコードから$O(n^2)$であることが明らかなので除外している。
1回の補間ではオーダーが小さいので、補間10000回を5セット行い5セットの時間を平均化。

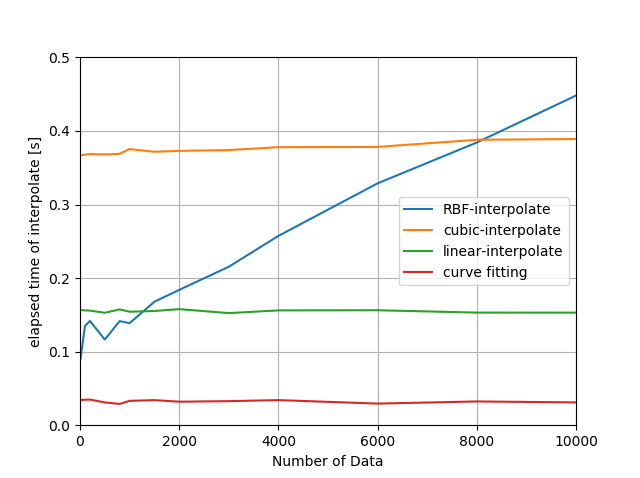
RBFが$O(n)$、それ以外が$O(1)$という結果。緩いがスプラインは$O(n)$になっている？
RBFとフィッティングに関しては上記コードの実装的にも計算量オーダーは妥当。linearとスプラインは予想外。計算量ってforがどれだけまわるかというよりforの内部での計算処理回数なんですかね。それならxのサーチは計算量には含まれないので$O(1)$は妥当？

Scipyに実装されてる2つの子、linearとスプラインはおおよそ2倍くらいの差。linearで15$\mu$s/回、スプラインで40$\mu$s/回程度。補間回数増えれば差が広がりそう。以前スプラインで補間しているとまったく終わらない解析がlinearだとすんなり終わった経験も納得の数字。とりあえずサンプル数8000まではRBFでもスプラインより軽いことはわかった。

補間器作成時間

次に補間器の作成計算量を見る。
RBFは$O(n^3)$であるのが予想されるので5回作成して平均化。
その他は100回作成を5セットで平均化。

RBFが$O(n^3)$なのが確認された。スプラインもTDMAのおかげで$O(n)$になっている。

実際の動かし方（補間器作成=>補間）

最後に補間器の作成と補間のセットでの計算量を見る。
補間器を作成して10000回の補間を5セットで平均化。


やはりRBFの$O(n^3)$が効く。

まとめ

スプラインの実装を避けたくて、楽に実装できるRBFをつまみ食いしてみた。
Scipyが優秀すぎてスプラインで困ることがまったくない状態であることが改めて確認された。Pythonで解析している間はScipy.interpolateのcubicに頼るのが安定して結果を得られる。
自分で実装したスプラインとそのうち比較してみようと思う。